绪论
-
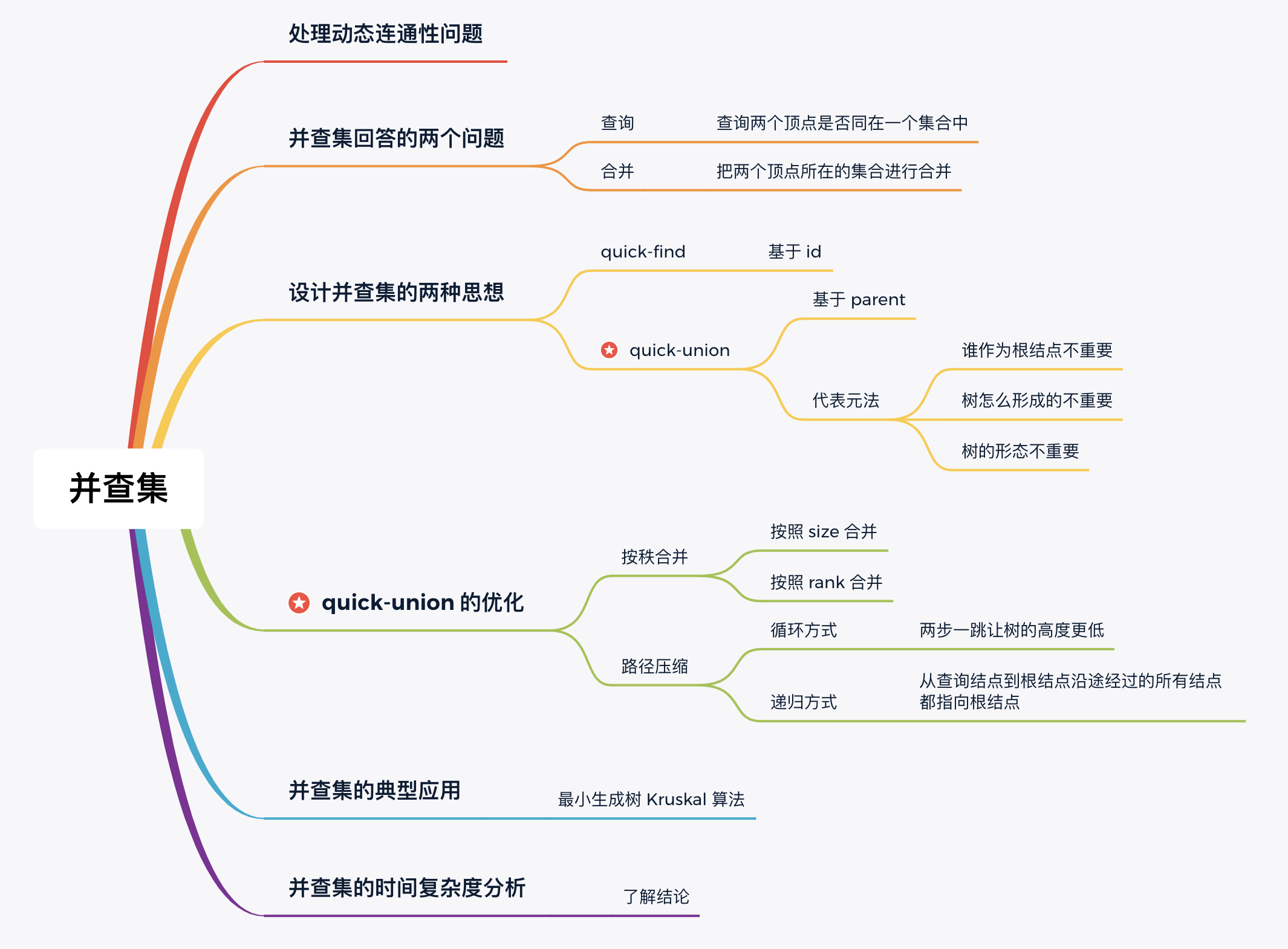
(Union Find)也叫「不相交集合(Disjoint Set)。专门用于 动态处理 不相交集合的「查询」与「合并」问题。
-
可以使用并查集的问题一般都可以使用基于遍历的搜索算法(深度优先搜索DFS、广度优先搜索BFS)完成,但是使用并查集会使得解决问题的过程更加清晰、直观。
-
并查集的主要作用是解决网络的连通性。这里的网络可以是计算机网络,也可以是人际关系的网络。例如:我们可以通过并查集判断两个人是否来自同一个祖先。
-
常用术语
- 父节点:顶点的直接父亲节点。没有父亲的节点的父节点是其本身。
- 根节点:一棵树的根节点。没有父节点的节点的根节点是其本身。
理论知识
A 并查集动态处理的两个问题:
-
查询(Find):查询图中的两个顶点是不是在同一个集合中。
注意:并查集只回答两个顶点之间是否有一条路径连接,而不回答怎么连接。
-
合并(Union):将两个不相交集合进行合并。
B 两种思想:
- 「基于 id」的思想给每一个元素(顶点)分配一个唯一标识,称为
id。基于id的做法很少见,了解即可。 - 「基于 parent」的思想:记录每个顶点的父亲顶点是谁。这样设计「并查集」的思想也叫「代表元」法。
parent数组的定义是:parent[i]表示标识为i的结点的父亲结点的标识(可以形象地记为「找爸爸」)。在这个定义下,根结点的父亲结点是自己。因此,这种方式形成的「并查集」组织成了 若干个不相交的树形结构,并且我们在访问结点的时候,总是按照「从下到上」进行访问的。
C 代表元法:
-
三个不重要
- 谁作为根结点不重要:根结点与非根结点只是位置不同,并没有附加的含义;
- 树怎么形成的不重要:合并的时候任何一个集合的根结点指向另一个结合的根结点就可以;
- 树的形态不重要:理由同「谁作为根结点不重要」。
-
个人理解:重要的是确定元素a和元素b是不是同一个集合!谁当代表无所谓。
-
可能造成的问题:树的高度过高,查询性能降低。
-
其实几乎所有树状的算法都会和树的高度较劲:
- 「快速排序」,使用随机化
pivot的方式避免递归树太深; - 「二叉搜索树」为了避免递归树太深,采用不同的旋转方式,得到了 AVL 树和红黑树。
- 「快速排序」,使用随机化
-
而解决方案有「按秩合并」与「路径压缩」。
D 按秩合并
按「秩」合并的意思是:让树的「秩」较小的树的根结点,指向树的「秩」较大的树的根结点。这里的「秩」有两种含义,分别用于不同的场景:
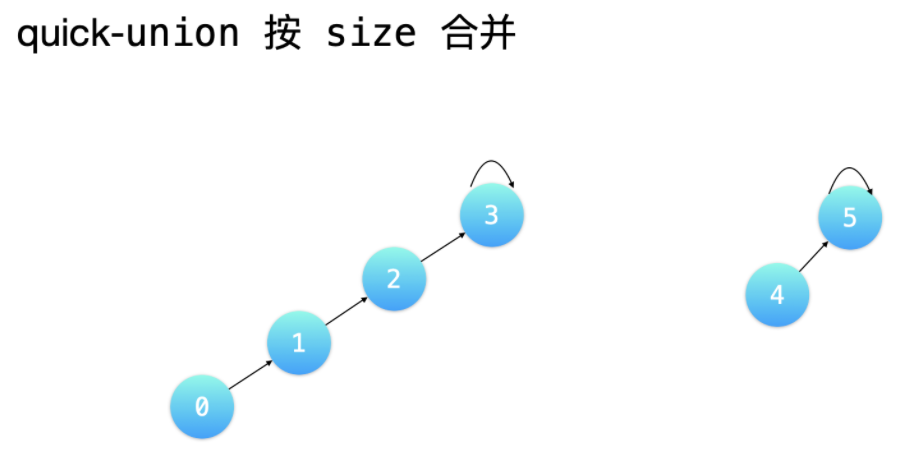
- 按 size 合并,用于需要维护每个连通分量结点个数的时候;
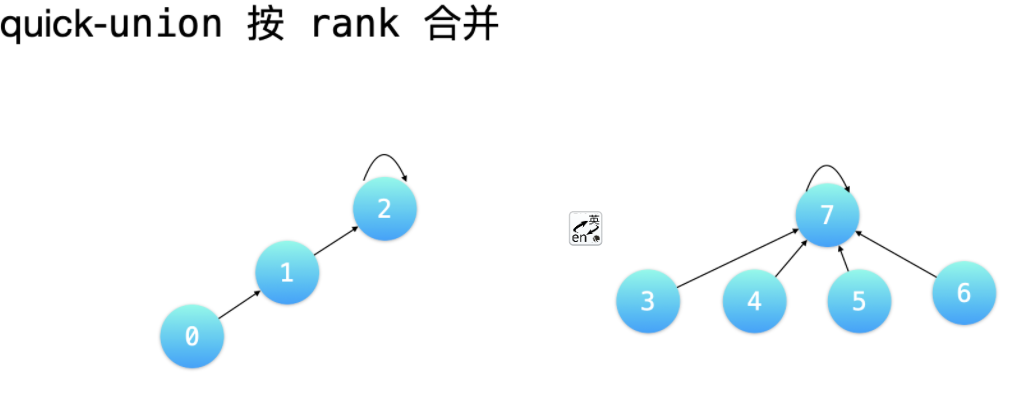
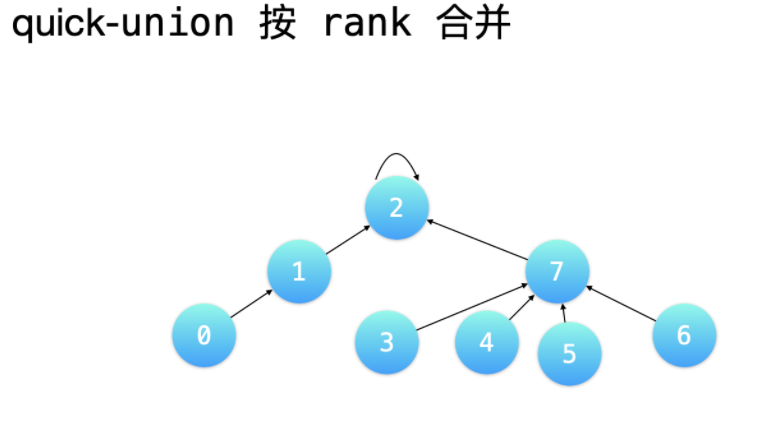
节点总数 - 按 rank 合并,绝大多数时候。
树的高度
-
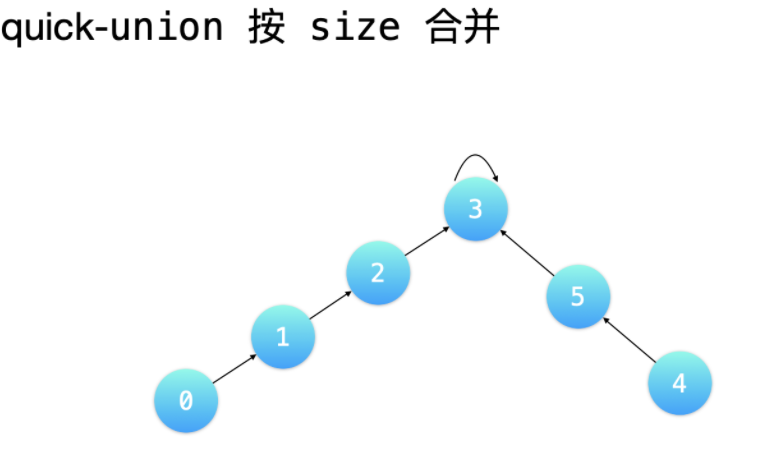
按
size合并的意思是让树的「结点总数」较小的树的根结点,指向树的「结点总数」较大的树的根结点。 -
-
按
rank合并的意思是让树的「高度」较小的树的根结点,指向树的「高度」较大的树的根结点。 -
E 路径压缩
-
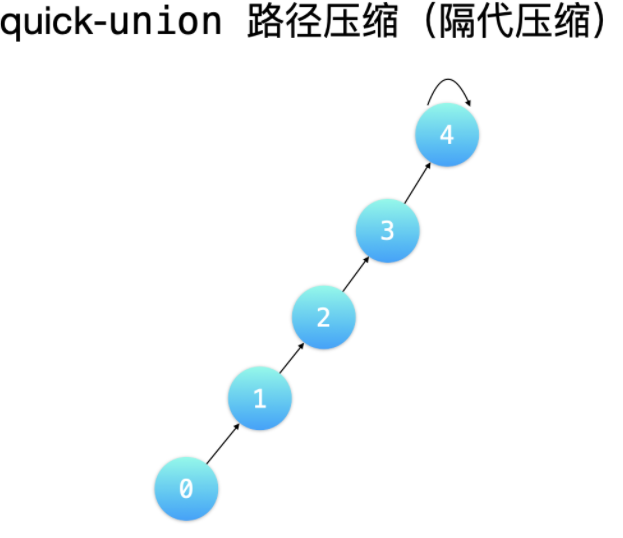
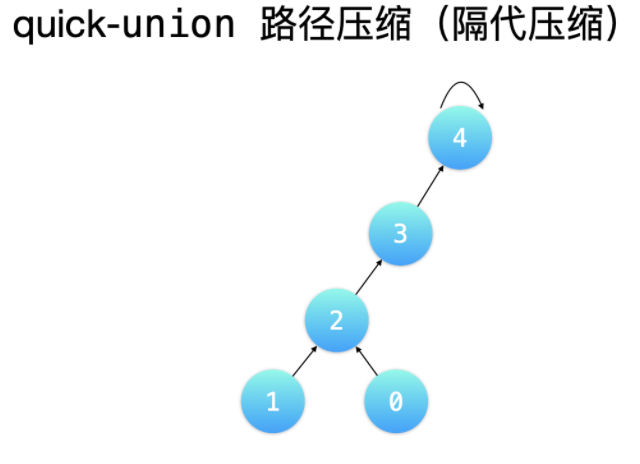
路径压缩方式 1:隔代压缩
「隔代压缩」的意思是:两步一跳,一直循环执行「把当前结点指向它的父亲结点的父亲结点」这样的操作。这样的压缩并不彻底,但是多压缩几次,就可以达到压缩彻底的效果。
-
-
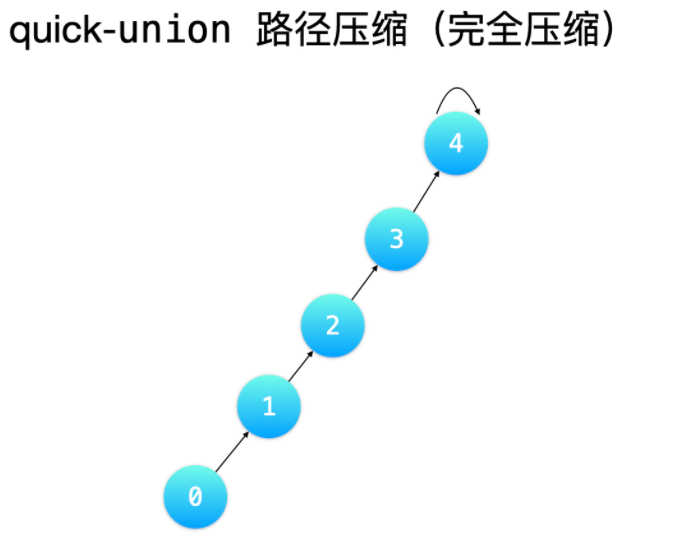
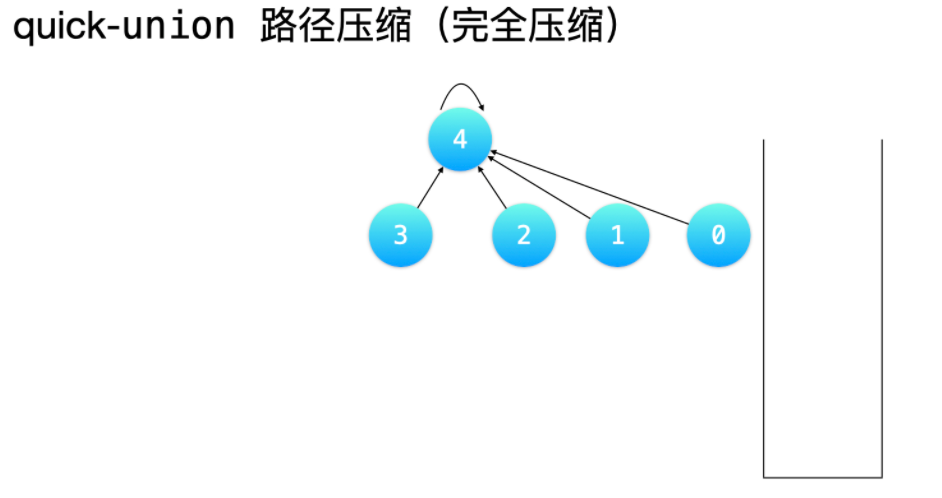
路径压缩方式 2:完全压缩
「完全压缩」的意思是:把从「查询结点」到「根结点」沿途经过的所有结点都指向根结点。相较于「隔代压缩」,「完全压缩」压缩得更彻底。——使用栈这种结构,很容易实现。
-
F 时间复杂度分析
-
并查集的时间复杂度分析,其理论性较强,通常只需要知道结论即可。这里我们给出结论:
同时使用按秩合并与路径压缩时,最坏情况的时间复杂度为 $O(m\alpha(n))$,这里$\alpha(n)$是一个增长非常慢的函数,$\alpha(n)<4$。
-
由于路径压缩采用「一边查询,一边修改树结构」的策略,并且 修改树的结构是不可逆的,合并之前需要先查询再合并。如果次数非常多的话,最后并查集里所有的树的高度都只有 22,平均到每一次「合并」和「查询」操作,步骤是常数次的。
基本思想:代表元
-
解决节点之间是否连接的问题,包括直接连接和间接连接。
-
如果给你一些顶点,并且告诉你每个顶点的连接关系,你如何才能快速的找出两个顶点是否具有连通性呢?如「下图 的连通性问题」,该图给出了顶点与顶点之间的连接关系,那么,我们如何让计算机快速定位 (0, 3) , (1, 5), (7, 8) 是否相连呢?此时我们就需要机智的「并查集」数据结构了。
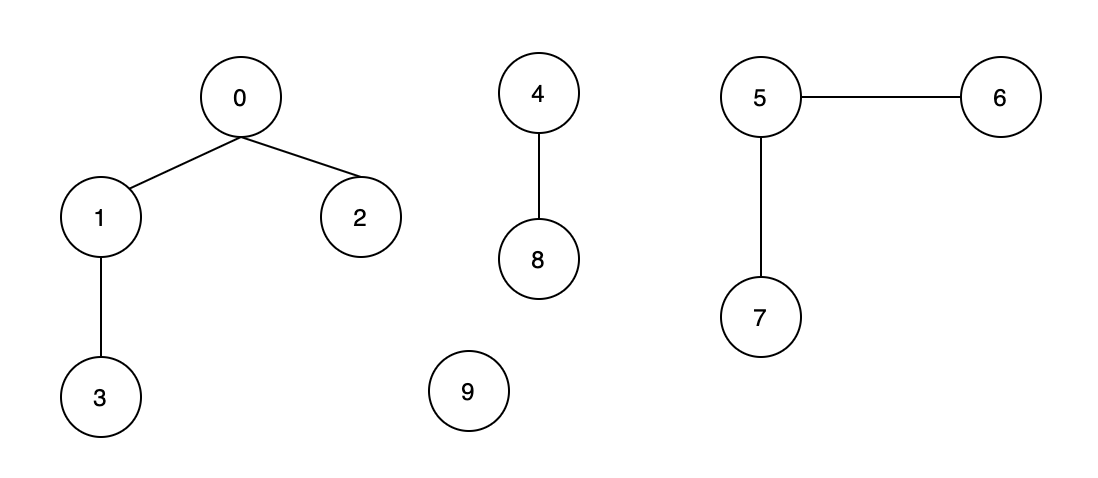
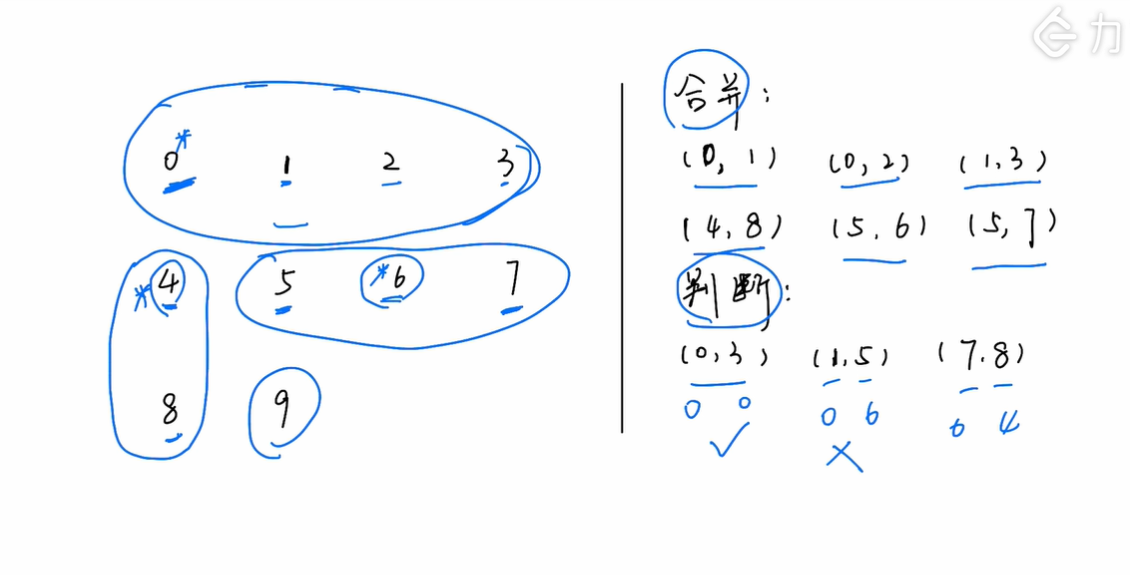
上图(0,1,2,3)的代表是0,(4,8)的代表是4,(5,6,7)的代表是5,(9)的代表是9。根据代表是否相同进行判别是否连通。
以上就是代表元法的本质。
并查集模板
-
采用数组——路径压缩采用——完全压缩
-
重点是Find和Union函数怎么写
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30//定义并查集类 class UnionFind{ public: vector<int> parent;//父节点 //构造函数 UnionFind(){ parent.resize(26); //每一个小写字母的父节点都是自己 iota(parent.begin(), parent.end(), 0); } //递归寻找返回父亲id int Find(int idx){ //如果是根节点,直接返回 if(idx==parent[idx]){ return idx; } //递归查找,同时更新父节点, 动态压缩最后树的高度只是2 parent[idx]=Find(parent[idx]); return parent[idx]; } //合并父节点,以等号后面的变量为新的根节点 void Union(int idx1, int idx2){ int newroot=Find(idx2); //找到idx1的最高的父亲节点,从下往上 parent[Find(idx1)]=newroot; } }; -
也可以有Union函数按秩合并的优化

-
connected函数的定义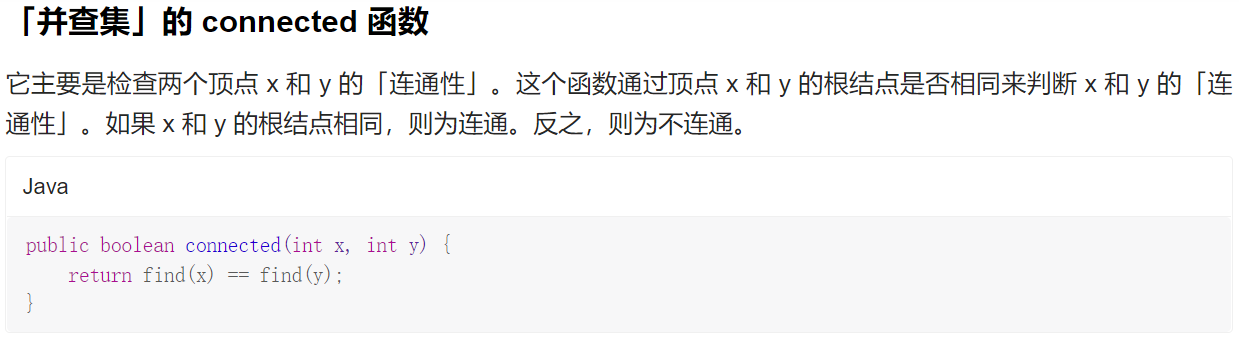
基本问题选讲
-
给定一个由表示变量之间关系的字符串方程组成的数组,每个字符串方程
equations[i]的长度为4,并采用两种不同的形式之一:"a==b"或"a!=b"。在这里,a 和 b 是小写字母(不一定不同),表示单字母变量名。只有当可以将整数分配给变量名,以便满足所有给定的方程时才返回
true,否则返回false。 -
思路:
-
我们可以将每一个变量看作图中的一个节点,把相等的关系 == 看作是连接两个节点的边,那么由于表示相等关系的等式方程具有传递性,即如果
a==b和b==c成立,则a==c也成立。也就是说,所有相等的变量属于同一个连通分量。因此,我们可以使用并查集来维护这种连通分量的关系。 -
首先遍历所有的等式,构造并查集。同一个等式中的两个变量属于同一个连通分量,因此将两个变量进行合并。然后遍历所有的不等式。同一个不等式中的两个变量不能属于同一个连通分量,因此对两个变量分别查找其所在的连通分量,如果两个变量在同一个连通分量中,则产生矛盾,返回 false。如果遍历完所有的不等式没有发现矛盾,则返回 true。
-
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61//定义并查集类 class UnionFind{ public: vector<int> parent;//父节点 //构造函数 UnionFind(){ parent.resize(26); //每一个小写字母的父节点都是自己 iota(parent.begin(), parent.end(), 0); } //递归寻找返回父亲id int Find(int idx){ //如果是根节点,直接返回 if(idx==parent[idx]){ return idx; } //递归查找,同时更新父节点, 动态压缩最后树的高度只是2 parent[idx]=Find(parent[idx]); return parent[idx]; } //合并父节点,以等号后面的变量为新的根节点 void Union(int idx1, int idx2){ int newroot=Find(idx2); //找到idx1的最高的父亲节点,从下往上 parent[Find(idx1)]=newroot; } }; class Solution { public: bool equationsPossible(vector<string>& equations) { UnionFind uf; //第一遍遍历等号,重新合并 for(auto &i:equations){ if(i[1]=='='){ int idx1=i[0]-'a'; int idx2=i[3]-'a'; uf.Union(idx1, idx2); } } //第二次判断查找 for(auto &i:equations){ if(i[1]=='!'){ int idx1=i[0]-'a'; int idx2=i[3]-'a'; int par1=uf.Find(idx1); int par2=uf.Find(idx2); if(par1==par2){ return false; } } } return true; } };
-
-
有
n个城市,其中一些彼此相连,另一些没有相连。如果城市a与城市b直接相连,且城市b与城市c直接相连,那么城市a与城市c间接相连。省份 是一组直接或间接相连的城市,组内不含其他没有相连的城市。
给你一个
n x n的矩阵isConnected,其中isConnected[i][j] = 1表示第i个城市和第j个城市直接相连,而isConnected[i][j] = 0表示二者不直接相连。返回矩阵中 省份 的数量。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40class Solution { public: //找最高的根节点 int Find(vector<int> &parent, int idx){ if(parent[idx]==idx){ return idx; } //递归查询,并更新 parent[idx]=Find(parent,parent[idx]); return parent[idx]; } //合并,默认idx2为根节点 void Union(vector<int> &parent, int idx1, int idx2){ int newroot=Find(parent,idx2); parent[Find(parent,idx1)]=newroot; } int findCircleNum(vector<vector<int>>& isConnected) { int n=isConnected.size();//城市数量 //初始化父亲节点 vector<int> parent(n); iota(parent.begin(),parent.end(),0); //遍历半三角即可,合并 for(int i=0;i<n;++i){ for(int j=i+1;j<n;++j){ if(isConnected[i][j]==1){ Union(parent,i,j); } } } int ret=0; for(int i=0;i<parent.size();++i){ if(parent[i]==i) ++ret; } return ret; } }; -
树可以看成是一个连通且 无环 的 无向 图。
给定往一棵
n个节点 (节点值1~n) 的树中添加一条边后的图。添加的边的两个顶点包含在1到n中间,且这条附加的边不属于树中已存在的边。图的信息记录于长度为n的二维数组edges,edges[i] = [ai, bi]表示图中在ai和bi之间存在一条边。请找出一条可以删去的边,删除后可使得剩余部分是一个有着
n个节点的树。如果有多个答案,则返回数组edges中最后出现的边。-
思路:

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35class Solution { public: int Find(vector<int> &parent, int idx){ if(idx==parent[idx]){ return idx; } //动态更新 parent[idx]=Find(parent, parent[idx]); return parent[idx]; } //默认已idx2为主 void Union(vector<int> &parent, int idx1, int idx2){ int newroot=Find(parent,idx2); parent[Find(parent,idx1)]=newroot; } vector<int> findRedundantConnection(vector<vector<int>>& edges) { int n=edges.size(); vector<int> parent(n); //注意父亲id和数组索引的关系 iota(parent.begin(),parent.end(),0); //遍历 for(auto &i:edges){ int idx1=i[0]-1; int idx2=i[1]-1; if(Find(parent, idx1)!=Find(parent,idx2)){ Union(parent, idx1, idx2); }else{ return i; } } return vector<int>{}; } }; -
-
用以太网线缆将
n台计算机连接成一个网络,计算机的编号从0到n-1。线缆用connections表示,其中connections[i] = [a, b]连接了计算机a和b。网络中的任何一台计算机都可以通过网络直接或者间接访问同一个网络中其他任意一台计算机。
给你这个计算机网络的初始布线
connections,你可以拔开任意两台直连计算机之间的线缆,并用它连接一对未直连的计算机。请你计算并返回使所有计算机都连通所需的最少操作次数。如果不可能,则返回 -1 。 -
思路:
-
当计算机的数量为
n时,我们至少需要n-1根线才能将它们进行连接。如果线的数量少于n−1,那么我们无论如何都无法将这n台计算机进行连接。因此如果数组connections的长度小于 n-1,我们可以直接返回 -1作为答案,否则我们一定可以找到一种操作方式。 -
那怎么计算最少的操作数目呢。使用并查集计算连通分量的个数
n1,在这个过程计算冗余的连线的个数n2,如果n1-1>n2,那必然这些连通分量是连不在一起的,直接返回-1,否则返回n1-1的数量。 -
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44class Solution { public: int Find(vector<int> &parent, int idx){ if(parent[idx]==idx){ return idx; } parent[idx]=Find(parent, parent[idx]); return parent[idx]; } void Union(vector<int> &parent, int idx1, int idx2){ int newroot=Find(parent,idx2); //修改最高的父母节点 parent[Find(parent,idx1)]=newroot; } int makeConnected(int n, vector<vector<int>>& connections) { vector<int> parent(n); iota(parent.begin(),parent.end(),0); int count=0;//冗余连接 int group=0;//连通个数 for(auto &i:connections){ int idx1=i[0]; int idx2=i[1]; int par1=Find(parent, idx1);//主动更新一次 int par2=Find(parent,idx2); if(par1==par2){ ++count; }else{ Union(parent, idx1, idx2); } } for(int i=0;i<n;++i){ if(parent[i]==i){ ++group; } } if((group-1)>count){ return -1; }else{ return group-1; } } };
-
-
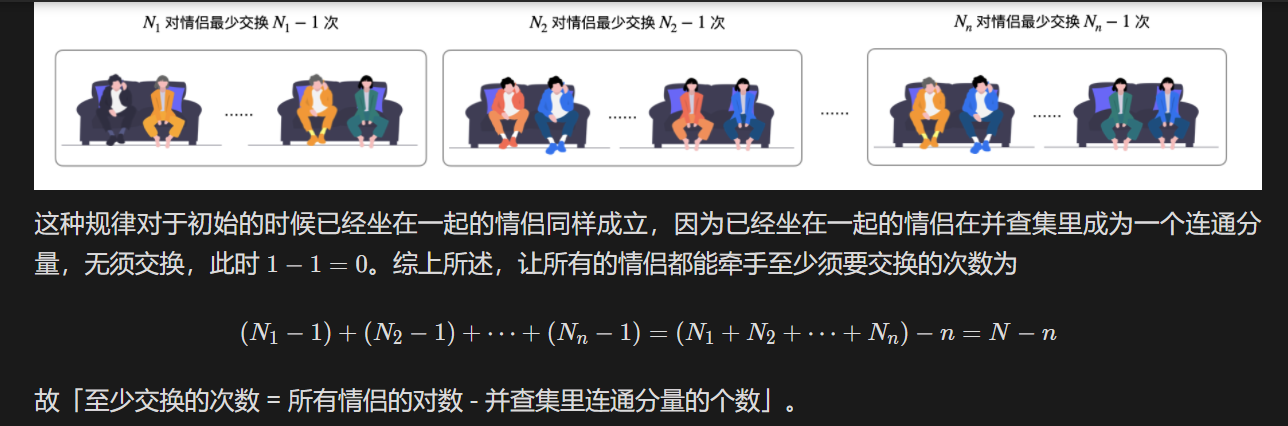
n对情侣坐在连续排列的2n个座位上,想要牵到对方的手。人和座位由一个整数数组
row表示,其中row[i]是坐在第i个座位上的人的 ID。情侣们按顺序编号,第一对是(0, 1),第二对是(2, 3),以此类推,最后一对是(2n-2, 2n-1)。返回 最少交换座位的次数,以便每对情侣可以并肩坐在一起。 每次交换可选择任意两人,让他们站起来交换座位。
-
难点:和连通分量合在一起。
-
思路:
-

-
-
-
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47class Solution { public: int Find(vector<int> &parent, int idx){ if(parent[idx]==idx){ return idx; } //更新 parent[idx]=Find(parent,parent[idx]); return parent[idx]; } void Union(vector<int> &parent, int idx1, int idx2){ int newroot=Find(parent,idx2); parent[Find(parent,idx1)]=newroot; } int minSwapsCouples(vector<int>& row) { int len =row.size(); int n=len/2; vector<int> parent(n);//n对 iota(parent.begin(), parent.end(), 0); for(int i=0;i<len;i+=2){ //注意是row[i],然后还要除以2,这是难点,因为2、3分别/2结果是一样的 int idx1=row[i]/2; int idx2=row[i+1]/2; //更新一次 int par1=Find(parent, idx1); int par2=Find(parent, idx2); if(par1==par2){ continue; }else{ //合并连通分量 Union(parent, idx1, idx2); } } //计算连通分量个数 int div=0; for(int i=0;i<n;++i){ if(parent[i]==i){ ++div; } } return n-div; } };
进阶问题选讲
-
给你一个整数数组
nums和一个整数threshold。找到长度为
k的nums子数组,满足数组中 每个 元素都 大于threshold / k。请你返回满足要求的 任意 子数组的 大小 。如果没有这样的子数组,返回
-1。子数组 是数组中一段连续非空的元素序列。
-
思路1:排序+并查集。按大小排序,但要保持本来的idx下标来合并。
-
并查集,并且不需要枚举k。排序后从大到小依次加入元素,那刚刚加入的元素必定是最小元素,最小元素就是木桶里面最短的木板,所以只需要根据最小元素的大小反推出k。子数组的长度当然是多多益善,而并查集可以知道这个连通块的大小。
-
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76class UnionFind{ public: vector<int> Fa;//父亲, 数组下标 vector<int> Sz;//长度 UnionFind(int n){ //规定都从1开始,0无效 Fa.resize(n+1); Sz.resize(n+1,1); iota(Fa.begin() , Fa.end(), 0); } int Find(int idx){ if(idx == Fa[idx]){ return idx; } Fa[idx] = Find(Fa[idx]); return Fa[idx]; } //合并,以长度最长的为集合代表,统一标准 void Merge(int idx1, int idx2){ int x = Find (idx1), y = Find (idx2); if(x==y){ return; } //保证x的长度最长,为集合代表 if (Sz[x] < Sz[y]) swap (x, y); Fa[y] = x;//更改代表 Sz[x] += Sz[y];//更改长度 } //返回合并的长度 int Size(int idx){ int x = Find(idx); return Sz[x]; } }; class Solution { public: int validSubarraySize(vector<int>& nums, int threshold) { int n = nums.size(); UnionFind uf(n); bool visited[n+1];//判断元素是否读取了 vector<pair<int,int>> curr; //注意序号都从1开始 for(int i =0;i<n;++i){ visited[i+1] = false; curr.push_back(pair<int,int>{nums[i],i+1}); } sort(curr.begin(),curr.end(),[](auto &i,auto &j)->bool{ return i.first>j.first; }); //依次从最大开始向最小读起,这也是为什么要从1开始的原因,可以直接计算长度 //大的开始满足,不满足就增加长度减少阈值。遍历一遍都不满足,就不可以 for(auto &j:curr){ int idx = j.second; //连接后面 if(idx+1<=n && visited[idx+1]){ uf.Merge(idx, idx+1); } //连接前面 if(idx-1>0 && visited[idx-1]){ uf.Merge(idx, idx-1); } visited[idx] = true; int len = uf.Size(idx); if((long)len*j.first>threshold){ return len; } } return -1; } }; -
思路2:单调栈:可以想象,子数组长度越长,每个元素的值要求就越小。所以,针对每个元素,求出其左右比该元素少的边界,可以枚举所有元素的最好情况,如果这些情况都不满足,就不可能存在该数组。
-
如何求取比该值左右边界,使用单调栈求取。
-
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32class Solution { public: //使用单调栈 int validSubarraySize(vector<int>& nums, int threshold) { int n = nums.size(); int left[n];//比当前元素少的最近左边界,最左为-1 int right[n];//比当前元素少的最近右边界,最右为n stack<int> s; for(int i=0;i<n;++i){ while(!s.empty() && nums[s.top()]>=nums[i]){ s.pop(); } left[i] = s.empty()?-1:s.top(); s.push(i); } s = stack<int>();//清空栈 for(int i=n-1;i>=0;--i){ while(!s.empty() && nums[s.top()]>=nums[i]){ s.pop(); } right[i] = s.empty()?n:s.top(); s.push(i); } //开始计算 for(int i =0;i<n;++i){ if((long)nums[i]*(right[i]-left[i]-1)>threshold){ return right[i]-left[i]-1; } } return -1; } }; -
给定一个由不同正整数的组成的非空数组
nums,考虑下面的图:- 有
nums.length个节点,按从nums[0]到nums[nums.length - 1]标记; - 只有当
nums[i]和nums[j]共用一个大于 1 的公因数时,nums[i]和nums[j]之间才有一条边。
返回 图中最大连通组件的大小 。
- 有
-
思路1:辗转相除计算最大公约数建图+BFS求连通分量个数。超时
-
思路2:枚举因式+并查集
-
默认都以最小因数为代表元
-
-
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56class UnionFind { public: UnionFind(int n) { parent = vector<int>(n); for (int i = 0; i < n; i++) { parent[i] = i; } } void uni(int x, int y) { int rootx = find(x); int rooty = find(y); if (rootx != rooty) { //以最小的因式作为代表 if(rootx>rooty){ parent[rooty] = rootx; }else{ parent[rootx] = rooty; } } } int find(int x) { if (parent[x] != x) { parent[x] = find(parent[x]); } return parent[x]; } private: vector<int> parent; }; class Solution { public: int largestComponentSize(vector<int>& nums) { int m = *max_element(nums.begin(), nums.end()); UnionFind uf(m + 1); //枚举每一个因数 for (int num : nums) { for (int i = 2; i * i <= num; i++) { if (num % i == 0) { uf.uni(num, i); uf.uni(num, num / i); } } } vector<int> counts(m + 1,0); int ans = 0; for (int num : nums) { int root = uf.find(num); counts[root]++; ans = max(ans, counts[root]); } return ans; } };
总结
在「并查集」数据结构中,其中心思想是将所有连接的顶点,无论是直接连接还是间接连接,都将他们指向同一个父节点或者根节点。此时,如果要判断两个顶点是否具有连通性,只要判断它们的根节点是否为同一个节点即可。
在「并查集」数据结构中,它的两个灵魂函数,分别是 find和 union。find 函数是为了找出给定顶点的根节点。 union 函数是通过更改顶点根节点的方式,将两个原本不相连接的顶点表示为两个连接的顶点。对于「并查集」来说,它还有一个重要的功能性函数 connected。它最主要的作用就是检查两个顶点的「连通性」。find 和 union 函数是「并查集」中必不可少的函数。connected 函数则需要根据题目的意思来决定是否需要。
并查集的代码是高度模板化的,建议熟记代码模板。