快速排序

快速排序比归并更常用，更高效的原因是——快排是原地排序，空间复杂度是O(logn)（这个是因为递归的深度，或者迭代时候的栈大小），但是归并排序的空间复杂度是O(n)（对于数组来说是这样的，因为要开辟额外的数组进行比较，但是对于链表则没有这个）。
同时，随机选取基准点的快排的平均时间复杂度一样是O(longn)，和归并排序并没什么区别。
步骤
- 1.选择基准；
- 2.根据基准排序，同时返回最后基准的位置；
- 3.更加返回的基准位置，递归基准位置的分半数组。注意递归的返回条件。
注意，数组要引用，才能原地覆盖。
快排的原则是先排序，后递归。
递归实现，空间复杂度是O(logn)。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50


#include <iostream>
#include <vector>
using namespace std;

int Partition(vector<int> &src, int left, int right) {
    // 使用快慢指针，左边小于，右边大于等于
    int pivot = src[left];
    int slowNode = left + 1;
    int fastNode = left + 1;
    while (fastNode <= right) {
        if (src[fastNode] < pivot) {
            swap(src[fastNode], src[slowNode]);
            ++slowNode;
        }
        ++fastNode;
    }
    // 交换基准位置
    swap(src[slowNode - 1], src[left]);
    // 返回基准位置
    return slowNode - 1;
}

// 快速排序，递归法，输入闭区间
void QuickSort(vector<int> &src, int left, int right) {
    // 结束条件，只剩一个元素
    if (right <= left) {
        return;
    }
    int pivot = Partition(src, left, right); // 返回基准
    // 递归
    QuickSort(src, left, pivot - 1);
    QuickSort(src, pivot + 1, right);
}

int main() {
    vector<int> test_num = {3, 8, 2, 3, 5, 1, 4, 7, 6};
    cout << "src num :" << endl;
    for (auto &i : test_num) {
        cout << i << " ";
    }
    cout << endl;
    int left = 0;
    int right = test_num.size() - 1;
    QuickSort(test_num, left, right);
    cout << "sort num :" << endl;
    for (auto &i : test_num) {
        cout << i << " ";
    }
    return 0;
}

非递归实现，空间复杂度是O(logn)。
方法——使用栈，栈的元素是开始和结束的位置。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60


#include <iostream>
#include <stack>
#include <vector>
using namespace std;

int Partition(vector<int> &src, int left, int right) {
    // 使用快慢指针,左边小于，右边大于等于
    int pivot = src[left];
    int slowNode = left + 1;
    int fastNode = left + 1;
    while (fastNode <= right) {
        if (src[fastNode] < pivot) {
            swap(src[fastNode], src[slowNode]);
            ++slowNode;
        }
        ++fastNode;
    }
    // 交换基准位置
    swap(src[slowNode - 1], src[left]);
    // 返回基准位置
    return slowNode - 1;
}

// 快速排序，非递归法,使用栈输入左右端点
void QuickSortV2(vector<int> &src, int left, int right) {
    stack<pair<int, int>> SaveStartEnd;
    SaveStartEnd.emplace(left, right);
    while (!SaveStartEnd.empty()) {
        pair<int, int> temp = SaveStartEnd.top();
        SaveStartEnd.pop();
        int LeftBoard = temp.first;
        int RightBoard = temp.second;
        // 退出条件
        if (RightBoard <= LeftBoard) {
            continue;
        }
        // 开始排序,同时返回基准位置
        int pivot = Partition(src, LeftBoard, RightBoard);
        // 插入堆栈
        SaveStartEnd.emplace(LeftBoard, pivot - 1);
        SaveStartEnd.emplace(pivot + 1, RightBoard);
    }
}

int main() {
    vector<int> test_num = {3, 8, 2, 5, 1, 3, 4, 7, 6};
    cout << "src num :" << endl;
    for (auto &i : test_num) {
        cout << i << " ";
    }
    cout << endl;
    int left = 0;
    int right = test_num.size() - 1;
    QuickSortV2(test_num, left, right);
    cout << "sort num :" << endl;
    for (auto &i : test_num) {
        cout << i << " ";
    }
    return 0;
}

快速选择

快速排序的变异，用于求取数组中第K个最大元素。
215. 数组中的第K个最大元素 - 力扣（LeetCode）

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49


class Solution {
  public:
    int ans;
    int Partition(vector<int> &src, int left, int right) {
        // 使用快慢指针
        int pivot = src[left];
        int slowNode = left + 1;
        int fastNode = left + 1;
        while (fastNode <= right) {
            if (src[fastNode] < pivot) {
                swap(src[fastNode], src[slowNode]);
                ++slowNode;
            }
            ++fastNode;
        }
        // 交换基准位置
        swap(src[slowNode - 1], src[left]);
        // 返回基准位置
        return slowNode - 1;
    }

    void quickselect(vector<int> &nums, int l, int r, int k) {
        if (ans != 0x3f3f3f3f) {
            return;
        }
        if (l >= r) {
            if (l == r && l == k) {
                ans = nums[k];
            }
            return;
        }
        int pivot = Partition(nums, l, r);
        if (pivot == k) {
            ans = nums[k];
            return;
        }
        if (k < pivot)
            quickselect(nums, l, pivot - 1, k);
        else
            quickselect(nums, pivot + 1, r, k);
    }

    int findKthLargest(vector<int> &nums, int k) {
        int n = nums.size();
        ans = 0x3f3f3f3f;
        quickselect(nums, 0, n - 1, n - k);
        return ans;
    }
};

归并排序

注意无论是递归还是迭代，空间复杂度都是O(n)，因为开辟了额外的数组。
思路：先递归，后排序，自底向上。
注意不要数组越界，一般记为mid 和 mid+1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69


/*
 * 合并，分别为[left,mid] [mid+1,right]
 */
void Merge(vector<int> &nums,int left,int mid,int right, vector<int> &tmp){
    for(int i = left;i<=right;++i){
        tmp[i]=nums[i];//先赋值一个数组
    }
    int k = left;
    int i = left;
    int j = mid+1;
    for(;k<=right;++k){
        if(i==mid+1){
            nums[k]=tmp[j];
            ++j;
        }else if(j==right+1){
            nums[k]=tmp[i];
            ++i;
        }
        //等于号保证是稳定排序
        else if(tmp[i]<=tmp[j]){
            nums[k]=tmp[i];
            ++i;
        }else{
            nums[k]=tmp[j];
            ++j;
        }
    }
}



//归并排序,先递归后合并
//最后的排序数组为nums，tmp是预先开辟的缓存数组
void MergeSort(vector<int> &nums,int left, int right, vector<int> &tmp){
    //递归结束条件
    if(left==right){
        return;
    }
    //mid始终小于right，所以mid+1合理的顺序
    int mid = left + (right-left)/2;
    //递归
    MergeSort(nums,left,mid,tmp);
    MergeSort(nums,mid+1,right,tmp);
    //一个优化点，如果已经排序好了，就不合并了
    if(nums[mid]<=nums[mid+1]){
        return;
    }
    //合并
    Merge(nums,left,mid,right,tmp);
}


int main(){
    cout<<"src nums : ";
    vector<int> sec={1,5,9,8,4,5,3,6,2,0,15,18};
    for(auto &i:sec){
        cout<<i<<", ";
    }
    cout<<endl;
    int n =sec.size();
    vector<int> temp(n);
    MergeSort(sec,0,n-1,temp);
    cout<<"sort nums : ";
    for(auto &i:sec){
        cout<<i<<", ";
    }
    cout<<endl;
    return 0;
}

非递归的归并排序算法，基础思路还是自底向上，并不需要使用栈，注意！

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49


#include <bits/stdc++.h>
using namespace std;

void Merge(vector<int> &nums, int left, int mid, int right, vector<int> &temp) {
    for (int i = left; i <= right; ++i) {
        temp[i] = nums[i];
    }
    int i = left, j = mid + 1;
    for (int k = left; k <= right; ++k) {
        if (i == mid + 1) {
            nums[k] = temp[j++];
        } else if (j == right + 1) {
            nums[k] = temp[i++];
        } else if (temp[i] <= temp[j]) {
            nums[k] = temp[i++];
        } else {
            nums[k] = temp[j++];
        }
    }
}

void MergeSort(vector<int> &nums) {
    int n = nums.size();
    vector<int> temp(n);
    // 自底向上的迭代方法，首先合并小的子数组，然后合并这些已经排序的子数组。每次迭代的步长sz都会翻倍，直到步长大于数组长度。
    for (int sz = 1; sz < n; sz *= 2) {
        for (int low = 0; low < n - sz; low += sz * 2) {
            int mid = low + sz - 1;
            int high = min(low + sz * 2 - 1, n - 1);
            Merge(nums, low, mid, high, temp);
        }
    }
}

int main() {
    cout << "src nums : ";
    vector<int> sec = {1, 5, 9, 8, 4, 5, 3, 6, 2, 0, 15, 18};
    for (auto &i : sec) {
        cout << i << ", ";
    }
    cout << endl;
    MergeSort(sec);
    cout << "sort nums : ";
    for (auto &i : sec) {
        cout << i << ", ";
    }
    cout << endl;
    return 0;
}

归并思想——逆序对的个数

剑指 Offer 51. 数组中的逆序对

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。
1 2

输入: [7,5,6,4] 输出: 5
思路：我们发现用这种「算贡献」的思想在合并的过程中计算逆序对的数量的时候，只在 rPtr 右移的时候计算，是基于这样的事实：rPtr右移表示左边的数都比rPtr大，即逆序了，所有就有mid+1-i个逆序对。把这种思路一直分解到最小的两个数判断，最后的总和就是逆序对个数。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66


class Solution {
public:
    int count_rev = 0;

    /*
    * 合并，分别为[left,mid] [mid+1,right]
    */
    void Merge(vector<int> &nums, int left, int mid, int right, vector<int> &tmp) {
        for (int i = left; i <= right; ++i) {
            tmp[i] = nums[i];//先赋值一个数组
        }
        int k = left;
        int i = left;
        int j = mid + 1;//右边
        for (; k <= right; ++k) {
            if (i == mid + 1) {
                nums[k] = tmp[j];
                ++j;
            } else if (j == right + 1) {
                nums[k] = tmp[i];
                ++i;
            }
                //等于号保证是稳定排序
            else if (tmp[i] <= tmp[j]) {
                nums[k] = tmp[i];
                ++i;
            } else {
                count_rev += mid + 1 - i;
                nums[k] = tmp[j];
                ++j;
            }
        }
    }


    //归并排序,先递归后合并
    //最后的排序数组为nums，tmp是预先开辟的缓存数组
    void MergeSort(vector<int> &nums, int left, int right, vector<int> &tmp) {
        //递归结束条件
        if (left == right) {
            return;
        }
        //mid始终小于right，所以mid+1合理的顺序
        int mid = left + (right - left) / 2;
        //递归
        MergeSort(nums, left, mid, tmp);
        MergeSort(nums, mid + 1, right, tmp);
        //一个优化点，如果已经排序好了，就不合并了
        if (nums[mid] <= nums[mid + 1]) {
            return;
        }
        //合并
        Merge(nums, left, mid, right, tmp);
    }

    int reversePairs(vector<int>& nums) {
        if(nums.empty()){
            return 0;
        }
        int n = nums.size();
        vector<int> temp(n);
        count_rev = 0;
        MergeSort(nums, 0, n - 1, temp);
        return count_rev;
    }
};

761. 特殊的二进制序列

特殊的二进制序列是具有以下两个性质的二进制序列：
- 0 的数量与 1 的数量相等。
- 二进制序列的每一个前缀码中 1 的数量要大于等于 0 的数量。
给定一个特殊的二进制序列 S，以字符串形式表示。定义一个操作为首先选择 S 的两个连续且非空的特殊的子串，然后将它们交换。（两个子串为连续的当且仅当第一个子串的最后一个字符恰好为第二个子串的第一个字符的前一个字符。)

在任意次数的操作之后，交换后的字符串按照字典序排列的最大的结果是什么？
思路：想象成左右括号对应问题，使用归并+排序。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40


class Solution {
public:
    string makeLargestSpecial(string s) {
        //归并+排序
        int n =s.size();
        if(n<=2){
            return s;
        }
        int cnt = 0;//记录左括号的次数
        int start = 0;//同一层次的括号的开始的地方
        vector<string> record;
        for(int i=0;i<n;++i){
            if(s[i] == '1'){
                ++cnt;
            }else{
                --cnt;
            }
            if(cnt==0){
                string curr;
                curr.push_back('1');
                //递归
                string tmp = makeLargestSpecial(s.substr(start+1,i-(start+1)));
                curr += tmp;
                curr.push_back('0');
                record.push_back(curr);
                //更新参数
                start = i+1;
            }
        }
        //同层次排序
        sort(record.begin(),record.end(),[](auto &i1, auto &i2){
            return i1>i2;
        });
        string ret;
        for(auto &i:record){
            ret+=i;
        }
        return ret;
    }
};

单链表的归并排序

对数组做归并排序需要的空间复杂度为O(n)-->新开辟数组O(n)+递归调用函数O(logn);
对链表做归并排序可以通过修改引用来更改节点位置，因此不需要向数组一样开辟额外的O(n)空间，但是只要是递归就需要消耗log(n)的空间复杂度，要达到O(1)空间复杂度的目标，得使用迭代法。
（1）递归法，此时的空间复杂度为 O(logn)。
- 自底向上归并
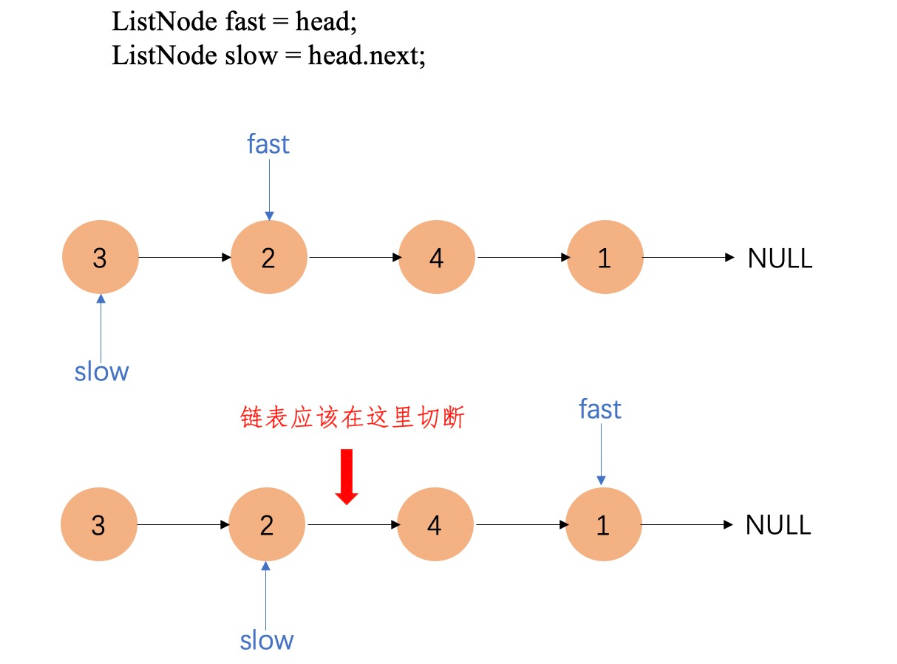
- 快慢指针找到一个链表的中间节点
- 合并两个已排好序的链表为一个新的有序链表

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53


struct ListNode {
    int val;
    ListNode *next;
    ListNode() : val(0), next(nullptr) {}
    ListNode(int x) : val(x), next(nullptr) {}
    ListNode(int x, ListNode *next) : val(x), next(next) {}
};

class Solution {
  public:
    ListNode *merge(ListNode *h1, ListNode *h2) {
        ListNode *dummp = new ListNode();
        ListNode *p = dummp;
        while (h1 && h2) {
            if (h1->val < h2->val) {
                p->next = h1;
                p = p->next;
                h1 = h1->next;
            } else {
                p->next = h2;
                p = p->next;
                h2 = h2->next;
            }
        }
        if (h1) {
            p->next = h1;
        } else if (h2) {
            p->next = h2;
        }
        return dummp->next;
    }

    ListNode *sortList(ListNode *head) {
        if (!head || !head->next) {
            return head;
        }
        // 找到中间节点并断开
        ListNode *slowNode = head;
        ListNode *fastNode = head->next;
        while (fastNode && fastNode->next) {
            slowNode = slowNode->next;
            fastNode = fastNode->next->next;
        }
        ListNode *rightHead = slowNode->next; // 链表第二部分的头节点
        slowNode->next = nullptr;

        // 递归排序
        ListNode *left = sortList(head);
        ListNode *right = sortList(rightHead);

        return merge(left, right);
    }
};

（2）迭代法：此时的空间复杂度为O（1），比较麻烦

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75


class Solution {
  public:
    ListNode *merge(ListNode *h1, ListNode *h2) {
        ListNode *dummp = new ListNode();
        ListNode *p = dummp;
        while (h1 && h2) {
            if (h1->val < h2->val) {
                p->next = h1;
                p = p->next;
                h1 = h1->next;
            } else {
                p->next = h2;
                p = p->next;
                h2 = h2->next;
            }
        }
        if (h1) {
            p->next = h1;
        } else if (h2) {
            p->next = h2;
        }
        return dummp->next;
    }

    // 求链表长度
    int getLength(ListNode *head) {
        // 获取链表长度
        int count = 0;
        while (head) {
            count++;
            head = head->next;
        }
        return count;
    }

    // 断链操作 返回第二部分链表头
    ListNode *split(ListNode *head, int step) {
        if (!head)
            return head;
        ListNode *cur = head;
        for (int i = 1; i < step && cur->next; i++) {
            cur = cur->next;
        }
        ListNode *right = cur->next;
        cur->next = nullptr; // 切断连接
        return right;
    }

    ListNode *sortList(ListNode *head) {
        int len = getLength(head);

        ListNode *dummp = new ListNode();
        dummp->next = head;
        ListNode *pre;
        ListNode *curr;
        ListNode *h1, *h2;
        for (int step = 1; step < len; step *= 2) {
            pre = dummp;
            curr = dummp->next;
            while (curr) {
                h1 = curr;
                h2 = split(h1, step);
                // 切换下一段
                curr = split(h2, step);
                ListNode *tmp = merge(h1, h2);
                pre->next = tmp;
                // 移动pre到已排序的末尾
                while (pre->next) {
                    pre = pre->next;
                }
            }
        }
        return dummp->next;
    }
};

堆排序

使用二叉堆为基础，建堆之后依次排出堆顶元素，进而形成有序序列。
实际写堆排序，可以使用优先队列进行排序，依次弹出优先队列的第一个元素即可完成排序。
时间复杂度分析：

排序算法笔记

快速排序

快速选择

归并排序

归并思想——逆序对的个数

单链表的归并排序

堆排序