数据结构概述

数组和链表是物理结构
顺序表、栈、队列、树、图是逻辑结构

数组

list内置类
list可以是任何对象
常见函数
增加元素

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


list.append(obj) #尾部增加元素
####例子
x = ['Monday', 'Tuesday', 'Wednesday', 'Thursday', 'Friday']
x.append('Thursday')
print(x)
# ['Monday', 'Tuesday', 'Wednesday', 'Thursday', 'Friday', 'Thursday']


list.insert(index, obj) #在编号 index 位置前插入 obj 
####例子
x = ['Monday', 'Tuesday', 'Wednesday', 'Thursday', 'Friday']
x.insert(2, 'Sunday')
print(x)
# ['Monday', 'Tuesday', 'Sunday', 'Wednesday', 'Thursday', 'Friday']



list.extend(seq)  #在列表末尾一次性追加另一个序列中的多个值（用新列表扩展原来的列表）

删除元素

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20


list.remove(obj)  #移除列表中某个值的第一个匹配项
####例子
x = ['Monday', 'Tuesday', 'Wednesday', 'Thursday', 'Friday']
x.remove('Monday')
print(x) # ['Tuesday', 'Wednesday', 'Thursday', 'Friday']



list.pop([index=-1])  #移除列表中的一个元素（默认最后一个元素），并且返回该元素的值
####例子
x = ['Monday', 'Tuesday', 'Wednesday', 'Thursday', 'Friday']
y = x.pop()
print(y) # Friday



del #已知位置，删除后不能返回使用
x = ['Monday', 'Tuesday', 'Wednesday', 'Thursday', 'Friday']
del x[0:2]
print(x) # ['Wednesday', 'Thursday', 'Friday']

查找、修改

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


# 直接使用索引值进行查找修改
week = ['Monday', 'Tuesday', 'Wednesday', 'Thursday', 'Friday']
print(len(week))
week[0]=1
week[2]=2
print(week)

'''
5
[1, 'Tuesday', 2, 'Thursday', 'Friday']
'''

链表

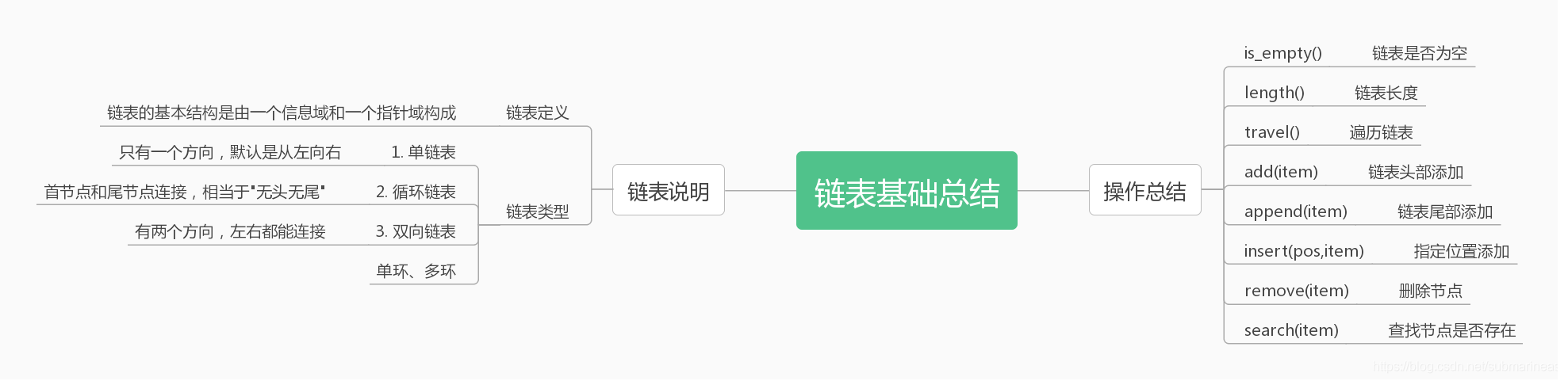
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96


# 单链表
class Node(object):
    def __init__(self, data):
        # 数据域
        self.data = data
        # 向后的引用域
        self.next = None


class SingleLinkList(object):
    def __init__(self):
        self.head = None

    # is_empty() 链表是否为空
    def is_empty(self):
        return not self.head

    # add(data) 链表头部添加元素
    # O(1)
    def add(self, data):
        node = Node(data)
        node.next = self.head
        self.head = node

    # show() 遍历整个链表
    # O(n)
    def show(self):
        cur = self.head
        while cur != None:
            # cur是一个有效的节点
            print(cur.data, end=' --> ')
            cur = cur.next
        print()

    # append(item) 链表尾部添加元素
    # O(n)
    def append(self, data):
        cur = self.head
        while cur.next != None:
            cur = cur.next
        # cur指向的就是尾部节点
        node = Node(data)
        cur.next = node

    # length() 链表长度
    # O(n)
    def length(self):
        count = 0
        cur = self.head
        while cur != None:
            # cur是一个有效的节点
            count += 1
            cur = cur.next
        return count

    # search(item) 查找节点是否存在
    # O(n)
    def search(self, data):
        cur = self.head
        while cur != None:
            if cur.data == data:
                return True
            cur = cur.next
        return False

    # remove(data) 删除节点
    # O(n)
    def remove(self, data):
        cur = self.head
        pre = None
        while cur != None:
            if cur.data == data:
                if cur == self.head:
                    self.head = self.head.next
                    return
                pre.next = cur.next
                return
            pre = cur
            cur = cur.next

    # insert(index, data) 指定位置添加元素
    # O(n)
    def insert(self, index, data):
        if index <= 0:
            self.add(data)
            return
        if index > self.length() - 1:
            self.append(data)
            return
        cur = self.head
        for i in range(index-1):
            cur = cur.next
        # cur指向的是第index节点第前置节点
        node = Node(data)
        node.next = cur.next
        cur.next = node

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122


# 双链表
class Node(object):
    #节点的类
    def __init__(self,item):
        self.item = item
        self.prev = None
        self.next = None

class DLinkList(object):
    #双向链表的类
    def __init__(self):
        #指向链表的头节点
        self.head = None

    def is_empty(self):
        #链表是否为空
        return self.head == None


    def length(self):
        #链表长度
        cur = self.head
        #计数器
        count = 0
        while cur != None:
            count += 1
            cur = cur.next
        return count

    def travel(self):
        #遍历链表
        cur = self.head
        while cur != None:
            print(cur.item)
            cur = cur.next

    def add(self,item):
        #链表头部添加
        node = Node(item)
        if self.is_empty():
            #如果是空链表，将head指向node
            #给链表添加第一个元素
            self.head = node
        else:
            #如果链表不为空，在新的节点和原来的首节点之间建立双向链接
            node.next = self.head
            self.head.prev = node
            #让head指向链表的新的首节点
            self.head = node


    def append(self,item):
        #链表尾部添加
        #创建新的节点
        node = Node(item)
        if self.is_empty():
            #空链表，
            self.head = node
        else:
            #链表不为空
            cur = self.head
            while cur.next != None:
                cur = cur.next
            #cur的下一个节点是node
            cur.next = node
            #node的上一个节点是
            node.prev = cur

    def insert(self,pos,item):
        #指定位置添加
        if pos <=0:
            self.add(item)
        elif pos > self.length()-1:
            self.append()
        else:
            node = Node(item)
            cur = self.head
            count = 0
            #把cur移动到指定位置的前一个位置
            while count < (pos - 1):
                count+=1
                cur = cur.next
            #node的prev指向cur
            node.prev = cur
            #node的next指向cur的next
            node.next = cur.next
            cur.next.prev = node
            cur.next = node

    def remove(self,item):
        #删除节点
        if self.is_empty():
            return
        else:
            cur = self._head
            if cur.item == item:
                #首节点是要删除的节点
                if cur.next == None:
                    #说明链表中只有一个节点
                    self.head = None
                else:
                    #链表多于一个节点的情况
                    cur.next.prev = None
                    self.head = cur.next
            else:
                # 首节点不是要删除的节点
                while cur != None:
                    if cur.item == item:
                        cur.prev.next = cur.next
                        cur.next.prev = cur.prev
                        break
                    cur = cur.next


    def search(self,item):
        #查找节点是否存在
        cur = self._head
        while cur != None:
            if cur.item == item:
                return True
            cur = cur.next
        return False

栈

直接使用list创建stack即可

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16


>>> stack=[]
>>> stack.append(1)
>>> stack.append(2)
>>> stack.append(3)
>>> stack
[1, 2, 3]
>>> stack.pop()   # 弹出栈顶元素
3
>>> stack.pop()
2
>>> stack
[1]
>>> stack.pop()
1
>>> stack
[]

队列

单向队列

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19


import queue
q = queue.Queue()
# 写
for i in range(5):
    q.put(i)
# 读
while not q.empty():
    print(q.get())
print(q.empty())


####
0
1
2
3
4
True
####

双向队列
- deque.append
- deque.appendleft
- deque.pop
- deque.popleft

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21


from collections import deque
queue=deque()
queue.append('a')
queue.append('b')
queue.append('c')
print(queue)
queue.appendleft('A')
queue.appendleft('B')
print(queue)
print(queue.pop())
print(queue.popleft())
print(queue)


####
deque(['a', 'b', 'c'])
deque(['B', 'A', 'a', 'b', 'c'])
c
B
deque(['A', 'a', 'b'])
####

哈希表——dict字典

数值、字符和元组都能被哈希，因此它们是不可变类型。
列表、集合、字典不能被哈希，因此它是可变类型。
用 hash(X) ，只要不报错，证明 X 可被哈希，即不可变，反过来不可被哈希，即可变。
字典以"关键字"为索引，关键字可以是任意不可变类型，通常用字符串或数值。
字典是无序的键:值（ key:value ）对集合，键必须是互不相同的（在同一个字典之内）。
1. dict 内部存放的顺序和 key 放入的顺序是没有关系的。
2. dict 查找和插入的速度极快，不会随着 key 的增加而增加，但是需要占用大量的内存。字典定义语法为 {元素1, 元素2, ..., 元素n}
3. 其中每一个元素是一个「键值对」-- 键:值 ( key:value )
4. 关键点是「大括号 {}」,「逗号 ,」和「冒号 :」
5. 大括号 -- 把所有元素绑在一起
6. 逗号 -- 将每个键值对分开
7. 冒号 -- 将键和值分开

1
2
3
4
5
6


dic = dict()
dic['a'] = 1
dic['b'] = 2
dic['c'] = 3
print(dic)
# {'a': 1, 'b': 2, 'c': 3}

二叉树的前序、中序、后序遍历（深度优先遍历）

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136


class TreeNode:
    def __init__(self,data):
        self.data=data
        self.left=None
        self.right=None


root= TreeNode(5)
root.left=TreeNode(7)
root.right=TreeNode(8)
root.left.left=TreeNode(3)
root.left.right=TreeNode(4)
root.right.left=TreeNode(6)

# 递归遍历
def pre_order_traversal(node):
    if node is None:
        return
    print(node.data)
    pre_order_traversal(node.left)
    pre_order_traversal(node.right)
    return node #返回根节点，不返回也没关系


def in_order_traversal(node):
    if node is None:
        return
    in_order_traversal(node.left)
    print(node.data)
    in_order_traversal(node.right)
    return node

def post_order_traversal(node):
    if node is None:
        return
    post_order_traversal(node.left)
    post_order_traversal(node.right)
    print(node.data)
    return node


# 非递归遍历
# 前序，使用栈数据结构，都具备回溯功能
def pre_order_traversal_with_stack(node):
    if node is None:
        return
    stack=[node]
    while len(stack)>0:
        node=stack.pop()
        # 前序，先打印
        print(node.data)
        # 栈的弹出顺序与入栈顺序相反 因此先入右再入左
        if node.right:
            stack.append(node.right)
        if node.left:
            stack.append(node.left)

# 中序遍历
def in_order_traversal_with_stack(node):
    if node is None:
        return
    stack=[]
    while node is not None or len(stack)>0:
        #节点不为空，疯狂压左节点入栈
        while node is not None:
            stack.append(node)
            node=node.left
        #左节点完成，输出一个值，看他的右节点，再疯狂压左节点
        if len(stack)>0:
            node=stack.pop()
            print(node.data)
            node=node.right


def post_order_traversal_with_stack(node):
    # 后序遍历二叉树非递归 后序遍历是 左-右-中
    # 反过来就是 中-右-左 其实就是前序遍历镜像二叉树(即左右互换)
    # 利用两个栈
    if node is None:
        return
    stack=[node]
    result=[]
    while len(stack)>0:
        node=stack.pop()
        # 结果入栈
        result.append(node.data)
        # 镜像前序二叉树，栈的弹出顺序与入栈顺序相反 因此先入左再入右
        if node.left:
            stack.append(node.left)
        if node.right:
            stack.append(node.right)
    while len(result)>0:
        print(result.pop())

        
        
def post_order_traversal_with_flag(node):
    # 后序遍历跟前序和中序不同的地方在于，访问完左子树后，会回溯到父节点，此时不能访问父节点，访问完右子树后，回溯到父节点，
    # 此时才能访问父节点。所以回溯到父节点的时候，要判断上一次操作访问的是哪里，
    # 如果上一次操作访问的时左子树，那么不可访问当前节点，得先去访问当前节点的右子树，
    # 如果上一次操作访问的是右子树，那么可以访问当前节点。
    if node is None:
        return
    stack=[]
    preVisited =None #访问标志
    while node is not None or len(stack)>0:
        #节点不为空，疯狂压左节点入栈
        while node is not None:
            stack.append(node)
            node=node.left
        if(len(stack)>0):
            node=stack[-1]# 读取最后一个节点，先不弹出
            # 右节点不存在或已经被访问过了
            if node.right is None or node.right==preVisited:
                print(node.data)
                stack.pop()
                preVisited=node
                node=None #防止重复访问，避免进入循环
            else:
                node=node.right



# pre_order_traversal(root)
# print('\n非递归')
# pre_order_traversal_with_stack(root)

# in_order_traversal(root)
# print('\n非递归')
# in_order_traversal_with_stack(root)

post_order_traversal(root)
print('\n')
post_order_traversal_with_stack(root)
print('\n')
post_order_traversal_with_flag(root)

二叉树的层序遍历（广度优先遍历）

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67


class TreeNode:
    def __init__(self,data):
        self.data=data
        self.left=None
        self.right=None

root= TreeNode(5)
root.left=TreeNode(7)
root.right=TreeNode(8)
root.left.left=TreeNode(3)
root.left.right=TreeNode(4)
root.right.left=TreeNode(6)
root.right.right=TreeNode(22)
root.left.right.left=TreeNode(33)

# 广度优先遍历——层序遍历
# 非递归思路：采用队列queue，出队一个根节点，入队两个子结点
from queue import Queue
def level_order_traversal(node):
    queue=Queue()
    queue.put(node)
    while not queue.empty():
        node=queue.get()
        print(node.data)
        if node.left is not None:
            queue.put(node.left)
        if node.right is not None:
            queue.put(node.right)


# 递归思路：依次打印出每一层，输入根节点和高度（从1开始）
def level_order_traversal_recurrence(node,level):
    if node is None or level==0:
        return
    if level==1:
        print(node.data)
    level_order_traversal_recurrence(node.left,level-1)
    level_order_traversal_recurrence(node.right,level-1)
# 高度为4
for i in range(1,5):
    level_order_traversal_recurrence(root,i)

print('\n非递归')
level_order_traversal(root)

'''
#####结果
5
7
8
3
4
6
22
33

非递归
5
7
8
3
4
6
22
33
#####
'''

二叉堆

二叉堆是一个完全二叉树，储存方式为顺序存储，即存储在数组里，python里面即列表list
如何定位左右孩子，依靠数组下标实现，从0开始，左孩子下标为2*parent+1，右孩子为2*parent+2。
最大堆：任何一个父节点的值，都大于或等于左孩子和右孩子的节点的值，堆顶为最大值
最小堆：任何一个父节点的值，都小于或等于左孩子和右孩子的节点的值，堆顶为最小值
三种操作：
- 尾结点插入——上浮
- 堆顶删除——下沉
- 二叉堆的构建（依次从最大非叶子节点下沉）

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81


# 以最小堆为例

# 二叉堆的插入，尾结点上浮操作，以最小堆为例
def up_adjust(array=[]):
    child_index = len(array) - 1  # 下标从0开始
    parent_index = (child_index - 1) // 2  # 除以2，向下取整
    temp = array[child_index]
    while child_index > 0 and temp < array[parent_index]:
        # temp一直存在比较，只需要单向赋值
        array[child_index] = array[parent_index]
        child_index = parent_index
        parent_index = (child_index - 1) // 2  # 除以2，向下取整
    array[child_index] = temp


# 二叉堆的删除，堆顶下沉操作，删除堆顶，尾结点放在堆顶上，以最小堆为例
def down_adjust(array=[]):
    tem = array.pop()
    array[0] = tem
    length = len(array)
    parent_index = 0
    child_index = 2 * parent_index + 1  # 左孩子下标
    while child_index < length:
        # 存在右孩子且比左孩子小
        if child_index + 1 < length and array[child_index + 1] < array[child_index]:
            child_index += 1
        # 父节点的值最小，直接返回
        if tem <= array[child_index]:
            break
        # 直接单向赋值
        array[parent_index] = array[child_index]
        parent_index = child_index
        child_index = 2 * parent_index + 1
    array[parent_index] = tem


# 二叉堆的下沉函数，用于创建二叉堆的迭代过程，最小堆为例
def down_for_build(parent_index, array=[]):
    tem = array[parent_index]
    child_index = parent_index * 2 + 1
    length = len(array)
    while child_index < length:
        # 存在右孩子且比左孩子小
        if child_index + 1 < length and array[child_index + 1] < array[child_index]:
            child_index += 1
        # 父节点的值最小，直接返回
        if tem <= array[child_index]:
            break
        # 直接单向赋值
        array[parent_index] = array[child_index]
        parent_index = child_index
        child_index = 2 * parent_index + 1
    array[parent_index] = tem


# 二叉堆的创建过程，最小堆的为例：
def build_heap(array=[]):
    # 列表下标为0开始，所以要多减一个1，即减2，从最后一个非叶子节点开始
    for i in range((len(array) - 2) // 2, -1, -1):
        down_for_build(i, array)

myarray = list([1, 3, 2, 6, 5, 7, 8, 9, 10,0])
up_adjust(myarray)
print(myarray)

myarray1 = list([1, 3, 2, 6, 5, 7, 8, 9, 10])
down_adjust(myarray1)
print(myarray1)

myarray2=list([7,1,3,10,5,2,8,9,6])
build_heap(myarray2)
print(myarray2)


####输出
'''
[0, 1, 2, 6, 3, 7, 8, 9, 10, 5]
[2, 3, 7, 6, 5, 10, 8, 9]
[1, 5, 2, 6, 7, 3, 8, 9, 10]

'''

优先队列

二叉堆的变形
最大优先队列：无论入队顺序如何，当前最大元素都会优先出队，基于最大堆实现的
最小优先队列：无论入队顺序如何，当前最小元素都会优先出队，基于最小堆实现的
入队：即二叉堆的尾结点上浮
出队：即二叉堆的堆顶删除，尾结点替代堆顶，然后下沉操作

排序算法

主流十大排序，分成三类
- 时间复杂度为O(N^2^)的排序算法：
  - 冒泡排序——稳定
  - 选择排序——不稳定
  - 插入排序——稳定
  - 希尔排序（性能略优于O(N^2^)，但比不上O(nlogn)）——不稳定
- 时间复杂度为O(nlogn)）的排序算法：
  - 快速排序——不稳定
  - 归并排序——稳定
  - 堆排序——不稳定
- 时间复杂度为线性的排序算法：（均为非比较排序）
  - 计数排序——稳定
  - 桶排序——稳定
  - 基数排序——稳定
稳定排序和不稳定排序：值相同的元素排序前后位置是否改变判定

冒泡排序

最简单的冒泡排序：思路，两层for循环

1
2
3
4
5
6
7
8
9


# 冒泡算法
def bubble_sort_v1(array=[]):
    # 注意减1，避免溢出读取位置
    for i in range(len(array) - 1):
        for j in range(len(array) - i - 1):
            if array[j] > array[j + 1]:
                tem = array[j]
                array[j] = array[j + 1]
                array[j + 1] = tem

冒泡算法优化1：
- 思路：利用标记判断是否已经有序，是的话退出循环

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


# 冒泡算法优化1：判断数列已经有序，直接退出，利用标记
def bubble_sort_v2(array=[]):
    for i in range(len(array) - 1):
        # 是否有序的标记，初始化为true
        is_sorted = True
        for j in range(len(array) - i - 1):
            if array[j] > array[j + 1]:
                tem = array[j]
                array[j] = array[j + 1]
                array[j + 1] = tem
                # 有元素交换，并非有序
                is_sorted = False
        if is_sorted:
            # 仍为真，说明已经有序，提前退出
            break

冒泡算法优化2：设立有序边界
- 思路：每次交换后的index保存，在下一次大循环的时候重新设立截止边界

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21


# 冒泡排序优化2：有序边界可能不止是1、2、3...，实际可能比更多，每一步更新有序边界即为优化的点
def bubble_sort_v3(array=[]):
    # 更新的边界
    last_exchange_index = len(array) - 1
    # 初始化有序边界
    sort_border = last_exchange_index
    for i in range(len(array) - 1):
        # 是否有序的标记，初始化为true
        is_sorted = True
        for j in range(sort_border):
            if array[j] > array[j + 1]:
                tem = array[j]
                array[j] = array[j + 1]
                array[j + 1] = tem
                # 更新有序标记
                is_sorted = False
                # 更新有序边界
                last_exchange_index = j
        if is_sorted:
            break
        sort_border = last_exchange_index

鸡尾酒排序
- 冒泡排序的进阶
- 思路：左右进行排序，初始设置的有序边界都是i（即递增的0,1,2...）
- 适用于内部很多已经排好序的数组

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31


# 鸡尾酒排序，冒泡排序的进阶，适用大部分已经排好序的数组
def cock_tail_sort(array=[]):
    # 注意向下取整
    for i in range(len(array) // 2):
        # 奇数轮，从左往右
        # 是否有序的标记，初始化为true
        is_sorted = True
        for j in range(i, len(array) - i - 1):
            if array[j] > array[j + 1]:
                tem = array[j]
                array[j] = array[j + 1]
                array[j + 1] = tem
                # 有元素交换，并非有序
                is_sorted = False
        if is_sorted:
            # 仍为真，说明已经有序，提前退出
            break

        # 偶数轮，从右往左
        is_sorted = True
        # 最后一个已经排好序了，多减1变为减2
        for j in range(len(array) - i - 2, i, -1):
            if array[j] < array[j - 1]:
                tem = array[j]
                array[j] = array[j - 1]
                array[j - 1] = tem
                # 有元素交换，并非有序
                is_sorted = False
        if is_sorted:
            # 仍为真，说明已经有序，提前退出
            break

鸡尾酒排序的进阶：增加有序边界

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54


# 鸡尾酒排序优化，加入有序边界
def cock_tail_sort_v2(array=[]):
    # 奇数轮有序边界
    last_exchange_index_left = len(array) - 1
    # 初始化奇数轮有序边界
    sort_border_left = last_exchange_index_left
    # 偶数轮有序边界
    last_exchange_index_right = 0
    # 初始化奇数轮有序边界
    sort_border_right = last_exchange_index_right
    # 注意向下取整
    for i in range(len(array) // 2):
        # 奇数轮，从左往右
        # 是否有序的标记，初始化为true
        is_sorted = True
        for j in range(i, sort_border_left):
            if array[j] > array[j + 1]:
                tem = array[j]
                array[j] = array[j + 1]
                array[j + 1] = tem
                # 有元素交换，并非有序
                is_sorted = False
                # 更新有序边界
                last_exchange_index_left = j
        if is_sorted:
            # 仍为真，说明已经有序，提前退出
            break
        sort_border_left = last_exchange_index_left

        # 偶数轮，从右往左
        is_sorted = True
        # 最后一个已经排好序了，多减1变为减2
        for j in range(len(array) - i - 2, sort_border_right, -1):
            if array[j] < array[j - 1]:
                tem = array[j]
                array[j] = array[j - 1]
                array[j - 1] = tem
                # 有元素交换，并非有序
                is_sorted = False
                # 更新有序边界
                last_exchange_index_right = j
        if is_sorted:
            # 仍为真，说明已经有序，提前退出
            break
        sort_border_right = last_exchange_index_right


myarray2 = list([8, 2, 3, 4, 5, 6, 7, 15, 1])
cock_tail_sort_v2(myarray2)
print(myarray2)

'''
[1, 2, 3, 4, 5, 6, 7, 8, 15]
'''

选择排序

算法思想：
- A.在未排序序列中找到最小（大）元素，存放到排序序列的起始位置
- B.从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾
- C.以此类推，直到所有元素均排序完毕
与冒泡排序不同的是，选择排序是先找到最小值，然后交换位置。冒泡排序是每一次都交换，最后一定是最小值。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20


# 选择排序，按最大排序
def select_sort(array=[]):
    for i in range(0,len(array) - 1):
        flag = i
        for j in range(i+1, len(array) , 1):
            if (array[j] > array[flag]):
                flag = j
        tem = array[i]
        array[i] = array[flag]
        array[flag] = tem


myarray1 = list([-1.2, 4.6, 3.5, 4.4, 5.5, 6.8, 7.9, 15.2, 1.1, 16.4])
select_sort(myarray1)
print(myarray1)


'''
[16.4, 15.2, 7.9, 6.8, 5.5, 4.6, 4.4, 3.5, 1.1, -1.2]
'''

插入排序

它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。插入排序在实现上，通常采用in-place排序（即只需用到O(1)的额外空间的排序），因而在从后向前扫描过程中，需要反复把已排序元素逐步向后挪位，为最新元素提供插入空间。
和冒泡排序的区别在于，冒泡排序是拿一个元素和无序序列去遍历比较，比较得到整个无序序列中最值，然后放入有序序列，而一旦放入有序序列，就不再碰了。
插入排序是拿一个元素和有序的数列去比，从单一元素的假有序一个一个加，拿一个元素进入有序序列，碰到比自己大或小的就即刻坐下，不再继续比较，插入排序的当前元素是无论如何不会触摸无序序列的。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54


# 插入排序
def insertion_sort(array=[]):
    for i in range(1,len(array),1):
        # 是否进入有序序列
        if(array[i]<array[i-1]):
            tem=array[i]
            flag=i-1
            for j in range(i-1,-1,-1):
                # 开辟空间
                if array[j]>tem:
                    array[j + 1] = array[j]
                    flag=j
            array[flag]=tem


myarray1 = list([-1.2, 4.6, 3.5, 4.4, 5.5, 6.8, 7.9, 15.2, 1.1, 16.4])
insertion_sort(myarray1)
print(myarray1)

'''
[-1.2, 1.1, 3.5, 4.4, 4.6, 5.5, 6.8, 7.9, 15.2, 16.4]
'''


# 或者使用while循环
# 插入排序
def insertion_sort(array=[]):
    for i in range(1, len(array), 1):
        # 是否进入有序序列
        if (array[i] < array[i - 1]):
            tem = array[i]
            flag = i - 1
            while flag >= 0 and array[flag] > tem:
                array[flag + 1] = array[flag]
                flag -= 1
            array[flag+1] = tem


myarray1 = list([-1.2, 4.6, 3.5, 4.4, 5.5, 6.8, 7.9, 15.2, 1.1, 16.4])
insertion_sort(myarray1)
print(myarray1)


# 以下更简洁，同时衔接希尔排序
# 插入排序
def insertion_sort(array=[]):
    #gap=1
    for i in range(1, len(array), 1):
        tem = array[i]
        flag = i
        while flag >= 1 and array[flag-1] > tem:
            array[flag] = array[flag-1]
            flag -= 1
        array[flag] = tem

希尔排序

希尔排序(Shell's Sort)是插入排序的一种又称“缩小增量排序”（Diminishing Increment Sort），是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。
分组依次插入排序，设置依次整除2

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22


# 希尔排序
def shell_sort(array=[]):
    length=len(array)
    # 选择增量
    gap=length//2
    while gap:
        # gap即第二个元素，所以是分组插入排序
        for i in range(gap,length,1):
            tem=array[i]
            j=i
            while j>=gap and tem<array[j-gap]:
                array[j]=array[j-gap]
                #以下是分组的间隔
                j-=gap
            array[j]=tem
        gap=gap//2



myarray1 = list([-1.2, 4.6, 3.5, 4.4, 5.5, 6.8, 7.9, 15.2, 1.1, 16.4])
shell_sort(myarray1)
print(myarray1)

快速排序

思路：分治法
基准元素的选择：一般选择第一个元素，也可以随机选取之后和第一个元素调换，避免极端情况
双边循环递归法查找分界索引位置
- 使用双指针

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35


# 快速排序
# 思路：分治法，双边循环递归
def quick_sort(start_index,end_index,array=[]):
    # 递归结束条件：start_index>=end_index
    if start_index>=end_index:
        return
    #获取基准元素
    pivot_index=partition_v1(start_index,end_index,array)
    # 根据基准元素，分成两部分进行递归
    quick_sort(start_index,pivot_index-1,array)
    quick_sort(pivot_index+1,end_index,array)

def partition_v1(start_index,end_index,array=[]):
    #取第一个元素为基准元素
    pivot=array[start_index]
    #循环指针
    left=start_index
    right=end_index
    while left!=right:
        #控制right指针左移，大于等于基准元素才左移，此时是正确的顺序
        while left<right and array[right]>=pivot:
            right-=1
        # 控制left指针右移，小于等于基准元素才左移，此时是正确的顺序
        while left<right and array[left]<=pivot:
            left+=1
        # 交换元素
        if left<right:
            tem=array[left]
            array[left]=array[right]
            array[right]=tem

    # 指针重合,返回分区位置
    array[start_index]=array[left]
    array[left]=pivot
    return left

单边循环递归法
- 使用mark标志，左边比基准元素小，右边比基准元素大

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28


# 快速排序
# 思路：分治法，单边循环递归
def quick_sort_v2(start_index, end_index, array=[]):
    # 递归结束条件：start_index>=end_index
    if start_index >= end_index:
        return
    # 获取基准元素
    pivot_index = partition_v2(start_index, end_index, array)
    # 根据基准元素，分成两部分进行递归
    quick_sort(start_index, pivot_index - 1, array)
    quick_sort(pivot_index + 1, end_index, array)


def partition_v2(start_index, end_index, array):
    # 确定基准元素
    pivot = array[start_index]
    mark = start_index
    # 所有都要遍历，所以end_index+1
    for i in range(start_index + 1, end_index + 1):
        if array[i] < pivot:
            mark += 1
            if i != mark:
                tem = array[mark]
                array[mark] = array[i]
                array[i] = tem
    array[start_index] = array[mark]
    array[mark] = pivot
    return mark

非递归方法
- 使用栈
- 输入的是哈希表，包含读取的头和尾

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35


# 快速排序
# 思路：分治法，非递归，使用栈，栈中元素为哈希
def quick_sort_v3(start_index, end_index, array=[]):
    stack = []
    root_param = {"start_index": start_index, "end_index": end_index}
    stack.append(root_param)
    # 循环结束条件，栈为空
    while len(stack) > 0:
        # 栈顶元素出栈，得到开始停止的下标
        param = stack.pop()
        pivot = partition_v3(param.get("start_index"), param.get("end_index"), array)
        # 根据返回基准位置，划分左右哈希入栈
        if param.get("start_index") < (pivot - 1):
            left_param = {"start_index": start_index, "end_index": pivot - 1}
            stack.append(left_param)
        if param.get("end_index") > (pivot + 1):
            right_param = {"start_index": pivot + 1, "end_index": end_index}
            stack.append(right_param)


def partition_v3(start_index, end_index, array):
    # 确定基准元素
    pivot = array[start_index]
    mark = start_index
    # 所有都要遍历，所以end_index+1
    for i in range(start_index + 1, end_index + 1):
        if array[i] < pivot:
            mark += 1
            if i != mark:
                tem = array[mark]
                array[mark] = array[i]
                array[i] = tem
    array[start_index] = array[mark]
    array[mark] = pivot
    return mark

归并排序

思路：分治法
先分解，后归并
采用递归方式

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42


def merge_sort(array=[]):
    sort(0, len(array) - 1, array)

def sort(L, R, array=[]):
    if L == R:
        return
    mid = L + (R - L) // 2
    # 分解
    sort(L, mid, array)
    sort(mid + 1, R, array)
    # 归并
    merge(L, mid, R, array)


def merge(L, mid, R, array=[]):
    tem = [0] * (R - L + 1)
    # 比较两部分元素，填入缓存数组，或者用三端while也可以，不用for + if
    p_left = L
    p_right = mid + 1
    for i in range(0, (R - L + 1), 1):
        if p_left <= mid and p_right <= R:
            if array[p_left] < array[p_right]:
                tem[i] = array[p_left]
                p_left += 1
            else:
                tem[i] = array[p_right]
                p_right += 1
        elif p_left<=mid:
            tem[i] = array[p_left]
            p_left += 1
        elif p_right<=R:
            tem[i] = array[p_right]
            p_right += 1

    # 返回原数组
    for i in range(len(tem)):
        array[L + i] = tem[i]


myarray1 = list([-1.2, 4.6, 3.5, 4.4, 5.5, 6.8, 7.9, 15.2, 1.1, 16.4])
merge_sort(myarray1)
print(myarray1)

堆排序

无序数组构建二叉堆
- 从小到大排序，用最大堆
- 从大到小排序，用最小堆
循环删除堆顶元素，替换到二叉堆的末尾，堆顶下沉产生新的堆顶。
注意点，二叉堆的创建函数，输入参数要多加一个长度，避免array[:i]创建了新的数组输入，没有在原数组上更改

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33


# 堆排序
# 二叉堆的下沉函数，用于创建二叉堆的迭代过程，最小堆为例
def down_for_build(parent_index, length, array=[]):
    tem = array[parent_index]
    child_index = parent_index * 2 + 1
    # length = len(array)
    while child_index < length:
        # 存在右孩子且比左孩子小
        if child_index + 1 < length and array[child_index + 1] < array[child_index]:
            child_index += 1
        # 父节点的值最小，直接返回
        if tem <= array[child_index]:
            break
        # 直接单向赋值
        array[parent_index] = array[child_index]
        parent_index = child_index
        child_index = 2 * parent_index + 1
    array[parent_index] = tem


def heap_sort(array=[]):
    # 创建最小二叉堆
    # 列表下标为0开始，所以要多减一个1，即减2，从最后一个非叶子节点开始，因为2*x+1等于左孩子
    for i in range((len(array) - 2) // 2, -1, -1):
        down_for_build(i, len(array), array)

    # 循环交换尾部元素到堆顶，并调节堆产生新的堆顶
    for i in range(len(array) - 1, 0, -1):
        tem1 = array[i]
        array[i] = array[0]
        array[0] = tem1
        # 调节最小堆
        down_for_build(0, i, array)

计数排序

是一种非比较排序，是按数组下标来进行排序
步骤：（以下是优化版本，得出的排序是一种稳定排序）
- 求数组最大最小值，得出数组长度max-min+1
- 创建统计数组，统计对应元素个数，注意min作为偏移量
- 统计数组变形，后面元素等于前面元素之和
- 倒序遍历原始数组，从统计数组找到正确位置，输出排序数组

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35


# 计数排序
def count_sort(array=[]):
    # 1.得出最大最小值
    max_value = max(array)
    print(max_value)
    min_value = min(array)
    print(min_value)
    d = max_value - min_value + 1
    # 2.创建统计数组并统计对应元素个数,注意偏移量
    count_array = [0] * d
    for i in range(0, len(array)):
        count_array[array[i] - min_value] += 1
    # 3.统计数组变形，后面元素等于前面元素之和
    for i in range(1, len(count_array)):
        count_array[i] += count_array[i - 1]
    # 4.倒序遍历原始数组，从统计数组找到正确位置，输出排序数组
    sort_array = [0] * len(array)
    for i in range(len(array) - 1, -1, -1):
        # 减1是因为数组从0开始
        sort_array[count_array[array[i] - min_value] - 1] = array[i]
        # 位置减1，保证排序稳定性
        count_array[array[i] - min_value] -= 1
    return sort_array


myarray1 = list([8, 2, 3, 4, 5, 6, 7, 15, 1, 16])
myarray2=count_sort(myarray1)
print(myarray2)


'''
16
1
[1, 2, 3, 4, 5, 6, 7, 8, 15, 16]
'''

桶排序

可以进行小数的排序，克服计数排序只能进行整数排序的缺点
重点在于标号的计算，向下取整得出桶的序号
我们这种分法：
- 桶的数量等于原数组元素的数量
- 最后一个桶只有最大值
- 区间跨度=（max-min）/（桶的数量-1）
- 例如
  - [0.5,1.5), [1.5,2.5), [2.5,3.5), [3.5,4.5), [4.5,4.5]

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37


# 桶排序
def bucket_sort(array=[]):
    # 1.计算最大最小值，得出差值d
    max_value = max(array)
    min_value = min(array)
    d = max_value - min_value
    # 2.初始化桶，列表的列表
    bucket_num = len(array)
    bucket_list = []
    for i in range(0, bucket_num):
        bucket_list.append([])  # 子集为列表
    # 3.遍历原始数组，将每个元素放入桶中，利用向下取整，math.floor或者int()都行
    for i in range(0, len(array)):
        num = int((array[i] - min_value) * (bucket_num - 1) / d)
        bucket = bucket_list[num]
        bucket.append(array[i])
    # 4.对每个桶进行内部排序，此处调用python内部的sort函数，归并排序原理，注意归并排序并不稳定，最好用冒泡之类的进行稳定排序，保证桶排序的稳定性
    for i in range(len(bucket_list)):
        bucket_list[i].sort()
    # 5.输出全部元素
    sort_array = []
    for sub_list in bucket_list:
        for element in sub_list:
            sort_array.append(element)
    return sort_array


myarray1 = list([-1.2, 4.6, 3.5, 4.4, 5.5, 6.8, 7.9, 15.2, 1.1, 16.4])
myarray2 = bucket_sort(myarray1)
print(myarray2)



'''
[-1.2, 1.1, 3.5, 4.4, 4.6, 5.5, 6.8, 7.9, 15.2, 16.4]

'''

基数排序

思路：整数按位数切割成不同的数字，然后按每个位数分别比较。基数排序的方式可以采用LSD（Least significant digital）或MSD（Most significant digital），LSD的排序方式由键值的最右边开始，而MSD则相反，由键值的最左边开始。
MSD：先从高位开始进行排序，在每个关键字上，可采用计数排序（计数排序其实也是桶排序）
LSD：先从低位开始进行排序，在每个关键字上，可采用桶排序
注意，内部排序的方式一定是稳定排序，不然结果会出错，所以用计数排序和桶排序
MSD的方式由高位数为基底开始进行分配，但在分配之后并不马上合并回一个数组中，而是在每个“桶子”中建立“子桶”，将每个桶子中的数值按照下一数位的值分配到“子桶”中。在进行完最低位数的分配后再合并回单一的数组中。
LSD：不需要子桶排序

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24


def radix_sort(array=[]):
    """基数排序"""
    i = 0  # 记录当前正在排拿一位，最低位为1
    max_num = max(array)  # 最大值
    j = len(str(max_num))  # 记录最大值的位数
    bucket_list = []

    while i < j:
        bucket_list = [[] for _ in range(10)]  # 初始化桶数组,重新初始化10个列表集合
        # bucket_list.clear()
        # for num in range(0, 10):
        #     bucket_list.append([])  # 初始化桶列表
        for x in array:
            bucket_list[int(x / (10 ** i)) % 10].append(x)  # 找到位置放入桶数组
        array.clear()
        for x in bucket_list:  # 直接放回原序列
            for y in x:
                array.append(y)
        i += 1


myarray1 = list([334, 5, 67, 345, 7, 345345, 99, 4, 23, 78, 45, 1, 3453, 23424])
radix_sort(myarray1)
print(myarray1)

MSD：最高位优先法通常是一个递归的过程：

<1>先根据最高位关键码K1排序，得到若干对象组，对象组中每个对象都有相同关键码K1。

<2>再分别对每组中对象根据关键码K2进行排序，按K2值的不同，再分成若干个更小的子组，每个子组中的对象具有相同的K1和K2值。

<3>依此重复，直到对关键码Kd完成排序为止。

<4>最后，把所有子组中的对象依次连接起来，就得到一个有序的对象序列。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26


'''
    max_num = max(array)  # 最大值
    j = len(str(max_num))  # 记录最大值的位数
    d = j-1
'''

def radix_sort_msd(d, array=[]):
    length = len(array)
    bucket_list = [[] for _ in range(10)]  # 初始化桶数组,重新初始化10个列表集合
    if d >= 0 and length > 1:
        for x in array:
            bucket_list[int(x / (10 ** d)) % 10].append(x)  # 找到位置放入桶数组
    else:
        return
    # 进行子桶排序
    for i in range(10):
        radix_sort_msd(d - 1, bucket_list[i])
    array.clear()
    for x in bucket_list:  # 子桶更改原序列
        for y in x:
            array.append(y)


myarray1 = list([334, 5, 67, 345, 7,27, 345345, 99, 4, 23, 78, 45,46, 1, 3453, 23424])
radix_sort_msd(4, myarray1)
print(myarray1)

Python数据结构学习笔记