经验之谈

• 简化long long 类型

  • 1 2 3

    typedef long long ll; //或者 using ll = long long;

• 对于a--和--a的区别。其中a-- 表示先用后减；--a表示先减后用。

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

  #include <bits/stdc++.h> using namespace std; using ll = long long ; int main() { int idx = 5; while(--idx){ cout<<idx<<endl; } return 0; } /*输出结果:只有四次循环，1到n-1 4 3 2 1 */

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

  #include <bits/stdc++.h> using namespace std; using ll = long long ; int main() { int idx = 5; while(idx--){ cout<<idx<<endl; } return 0; } /*输出结果：循环五次，0到n-1 4 3 2 1 0 */

• 5大常用的算法：动态规划、回溯、分治法、贪心法则、分支限界算法。

  • 回溯算法是深度优先，那么分支限界法就是广度优先的一个经典的例子。回溯法一般来说是遍历整个解空间，获取问题的所有解，而分支限界法则是获取一个解（一般来说要获取最优解）。
  • 参考

• vector输入最好使用[]下标读写，使用迭代器iterator比较复杂且耗时。

• c++中单引号和双引号的区别

  • 单引号是字符型变量值，代表 ASCII 码中的一个值，根据不同的输出方式可以为整数或是字母。

  • 双引号是字符串型变量值，代表一个字符串。给字符串赋值时，系统会自动给字符串变量后边加上一个 “\0” 表示字符串结尾。而变量名字代表的是该字符串的起始指针。

  • 1 2 3 4 5 6 7

    '0' // char "0" // string "0\0" /*因此，使用'5'-'0'得到正确的序列5 使用"5"-"0"得到错误的序列 类似的还有'b'-'a'=1

• C++中常量INT_MAX和INT_MIN分别表示最大、最小整数，定义在头文件limits.h

• 牛客网代码信息：

  编译器信息

  版本：clang++3.9，采用c++11标准，编译的时候采用-O2级优化，支持万能头文件 <bits/stdc++.h>。

  输入输出处理

  1. 核心代码模式处理

  不需要处理任何输入输出，直接返回值即可。

  2. ACM 模式

  你的代码需要处理输入输出，请使用如下样例代码读取输入和打印输出：

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34

  //例一 #include <iostream> #include <algorithm> #include<string> #include<vector> using namespace std; int main() { int a, b; while (cin >> a >> b) { // 注意 while 处理多个 case cout << a + b << endl; } } // 64 位输出请用 printf("%lld") //例二 #include<iostream> #include<vector> using namespace std; int main() { int n; while (cin >> n) { vector<int> gym(n); vector<int> work(n); for (int i = 0; i < n; i++) cin >> work[i]; for (int i = 0; i < n; i++) cin >> gym[i]; int result = 0; // 处理逻辑 cout << result << endl; } return 0; }

• 万能头文件

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27

  #include <iostream> #include <cstdio> #include <fstream> #include <algorithm> #include <cmath> #include <deque> #include <vector> #include <queue> #include <string> #include <cstring> #include <map> #include <stack> #include <set> using namespace std; int main(){ return 0; } //----------------------------------------------- #include<bits/stdc++.h> using namespace std; int main(){ return 0; }

常见笔试函数

• 最小公约数

  • 思路：辗转相除法

  • 1 2 3 4 5 6 7

    int gcd(int x, int y) { if (x % y == 0) return y; else return gcd(y, x % y); }

• 判断大小写字母及数字

  1 2 3 4 5 6

  auto ii = islower('5');//判断小写 auto jj = isdigit('K');//判断数字 auto dd = isupper('a');//判断大小 isalpha(char c);//判断是否是字母 c = toupper(char c);//转换为大写字母 d = tolower(d);//转换为小写字母

• c++ 整数转为字符串

  • to_string(int value)；函数

• c++字符串转为整数

  • atoi(string s)

  • 1 2	string s = "15"; int n =atoi(s.c_str());

  • 也可以使用stoi 函数

  • 1 2	string a = "1999"; int ad = stoi(a);

• c++按空格或者逗号分隔字符串，除了遍历分隔外，还可以利用stringsteam字符串流就行处理

  • 按空格分隔

  • 1 2 3 4 5 6

    string s1("1 2 3"); stringstream ss(s1); string s2(""); while(getline(ss, s2, ' ')) { cout << s2 << endl; }

  • 按逗号分隔

  • 1 2 3 4 5 6

    string s1("1,2,3"); stringstream ss(s1); string s2(""); while(getline(ss, s2, ',')) { cout << s2 << endl; }

• memset函数是按照字节对内存块进行初始化，所以不能用它将int数组出初始化为0和-1之外的其他值

  • memset(a,0,sizeof(a))

• 利用位运算快速转换为大小写字母

  • 因为大小写相差为32，利用异或运算a=a^32。

  • 无论是小写转大写，还是大写转小写，都可以。

vector 数组

• 注意：注意v1.end()指向的是最后一个元素的下一个位置，所以访问最后一个元素的正确操作为：v1.end() - 1;

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89

  #include<algorithm> //一般都是前闭后开区间！ //end()指向的是最后一个元素的下一个位置 //front():返回首元素的引用 //back():返回末尾元素的引用 a.front(); a.back(); //sort //对a中的从a.begin()（包括它）到a.end()（不包括它）的元素进行从小到大排列 sort(a.begin(),a.end()); //reverse //对a中的从a.begin()（包括它）到a.end()（不包括它）的元素倒置，但不排列，如a中元素为1,3,2,4,倒置后为4,2,3,1 reverse(a.begin(),a.end()); //find //在a中的从a.begin()（包括它）到a.end()（不包括它）的元素中查找10，若存在返回其在向量中的迭代器位置 find(a.begin(),a.end(),10); vector<int>::iterator it = find(vec.begin(), vec.end(), 6);//auto int it_num=*it; vec.erase(it); int num=it-vec.begin();//返回下标 //accumulate using namespace std; accumulate(num.begin(), num.end(), 0); // std::accumulate 可以很方便地求和,0是初始值 //insert vector<int> v(4); v[0]=2; v[1]=7; v[2]=9; v[3]=5;//此时v为2 7 9 5 v.insert(v.begin(),8);//在最前面插入新元素,此时v为8 2 7 9 5 //is_sorted：判断是否已经是排序了 is_sorted(a,a+5); is_sorted(v.begin(),v.end());//默认升序检查 less<int>() is_sorted(a,a+5,greater<int>()); is_sorted(v.begin(),v.end(),greater<int>());//降序检查,a>b,所以降序 bool cmp(const int & a, const int & b){ return a%10>b%10; } is_sorted(a,a+5,cmp); is_sorted(v.begin(),v.end(),cmp);//自定义排序规则 //vector的赋值 //使用函数assign进行赋值，有两种方式 vector<int > v1;//声明v1 v1.assign(v2.begin(), v2.end());//将v2赋值给v1 vector<int> dp; dp.assign(10, 5);//dp的值是10个5 //直接创建的时候赋值 vector<int> dp(n,value); vector<vector<int>> dp(n,vector<int>(n2,value)); //copy进行赋值，注意此时的original应该开辟了足够的空间，否则会报错 copy(nums.begin(), nums.end(), original.begin()); //vector的尾部插入 vector<int> treeadd; treeadd.pushback(value); treeadd.pop_back();//可以删除最后一个元素,所以vector也可以用作栈 treeadd.emplace(value);//移动插入，减少拷贝次数 //两者的区别 /* ①emplace_back函数的作用是减少对象拷贝和构造次数，是C++11中的新特性，主要适用于对临时对象的赋值。 ②使用push_back函数往容器中增加新元素时，必须要有一个该对象的实例才行，而emplace_back可以不用，它可以直接传入对象的构造函数参数直接进行构造，减少一次拷贝和赋值操作。*/ vector<stu_info> v; v.push_back(stu_info("nginx"));//先构造一个类 vector<stu_info> v; v.emplace_back("redis");//直接传参 //bind2nd比较规则 bind2nd(less<int>(),2);//返回a<2,2nd表示2在比较式子的右边 //swap交换两个向量 vector<int> dp{1,2,3,4,5}; vector<int> dp1(5,10); dp.swap(dp1);

• resize和size和capacity的区别

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

  //resize(n):重新设置向量大小为n，一般改变容量大小capacity以及元素大小size，同时初始值都是0 //capacity():向量的实际容量大小 //size():向量的元素个数 #include <iostream> #include <vector> #include <algorithm> using namespace std; int main() { vector<int> dp; dp.assign(10, 5); dp.resize(0); if (dp.empty()) { cout << "is null" << endl; } cout << "capacity: " << dp.capacity() << endl; cout << "size: " << dp.size() << endl; return 0; }

  

• vector< bool> 并不是一个通常意义上的vector容器

  • 在C++98的时候，就有vector< bool>这个类型了，但是因为当时为了考虑到节省空间的想法，所以vector< bool>里面不是一个Byte一个Byte储存的，它是一个bit一个bit储存的！

  • 因为C++没有直接去给一个bit来操作，所以用operator[]的时候，正常容器返回的应该是一个对应元素的引用，但是对于vector< bool>实际上访问的是一个"proxy reference"而不是一个"true reference"，返回的是"std::vector< bool>:reference"类型的对象。

  • 所以当使用auto类型，会直接改变原bool对应的bit

  • 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

    #include <iostream> #include <vector> #include <algorithm> using namespace std; int main() { vector<bool> c{ false, true, false, true, false }; auto d = c[0]; d = true; for(auto i:c) cout<<i<<" "; cout<<endl; return 0; } //理论认为的输出是01010

  • 

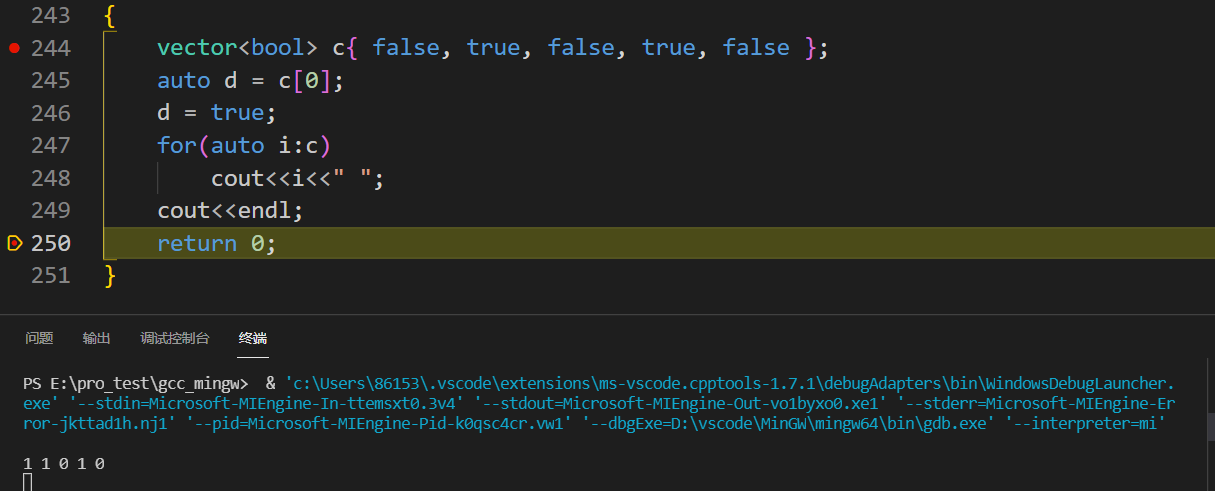
  • 以下强制转为bool才是正确的

    

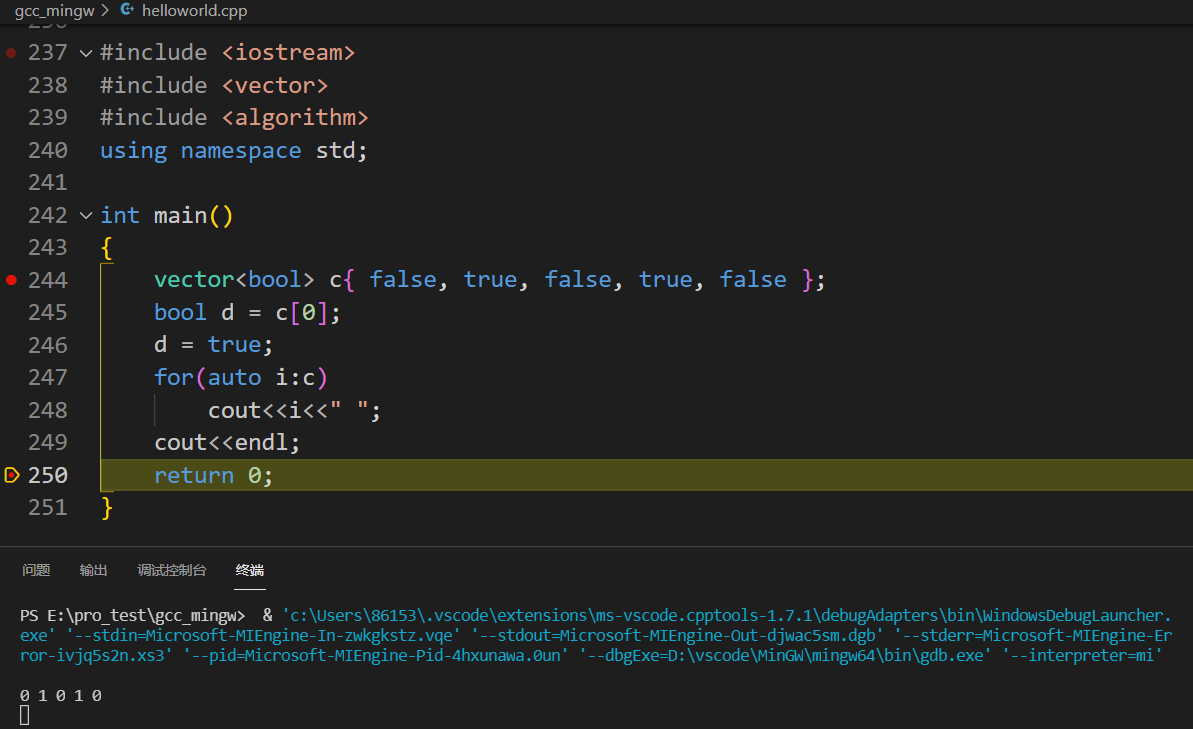
  • 而为什么说vector< bool>不是一个标准容器，就是因为它不能支持一些容器该有的基本操作，诸如取地址给指针初始化操作，因为是bit保存，没有地址可取。

• vector删除元素的方式

• 函数	功能
  pop_back()	删除 vector 容器中最后一个元素，该容器的大小（size）会减 1，但容量（capacity）不会发生改变。
  erase(pos)	删除 vector 容器中 pos 迭代器指定位置处的元素，并返回指向被删除元素下一个位置元素的迭代器。该容器的大小（size）会减 1，但容量（capacity）不会发生改变。
  swap(beg,end)、pop_back()	先调用 swap() 函数交换要删除的目标元素和容器最后一个元素的位置，然后使用 pop_back() 删除该目标元素。
  erase(beg,end)	删除 vector 容器中位于迭代器 [beg,end)，前闭后开，指定区域内的所有元素，并返回指向被删除区域下一个位置元素的迭代器。该容器的大小（size）会减小，但容量（capacity）不会发生改变。
  remove()	删除容器中所有和指定元素值相等的元素，并返回指向最后一个元素下一个位置的迭代器。值得一提的是，调用该函数不会改变容器的大小和容量。
  clear()	删除 vector 容器中所有的元素，使其变成空的 vector 容器。该函数会改变 vector 的大小（变为 0），但不是改变其容量。

  • erase使用例子

    1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

    #include <iostream> #include <vector> #include <algorithm> using namespace std; int main() { vector<int> dp{1, 2, 3, 4, 5}; auto it = dp.begin() + 1; dp.erase(it); for (auto &i : dp) { cout << i << endl; } cout << "现迭代器的指向元素" << *it << endl; return 0; } //输出 /* 1 3 4 5 现迭代器的指向元素3 */

  • swap使用例子——常和pop_back()函数使用。

    1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

    #include <iostream> #include <vector> #include <algorithm> using namespace std; int main() { vector<int> dp{1, 2, 3, 4, 5}; swap(*(std::begin(dp) + 1), *(std::end(dp) - 1)); //等同于 swap(dp[1],dp[4]) for (auto i : dp) { cout << i << endl; } swap(dp[0],dp[3]); return 0; }

  • remove()函数

    • remove() 的实现原理是，在遍历容器中的元素时，一旦遇到目标元素，就做上标记，然后继续遍历，直到找到一个非目标元素，即用此元素将最先做标记的位置覆盖掉，同时将此非目标元素所在的位置也做上标记，等待找到新的非目标元素将其覆盖。因此，将下面程序中 demo 容器的元素全部输出，得到的结果为 1 4 5 4 3 5。

    • 所以remove之后一般要使用erase删除元素，才是真正的删除。

    • 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35

      #include <iostream> #include <vector> #include <algorithm> using namespace std; int main() { vector<int> demo{1, 3, 3, 4, 3, 5}; //交换要删除元素和最后一个元素的位置 auto iter = std::remove(demo.begin(), demo.end(), 3); cout << "size is :" << demo.size() << endl; cout << "capacity is :" << demo.capacity() << endl; //输出剩余的元素 cout << "remove之后: "; for (auto i : demo) { cout << i << " "; } cout << endl; demo.erase(iter, demo.end()); cout << "earse之后: "; for (auto i : demo) { cout << i << " "; } return 0; } //输出结果： /* size is :6 capacity is :6 remove之后: 1 4 5 4 3 5 earse之后: 1 4 5 */

  • clear()函数

    

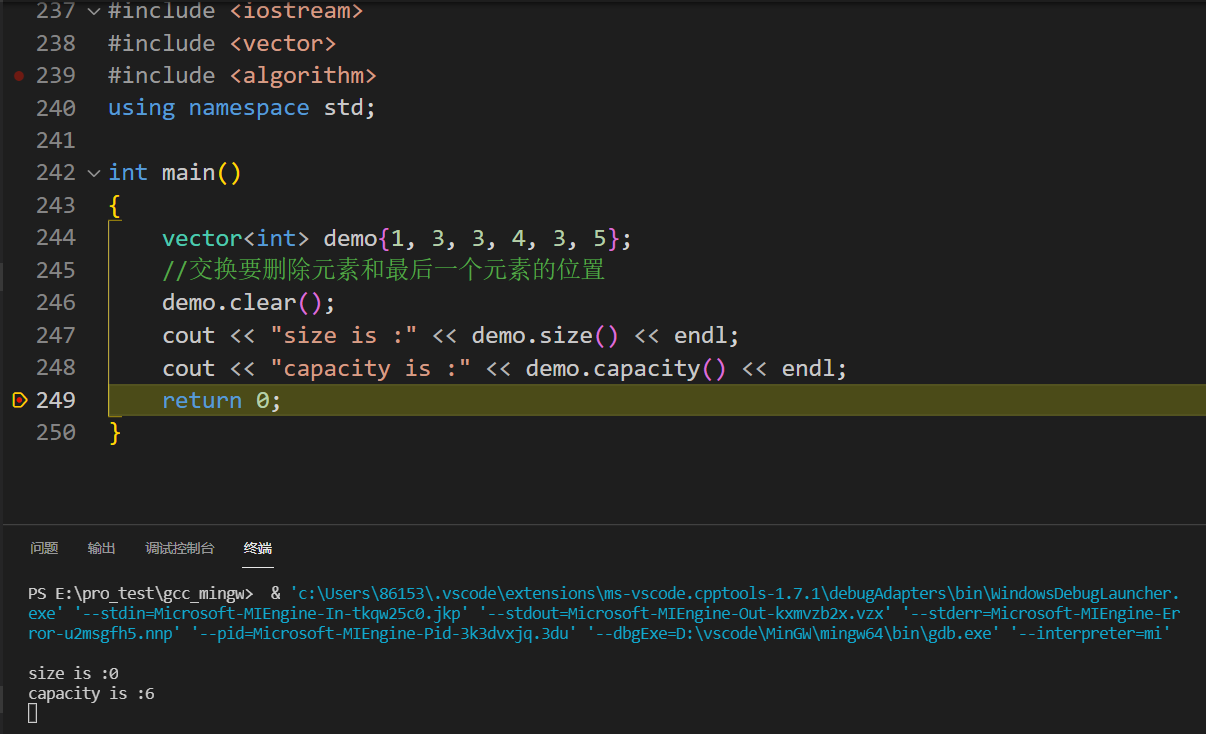
deque 双头队列

• 双端队列

• 1 2 3 4 5 6 7 8 9 10 11

  deque<int> d; d.size(); d.empty(); d.at(); d[]; d.push_back(type); d.push_front(type); d.pop_back();//删除最后一个元素，无返回 d.pop_front();//删除第一个元素，无返回 type=d.front();//返回第一个元素引用 type=d.back();//返回第一个元素的引用

string 字符串

• size()和length()，返回长度，注意用单引号。

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

  string str = "z"; int a = str[0] - 'a'; //a=25； //按字符长度排序 sort(words.begin(),words.end(),[](string &a,string&b){ return a.size()<b.size(); }); //赋值和删除指定字符 string temp; temp.assign(a); temp.erase((temp.begin()+i)); if(b==temp){ return true; } temp.clear(); //返回子串 string substr (size_t pos = 0, size_t len = npos) const;//返回子串

• 字符串的内置查找函数，使用的是朴素算法，而不是KMP算法。记得转为int类型进行判断。

• C++string中find函数是用什么算法实现的？他的时间复杂度如何？实际比手写KMP效率相比如何？

• 1 2 3 4 5 6 7

  int pos = s1.find(s2); if(pos==(int)string::npos){ cout<<"not found"<<endl; }else{ string s3 = s1.substr(pos,s2.size()); cout<<s3<<endl; }

stack 栈

• 栈提供push 和 pop 等等接口，所有元素必须符合先进后出规则，所以栈不提供走访功能，也不提供迭代器(iterator)。 不像是set 或者map 提供迭代器iterator来遍历所有元素。

• 栈是以底层容器完成其所有的工作，对外提供统一的接口，底层容器是可插拔的（也就是说我们可以控制使用哪种容器来实现栈的功能）。

• 所以STL中栈往往不被归类为容器（container），而被归类为container adapter（容器适配器）。

• 栈的底层实现可以是vector，deque，list 都是可以的， 主要就是数组和链表的底层实现。

• 我们常用的SGI STL，如果没有指定底层实现的话，默认是以deque为缺省情况下栈的低层结。

• deque是一个双向队列，只要封住一段，只开通另一端就可以实现栈的逻辑了。 SGI STL中 队列底层实现缺省情况下一样使用deque实现的。

• SGI STL 是Linux默认的STL。

• 我们也可以指定vector为栈的底层实现，初始化语句如下：std::stack<int, std::vector<int> > third; // 使用vector为底层容器的栈

• LIFO，后进先出

  1 2 3 4 5

  s.push(type); type=s.top();//返回栈顶元素，不推出 s.pop();//无返回值，推出栈顶元素 s.empty(); s.size();

queue 队列

• STL中队列也不被归类为容器，而被归类为container adapter(容器适配器)。

• SGI STL中队列一样是以deque为缺省情况下的底部结构。

• 也可以指定list或vector为底层实现：

• 1 2	std::queue<int,std::list<int>> std11; std::queue<int,std::vector<int>> std11;

• LILO

• 1 2 3 4

  q.push(type); q.pop();//退出第一个元素 type=q.front(); type=q.back();

ListNode 链表

• 分类

  • 单链表
  • 双链表：前驱后继
  • 循环链表

• 力扣一般的单链表定义，不推荐使用STL的list，slist

  1 2 3 4 5 6 7 8 9 10 11

  //单链表 struct ListNode{ int val;//节点上存储的元素 ListNode *next;//指向下一节点的指针 ListNode(int x):val(x),next(NULL){}//节点上的构造函数 }; ListNode* head = new ListNode(5); //删除 head->next=NULL; delete head;

list 双向链表

• 该容器的底层是以双向链表的形式实现的。这意味着，list 容器中的元素可以分散存储在内存空间里，而不是必须存储在一整块连续的内存空间中。

• list 容器中各个元素的前后顺序是靠指针来维系的，每个元素都配备了 2 个指针，分别指向它的前一个元素和后一个元素。其中第一个元素的前向指针总为 null，因为它前面没有元素；同样，尾部元素的后向指针也总为 null。

• 基于这样的存储结构，list 容器具有一些其它容器（array、vector 和 deque）所不具备的优势，即它可以在序列已知的任何位置快速插入或删除元素（时间复杂度为O(1)）。并且在 list 容器中移动元素，也比其它容器的效率高。

• 使用 list 容器的缺点是，它不能像 array 和 vector 那样，通过位置直接访问元素。举个例子，如果要访问 list 容器中的第 6 个元素，它不支持list[6]这种语法格式，正确的做法是从容器中第一个元素或最后一个元素开始遍历容器，直到找到该位置。

• 成员函数	功能
  begin()	返回指向容器中第一个元素的双向迭代器。
  end()	返回指向容器中最后一个元素所在位置的下一个位置的双向迭代器。
  rbegin()	返回指向最后一个元素的反向双向迭代器。
  rend()	返回指向第一个元素所在位置前一个位置的反向双向迭代器。
  cbegin()	和 begin() 功能相同，只不过在其基础上，增加了 const 属性，不能用于修改元素。
  cend()	和 end() 功能相同，只不过在其基础上，增加了 const 属性，不能用于修改元素。
  crbegin()	和 rbegin() 功能相同，只不过在其基础上，增加了 const 属性，不能用于修改元素。
  crend()	和 rend() 功能相同，只不过在其基础上，增加了 const 属性，不能用于修改元素。
  empty()	判断容器中是否有元素，若无元素，则返回 true；反之，返回 false。
  size()	返回当前容器实际包含的元素个数。
  max_size()	返回容器所能包含元素个数的最大值。这通常是一个很大的值，一般是 232-1，所以我们很少会用到这个函数。
  front()	返回第一个元素的引用。
  back()	返回最后一个元素的引用。
  assign()	用新元素替换容器中原有内容。
  emplace_front()	在容器头部生成一个元素。该函数和 push_front() 的功能相同，但效率更高。
  push_front()	在容器头部插入一个元素。
  pop_front()	删除容器头部的一个元素。
  emplace_back()	在容器尾部直接生成一个元素。该函数和 push_back() 的功能相同，但效率更高。
  push_back()	在容器尾部插入一个元素。
  pop_back()	删除容器尾部的一个元素。
  emplace()	在容器中的指定位置插入元素。该函数和 insert() 功能相同，但效率更高。
  insert()	在容器中的指定位置插入元素。
  erase()	删除容器中一个或某区域内的元素。
  swap()	交换两个容器中的元素，必须保证这两个容器中存储的元素类型是相同的。
  resize()	调整容器的大小。
  clear()	删除容器存储的所有元素。
  splice()	将一个 list 容器中的元素插入到另一个容器的指定位置。
  remove(val)	删除容器中所有等于 val 的元素。
  remove_if()	删除容器中满足条件的元素。
  unique()	删除容器中相邻的重复元素，只保留一个。
  merge()	合并两个事先已排好序的 list 容器，并且合并之后的 list 容器依然是有序的。
  sort()	通过更改容器中元素的位置，将它们进行排序。
  reverse()	反转容器中元素的顺序。

• list 创建——5种方式

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

  //1.创建一个没有任何元素的空 list 容器 std::list<int> dp; //2.创建一个包含 n 个元素的 list 容器 std::list<int> values(10);//创建10个元素的list容器 //3.创建一个包含 n 个元素的 list 容器，并为每个元素指定初始值 std::list<int> values(10, 5);//创建10个元素，初始值都是5 //4.在已有 list 容器的情况下，通过拷贝该容器可以创建新的 list 容器 //注意两个list的类型要相同，也可以使用assign std::list<int> value1(10); std::list<int> value2(value1); list<int> dp{11,12,13,14,15}; list<int> dp3; dp3.assign(dp.rbegin(), dp.rend()); //5.通过拷贝其他类型容器（或者普通数组）中指定区域内的元素，可以创建新的 list 容器。 //拷贝普通数组，创建list容器 int a[] = { 1,2,3,4,5 }; std::list<int> values(a, a+5); //拷贝其它类型的容器，创建 list 容器 vector<int> arr1{ 11, 12, 13, 14, 15 }; std::list<int> dp(arr1.begin(), arr1.end());

• list的访问和插入，不允许随机访问，只能从头到尾遍历

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31

  #include <iostream> #include <list> #include <algorithm> using namespace std; int main() { list<double> dp{1.5, 2.5, 3.5, 4.5}; dp.insert(dp.begin(),5); cout << "正序" << endl; for (auto i = dp.begin(); i != dp.end(); ++i) { cout << *i << " "; } cout << endl << "反序" << endl; for (auto i = dp.rbegin(); i != dp.rend(); ++i) { cout << *i << " "; } return 0; } //输出 /* 正序 5 1.5 2.5 3.5 4.5 反序 4.5 3.5 2.5 1.5 5 */

• list的删除

• 成员函数	功能
  pop_front()	删除位于 list 容器头部的一个元素。
  pop_back()	删除位于 list 容器尾部的一个元素。
  erase()	该成员函数既可以删除 list 容器中指定位置处的元素，也可以删除容器中某个区域内的多个元素。
  clear()	删除 list 容器存储的所有元素。
  remove(val)	删除容器中所有等于 val 的元素。
  unique()	删除容器中相邻的重复元素，只保留一份。
  remove_if()	删除容器中满足条件的元素。

  • remove(val)（注意和vector的不同的）

    

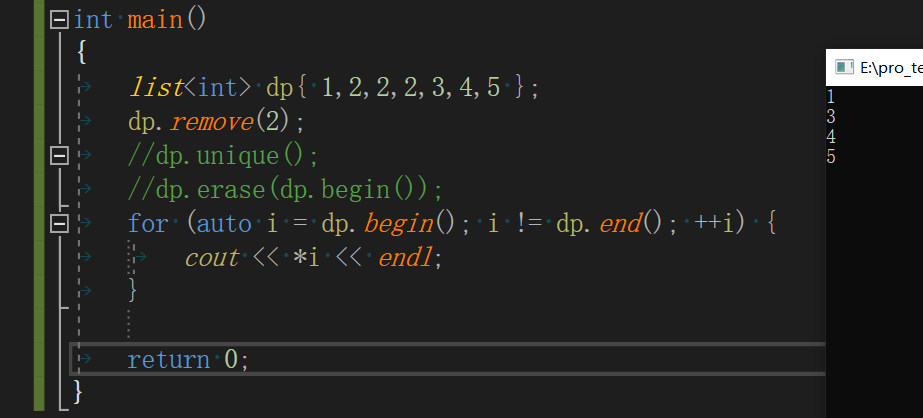
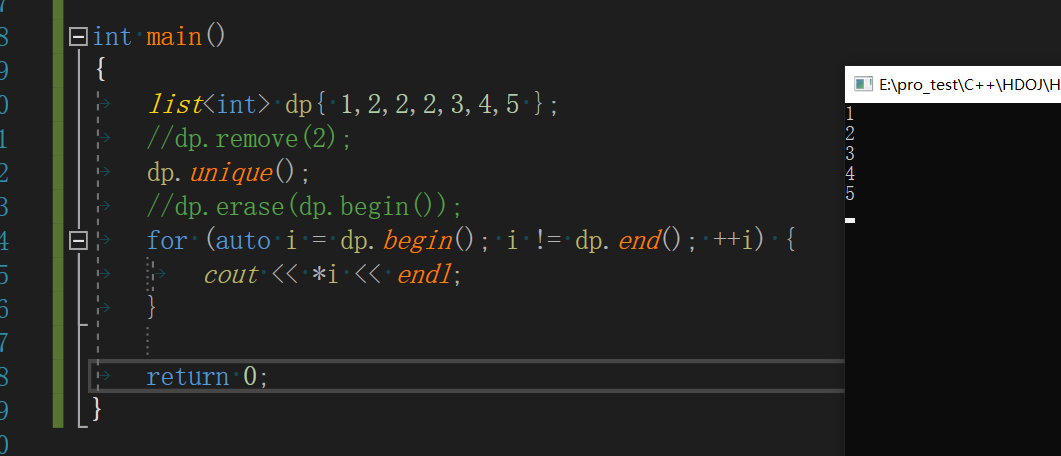
  • unique用法

    

  • earse用法（注意输入都是迭代器）

    

哈希表

• hash tabel，也称为散列表

• 当我们遇到了要快速判断一个元素是否出现集合里的时候，就要考虑哈希法。

  但是哈希法也是牺牲了空间换取了时间，因为我们要使用额外的数组，set或者是map来存放数据，才能实现快速的查找。

  如果在做面试题目的时候遇到需要判断一个元素是否出现过的场景也应该第一时间想到哈希法！

• hash function ，也就是哈希函数。

• 当我们想使用哈希法来解决问题的时候，我们一般会选择如下三种数据结构。

  • 数组
  • set （集合）
  • map(映射)

• set

  集合	底层实现	是否有序	数值是否可以重复	能否更改数值	查询效率	增删效率
  std::set	红黑树	有序	否	否	O(logn)	O(logn)
  std::multiset	红黑树	有序	是	否	O(logn)	O(logn)
  std::unordered_set	哈希表	无序	否	否	O(1)	O(1)

  std::unordered_set底层实现为哈希表，std::set 和std::multiset 的底层实现是红黑树，红黑树是一种平衡二叉搜索树，所以key值是有序的，但key不可以修改，改动key值会导致整棵树的错乱，所以只能删除和增加。

• map

  映射	底层实现	是否有序	数值是否可以重复	能否更改数值	查询效率	增删效率
  std::map	红黑树	key有序	key不可重复	key不可修改	O(logn)	O(logn)
  std::multimap	红黑树	key有序	key可重复	key不可修改	O(logn)	O(logn)
  std::unordered_map	哈希表	key无序	key不可重复	key不可修改	O(1)	O(1)

  std::unordered_map 底层实现为哈希表，std::map 和std::multimap 的底层实现是红黑树。同理，std::map 和std::multimap 的key也是有序的（这个问题也经常作为面试题，考察对语言容器底层的理解）。

• 当我们要使用集合来解决哈希问题的时候，优先使用unordered_set，因为它的查询和增删效率是最优的，如果需要集合是有序的，那么就用set，如果要求不仅有序还要有重复数据的话，那么就用multiset。

• 从本质上来讲，物理存储结构只有数组和链表两种。其他的数据结构都是抽象结构。而哈希表的底层实现是数组，数组是通过下标索引访问的，那哈希表就要生成一个索引，为每一个元素分配唯一的索引，而生成这个索引的工具就叫做“哈希函数”，每一个存放数据的位置叫做“桶”。

• 虽然std::set、std::multiset 的底层实现是红黑树，不是哈希表，但是std::set、std::multiset 依然使用哈希函数来做映射，只不过底层的符号表使用了红黑树来存储数据，所以使用这些数据结构来解决映射问题的方法，我们依然称之为哈希法。 map也是一样的道理。

• unordered_set在C++11的时候被引入标准库了，而hash_set并没有，所以建议还是使用unordered_set比较好，这就好比一个是官方认证的，hash_set，hash_map 是C++11标准之前民间高手自发造的轮子。

• 常见count、erase函数

• unordered_set< int> dict(to_delete.begin(), to_delete.end());

• 为了便于寻找待删除节点，可以建立一个哈希表方便查找。

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37

  set<int> s; s.insert(10); //默认从小到大 //从大到小可以是 greater<int>() //set不允许有重复的元素 //multiset允许有 //erase //删除单个元素 #include<iostream> #include<set> using namespace std; int main() { set<int>st; for(int i=1;i<=3;i++) st.insert(i); st.erase(st.find(2));//删除元素2 //此处直接st.erase(2)也可以 for(set<int>::iterator it=st.begin();it!=st.end();it++) cout<<*it<<" "<<endl; return 0; } #include<iostream> #include<set> using namespace std; int main() { set<int>st; set<int>::iterator it; for(int i=1;i<=3;i++) st.insert(i); st.erase(st.find(2),st.end());//删除元素2至set末尾之间的元素 for(it=st.begin();it!=st.end();it++) cout<<*it<<endl; return 0; }

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56

  // 定义一个map对象 map<int, string> mapStudent; // 第一种 用insert函數插入pair mapStudent.insert(pair<int, string>(000, "student_zero")); // 第二种 用insert函数插入value_type数据 mapStudent.insert(map<int, string>::value_type(001, "student_one")); // 第三种 用"array"方式插入 mapStudent[123] = "student_first"; mapStudent[456] = "student_second"; /* C++ maps是一种关联式容器，包含“关键字/值”对 begin() 返回指向map头部的迭代器 clear(） 删除所有元素 count() 返回指定元素出现的次数, (帮助评论区理解： 因为key值不会重复，所以只能是1 or 0) empty() 如果map为空则返回true end() 返回指向map末尾的迭代器 equal_range() 返回特殊条目的迭代器对 erase() 删除一个元素 find() 查找一个元素 get_allocator() 返回map的配置器 insert() 插入元素 key_comp() 返回比较元素key的函数 lower_bound() 返回键值>=给定元素的第一个位置 max_size() 返回可以容纳的最大元素个数 rbegin() 返回一个指向map尾部的逆向迭代器 rend() 返回一个指向map头部的逆向迭代器 size() 返回map中元素的个数 swap() 交换两个map upper_bound() 返回键值>给定元素的第一个位置 value_comp() 返回比较元素value的函数 map只是键值进行排序且唯一，value不唯一，不排序，是key的映射 */

• 1 2 3 4 5 6 7 8

  unordered_set<int> dp; //以下是常见用法，value是键值 dp.insert(value); dp.count(value); dp.erase(value); //erase还可以通过迭代器 dp.erase(iterator);//删除迭代器所指的键值 dp.erase(begin,end);//删除begin和end之间迭代器的键值，前闭后开

map的三种遍历方式

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51

  #include<iostream> #include<string> #include<map> using namespace std; int main(){ map<int,string> m{}; m[0]="aaa"; m[1]="bbb"; m[2]="ccc"; map<int,string>::iterator it; //方式一，加强for转成pair cout<<"method 1:"<<endl; for(auto &t : m){ cout<<"key:"<<t.first<<" value:"<<t.second<<endl; } //方式二 cout<<"method 2:"<<endl; for(auto iter = m.begin(); iter != m.end(); ++iter){ cout<<"key:"<<iter->first<<" value:"<<iter->second<<endl; } //第三种 cout<<"method 3:"<<endl; auto iter=m.begin(); while(iter != m.end()){ cout<<"key:"<<iter->first<<" value:"<<iter->second<<endl; ++iter; } } /*输出结果 method 1: key:0 value:aaa key:1 value:bbb key:2 value:ccc method 2: key:0 value:aaa key:1 value:bbb key:2 value:ccc method 3: key:0 value:aaa key:1 value:bbb key:2 value:ccc */

unordered_set 的哈希自定义类型

• 1 2 3 4 5

  template < class Key, //容器中存储元素的类型 class Hash = hash<Key>, //确定元素存储位置所用的哈希函数 class Pred = equal_to<Key>, //判断各个元素是否相等所用的函数 class Alloc = allocator<Key> //指定分配器对象的类型 > class unordered_set;

• 自定义类型，需要重新定义hash函数，还有判断重复的equal_to函数。

• 有三种自定义方式

• 第一种，在std命名空间重载哈希函数，相等函数重载。

• 第二种，哈希函数和相等函数重载。

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129

  #include <iostream> #include <math.h> #include <unordered_set> using namespace std; //显示模板化 template<typename Container> void display(const Container &con) { for (auto &elem:con) { cout << elem << " "; } } //自定义数据类型 class Point { public: Point(int ix = 0, int iy = 0) : _ix(ix), _iy(iy) { } double getDistance() const { //平方和库函数 return hypot(_ix, _iy); } int getX() const { return _ix; } int getY() const { return _iy; } ~Point() { } //重载输出符合 friend std::ostream &operator<<(std::ostream &os, const Point &rhs); private: int _ix; int _iy; }; std::ostream &operator<<(std::ostream &os, const Point &rhs) { os << "(" << rhs._ix << ", " << rhs._iy << ")"; return os; } //拓展std命名空间 namespace std { //模板全特化，才能进行hash函数的重载 template<> struct hash<Point> { //自定义哈希函数,参照官方例子来写 size_t operator()(const Point &rhs) const { return ((rhs.getX() << 1) ^ (rhs.getY() << 2)); } }; } //重载==运算符，用于自定义的equal_to,对象与对象进行比较，用于去重 bool operator==(const Point &lhs, const Point &rhs) { return (lhs.getX() == rhs.getX()) && (lhs.getY() == rhs.getY()); } void test01() { //1.扩展命名空间形式来重写Point的哈希函数，重载函数公用 unordered_set<Point> number = { Point(1, 2), Point(1, -2), Point(-1, 3), Point(1, 2), Point(3, 5), Point(7, 8), }; display(number); cout << endl; number.insert(Point(1, 3)); display(number); cout << endl; } struct hashPoint { size_t operator()(const Point &rhs) const { //自定义哈希函数 return ((rhs.getX() << 1) ^ (rhs.getY() << 2)); } }; void test02() { //2.直接以函数对象的形式来重写Point的哈希函数 unordered_set<Point, hashPoint> number = { Point(1, 2), Point(1, -2), Point(-1, 3), Point(1, 2), Point(3, 5), Point(7, 8), }; display(number); cout << endl; number.insert(Point(1, 3)); display(number); cout << endl; } int main() { cout << "template used:" << endl; test01(); cout << endl; cout << "function used:" << endl; test02(); return 0; } /*输出结果 template used: (7, 8) (3, 5) (-1, 3) (1, -2) (1, 2) (1, 3) (7, 8) (3, 5) (-1, 3) (1, -2) (1, 2) function used: (7, 8) (3, 5) (-1, 3) (1, -2) (1, 2) (1, 3) (7, 8) (3, 5) (-1, 3) (1, -2) (1, 2) */

• 第三种，类里面直接重载相等函数，类外重载哈希函数

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95

  #include <iostream> #include <math.h> #include <unordered_set> using namespace std; //显示模板化 template<typename Container> void display(const Container &con) { for (auto &elem:con) { cout << elem << " "; } } //自定义数据类型 class Point { public: Point(int ix = 0, int iy = 0) : _ix(ix), _iy(iy) { } bool operator==(const Point& rc) const //重载== { return _ix == rc.getX() && _iy == rc.getY(); } double getDistance() const { //平方和库函数 return hypot(_ix, _iy); } int getX() const { return _ix; } int getY() const { return _iy; } ~Point() { } //重载输出符合 friend std::ostream &operator<<(std::ostream &os, const Point &rhs); private: int _ix; int _iy; }; //重载哈希函数 struct hashPoint { //参数为const，函数也是const size_t operator()(const Point &rhs) const { //自定义哈希函数 return ((rhs.getX() << 1) ^ (rhs.getY() << 2)); } }; std::ostream &operator<<(std::ostream &os, const Point &rhs) { os << "(" << rhs._ix << ", " << rhs._iy << ")"; return os; } void test03() { //1.扩展命名空间形式来重写Point的哈希函数，重载函数公用 unordered_set<Point,hashPoint> number = { Point(1, 2), Point(1, -2), Point(-1, 3), Point(1, 2), Point(3, 5), Point(7, 8), }; display(number); cout << endl; number.insert(Point(1, 3)); display(number); cout << endl; } int main() { cout << "inner class used:" << endl; test03(); return 0; } /*输出结果 inner class used: (7, 8) (3, 5) (-1, 3) (1, -2) (1, 2) (1, 3) (7, 8) (3, 5) (-1, 3) (1, -2) (1, 2) */

• 综述，以后个人约定用类内定义相等函数，类外定义哈希函数。

priority_queue 优先队列

常见优先级判断greater和less的使用

• #include < functional> 头文件引用

• sort默认是升序，即less

• greater的用法——从大到小排序

  1 2 3 4 5 6 7 8 9 10 11 12

  #include <bits/stdc++.h> using namespace std; int main() { vector<string> dp; dp = { "abc","ade","dfs","frg","fab" }; sort(dp.begin(), dp.end(), greater<string>()); for (auto &i : dp) { cout << i << endl; } return 0; }

  

• less的用法——从小到大排序

  1 2 3 4 5 6 7 8 9 10 11 12

  #include <bits/stdc++.h> using namespace std; int main() { vector<string> dp; dp = { "abc","ade","dfs","frg","fab" }; sort(dp.begin(), dp.end(), less<string>()); for (auto &i : dp) { cout << i << endl; } return 0; }

  

二叉堆以及堆排序

二叉堆的概述——以最小堆为例

• 1.二叉堆的插入

  • 插入尾结点。在数组尾部插入新的节点，如果该节点的值大于父节点，则交换该节点和父节点，依次上浮。时间复杂度是$(O(log_n))$ 。

• 2.二叉堆的删除

  • 删除堆顶元素，把尾结点和堆顶的值交换，下沉堆顶元素的值。具体做法是，如果堆顶元素大于左右孩子的最小元素，则交换堆顶元素和左右孩子最小的元素，直到无法下沉为止。时间复杂度是$(O(log_n))$ 。

• 3.二叉树的构建

  • 二叉树的构建其实就是堆顶元素的下沉操作。从最后一个非叶子节点开始进行下沉操作，直到堆顶元素完成下沉操作。
  • 时间复杂度是$(O(n))$ 。
  • 证明方法如下：
  • 假设有n个节点，节点下表从0开始，树高从0开始，那么树高为 $log_2n$
  • 假设根节点的高度为0，高度为h，那么每层高度x包含的元素个数为 $2^x$，x从0到h。
  • 构建堆的过程是自下而上，对于每层非叶子节点需要调整的次数为h-x，因此很明显根节点需要调整(h-0)次，第一层节点需要调整(h-1)次，最下层非叶子节点需要调整1次。
  • 不妨假设是满二叉树，那么最大时间复杂度为 $s = 1×2^{(h-1)} + 2×2^{(h-2)}+……+h×2^0$ 。
  • 以上是等差和等比数列的乘积，运用错位相减法，得出 $ 2n - 2 - log_2(n)$，近似的时间复杂度就是$O(n)$ 。

• 二叉堆是一个完全二叉树，储存方式为顺序存储，即存储在数组里。下标从0开始。树的高度从0开始设为x，每一层最多节点个数为$(x^2)$ 。

• 如何定位左右孩子，依靠数组下标实现，从0开始，左孩子下标为2*parent+1，右孩子为2*parent+2。

• 最大堆：任何一个父节点的值，都大于或等于左孩子和右孩子的节点的值，堆顶为最大值

• 最小堆：任何一个父节点的值，都小于或等于左孩子和右孩子的节点的值，堆顶为最小值

• 注意堆和二叉查找树的区别

• 三种操作：

  • 尾结点插入——上浮
  • 堆顶删除——下沉
  • 二叉堆的构建（依次从最大非叶子节点下沉）

• 堆排序基本思想

  • a.将无序序列构建成一个堆，根据升序降序需求选择大顶堆或小顶堆;
  • b.将堆顶元素与末尾元素交换，将最大元素"沉"到数组末端;
  • c.重新调整结构，使其满足堆定义，然后继续交换堆顶元素与当前末尾元素，反复执行b+c步骤，直到整个序列有序。

• 最大优先队列：无论入队顺序如何，当前最大元素都会优先出队，基于最大堆实现的。

• 最小优先队列：无论入队顺序如何，当前最小元素都会优先出队，基于最小堆实现的。

具体函数用法

• priority_queue：优先队列，底层是使用堆来实现的。优先队列中，队首元素一定是当前队列中优先级最高的哪一个。

• 默认是大顶堆。注意和sort相反。

• priority_queue<Type, Container, Functional> Type 就是数据类型，Container 就是容器类型（Container必须是用数组实现的容器，比如vector,deque等等，但不能用 list。STL里面默认用的是vector），Functional 就是比较的方式。

  当需要用自定义的数据类型时才需要传入这三个参数，使用基本数据类型时，只需要传入数据类型，默认是大顶堆。

• 使用优先队列，要加头文件#include< queue>和using namespace std;

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

  /* 1、push() push(x)：将x入队，时间复杂度为O(logN)，N为优先队列中元素个数。 2、top() top()：获得堆顶元素，时间复杂度为O(1) 3、pop() pop()：让堆顶元素出队，时间复杂度为O(logN) 4、empty() empty()：检测优先队列是否为空，返回bool值，true为空，false非空 5、size() size()：返回优先队列中的元素个数。 */

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

  priority_queue<int> pq; priority_queue<int,vector<int>,less<int>> pq; /* 　　vector<int>:承载底层数据结构堆Heap的容器 　　如果第一个参数是double，那么第二个也对应是double 　　less<int>：是对第一个参数的比较类，less<int>表示的数组大的优先级越大。默认是less 　　greater<int>：表示数字小的优先级越大 */ priority_queue<int,vector<int>,greater<int>> pq; 　　//优先队列总是把最小的元素放在队首。注意和sort相反 priority_queueK<int,vector<int>,less<int>> pq; 　　//优先队列总是把最大的元素放在队首。注意和sort相反 priority_queue<int> a; //等同于 priority_queue<int, vector<int>, less<int> > a;

自定义比较函数

• 有两种方式

• （1）结构体中重载<符号，注意声明函数为const。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39

  #include <iostream> #include <vector> #include <algorithm> #include <queue> #include <numeric> using namespace std; class Edge{ public: int start; int end; int cost; Edge(int start1 ,int end1 ,int cost1):start(start1),end(end1),cost(cost1){} bool operator<(const Edge& E1) const { //>表示小顶堆，<表示大顶堆 return this->cost > E1.cost; } }; int main() { //less调用了重载运算符 < ，所以重新定义之后 priority_queue<Edge,vector<Edge>,less<Edge>> pq; Edge temp(1,2,3); Edge temp2(1,2,4); Edge temp5(1,5,6); pq.push(temp); pq.push(temp2); auto i=pq.top(); cout<<i.cost<<endl; pq.push(temp5); i=pq.top(); cout<<i.cost<<endl; return 0; } //输出——符合小顶堆的含义 3 3

• 第二种声明自定义比较函数的方式是创建一个结构体，重载()符号

  • 注意：> 表示小顶堆， < 表示大顶堆

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44

  #include <iostream> #include <vector> #include <algorithm> #include <queue> #include <numeric> using namespace std; class Edge{ public: int start; int end; int cost; Edge(int start1 ,int end1 ,int cost1):start(start1),end(end1),cost(cost1){} }; struct cmp { bool operator()(const Edge& f1, const Edge& f2) { //小顶堆 return f1.cost>f2.cost; } }; int main() { priority_queue<Edge,vector<Edge>,cmp> pq; Edge temp(1,2,3); Edge temp2(1,2,1); Edge temp5(1,5,4); pq.push(temp); pq.push(temp2); auto i=pq.top(); cout<<i.cost<<endl; pq.push(temp5); i=pq.top(); cout<<i.cost<<endl; return 0; } //输出——符合小顶堆 1 1

set、map和priority_queue的区别

• set

  1 2 3

  set<int> s;//默认升序,相当于 set<int,less<int> >。 set<int,less<int> > s; //该容器是按升序方式排列元素。 set<int,greater<int>> s; //该容器是按降序方式排列元素。

• map

  1 2 3

  map<T1,T2> m;//默认按键的升序方式排列元素,相当于下方的less map<T1,T2,less<T1> > m; //该容器是按键的升序方式排列元素。 map<T1,T2,greater<T1>> m; //该容器是按键的降序方式排列元素。

• priority_queue

  1 2 3

  priority_queue<int> p; //默认降序， 大顶堆，队头元素最大 priority_queue<int, vector<int>, less<int> > p; //相当于默认 priority_queue<int, vector<int>, greater<int>> p; //升序，最小值优先级队列，小顶堆

• set和map默认升序即从小到大； 可通过加一个参数greater<>改变成降序； 而priorty_queue默认降序即从大到小； 需通过加两个参数vector<>, greater<>改变成升序； 改变的相同点是都需要greater<>这个参数来改变； 不同点在于优先队列还需多一个vector<>参数在前面。

• set和map从小到大； priorty_queue从大到小； 都需要greater<>来改变； 优先队列还需vector<>参数在前面。

• set<pair<int, string>>可以对int进行排序，默认是小的，第一个相等就排序第二个

• set<pair<int,int>> 一样可以，但都是默认是小排序。

• 但是注意unordered_set<pair> 是不行的，需要自定义哈希函数以及相等的函数。

OJ 输入输出

• 关于cin：默认是以空格或者回车分开的

  1	cin>>a>>b;//输入的时候以空格分开，或是输入一个回车一个

• cin、cin.get()、cin.getline()、getline()的区别

• 问题1：关于cin.get() 的输入数字换行

  • 

  • 1 2 3 4 5 6 7 8 9 10 11 12

    #include<iostream> using namespace std; int main() { int sum = 0, a; while (cin >> a) { sum += a; if (cin.get() == '\n') { // 判断数据之间的间隔是不是换行 cout << sum << endl; sum = 0; } } }

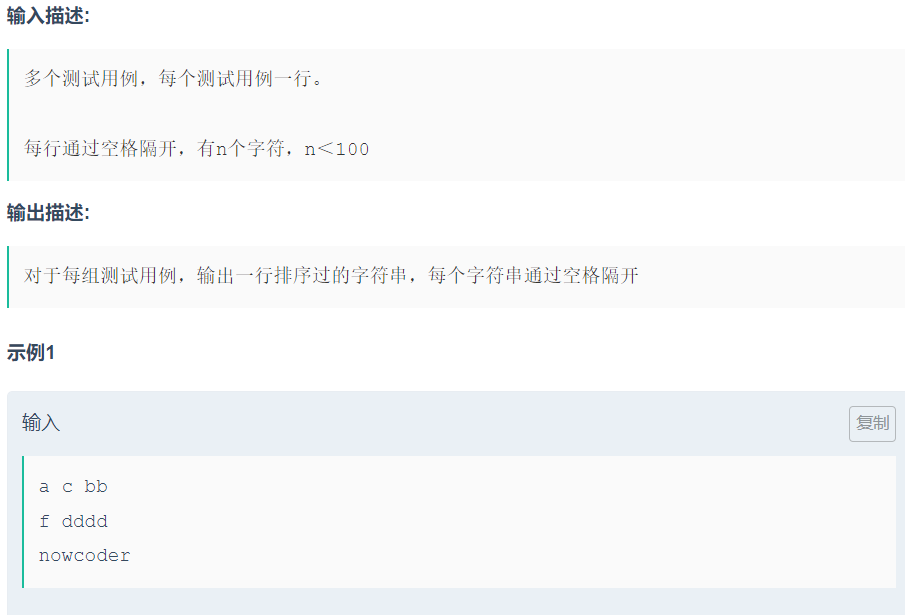
• 问题2：关于cin.get() 的输入字符串换行

  • 

  • 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

    #include <iostream> #include <string> #include <vector> #include <algorithm> using namespace std; int main() { string str; vector<string> dp; while (cin >> str) { dp.push_back(str); if (cin.get() == '\n') { // 判断数据之间的间隔是不是换行 sort(dp.begin(), dp.end()); for (int i = 0; i < dp.size()-1; ++i) { cout << dp[i] << ' '; } cout << dp[dp.size() - 1]<<endl; dp.clear(); } } return 0; }

• 问题3：关于cin.get() 的输入字符串以逗号分隔和换行

  • 

  • 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32

    #include<iostream> #include<string> #include<vector> #include<algorithm> using namespace std; int main(){ string s; vector<string> ans; char a; while(cin.get(a)){ // 一个一个字符地读 if(a!=','&&a!='\n'){ s = s + a; } if(a==','){ ans.push_back(s); s.clear(); } // 一组数据结束 if(a=='\n'){ ans.push_back(s); s.clear(); int n = ans.size(); sort(ans.begin(),ans.end()); for(int i=0;i<n-1;i++){ cout << ans[i] << ","; } cout << ans[n-1] << endl; ans.clear(); } } return 0; }

利用getline函数输入字符串数组（注意点）

• https://blog.csdn.net/weixin_44915226/article/details/109007465

• 在 cin >> n; 的时候，将输入的 2 赋给了 n，但是，换行符还在输入流中，所以在下面第一次使用 getline 的时候，其实是将换行符输入给了变量，这样就导致最后一个字符串没有被输入进去。解决方法是在 cin >> n; 后面加一个 cin.ignore() 或 cin.get()。

  第三种方法是将 getline(cin, timePoints_item); 改成了 cin >> timePoints_item;。这样也能通过。

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

  #include <bits/stdc++.h> using namespace std; int main(int argc, char** argv) { int n; cin>>n; string arr[n]; for(int i=0;i<n;i++){ getline(cin,arr[i]); } for(int i=0;i<n;i++){ cout<<arr[i]<<endl; } return 0; }

• 两种修改方法

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

  #include <bits/stdc++.h> using namespace std; int main(int argc, char** argv) { int n; cin>>n; // cin.get(); cin.ignore(); string arr[n]; for(int i=0;i<n;i++){ getline(cin,arr[i]); } for(int i=0;i<n;i++){ cout<<arr[i]<<endl; } return 0; }

• 或者直接用cin

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

  #include <bits/stdc++.h> using namespace std; int main(int argc, char** argv) { int n; cin>>n; string arr[n]; for(int i=0;i<n;i++){ cin>>arr[i]; } for(int i=0;i<n;i++){ cout<<arr[i]<<endl; } return 0; }

STL算法库函数 < algorithm>

• for_each

  • for_each(iterator begin, iterator end, proc op):

  • 在begin和end前闭后开区间的每个元素都调用进程op（[begin,end)）

  • op和lambda表达式一起使用有很高的简洁性和效率。

• 1 2 3 4 5 6 7 8

  for_each(myvector.begin(), myvector.end(), [](int x) { cout << x*x << endl; }); //按vector的第二个元素大小，从小到大排序。vector<vector<int>>& intervals sort(intervals.begin(), intervals.end(), [](vector<int> a, vector<int> b) { return a[1] < b[1]; });

• 函数名	解释
  max()	返回两个元素中值最大的元素
  min()	返回两个元素中值最小的元素
  abs()	返回元素绝对值
  next_permutation	返回给定范围中的元素组成的下一个按字典序的排列

• next_permutation产生全排列（除了当前队列，可以使用do while产生全排列）

• fill()：fill() 可以把数组或容器中的某一段区间赋为某个相同的值。和memset不同，这里的赋值可以使数组类型对应范围中的任意值。同样是前闭后开区间，[begin,end)。

• lower_bound 和 upper_bound()

  • lower_bound 和 upper_bound()需要用在一个有序数组或容器中。

  • lower_bound( )和upper_bound( )都是利用二分查找的方法在一个排好序的数组中进行查找的。

  • 在从小到大的排序数组中，

    lower_bound( begin,end,num)：从数组的begin位置到end-1位置二分查找第一个大于或等于num的数字，找到返回该数字的地址，不存在则返回end。通过返回的地址减去起始地址begin,得到找到数字在数组中的下标。

    upper_bound( begin,end,num)：从数组的begin位置到end-1位置二分查找第一个大于num的数字，找到返回该数字的地址，不存在则返回end。通过返回的地址减去起始地址begin,得到找到数字在数组中的下标。

  • 在从大到小的排序数组中，重载lower_bound()和upper_bound()

    lower_bound( begin,end,num,greater() ):从数组的begin位置到end-1位置二分查找第一个小于或等于num的数字，找到返回该数字的地址，不存在则返回end。通过返回的地址减去起始地址begin,得到找到数字在数组中的下标。

    upper_bound( begin,end,num,greater() ):从数组的begin位置到end-1位置二分查找第一个小于num的数字，找到返回该数字的地址，不存在则返回end。通过返回的地址减去起始地址begin,得到找到数字在数组中的下标。

  • 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

    #include<bits/stdc++.h> using namespace std; const int maxn=100000+10; const int INF=2*int(1e9)+10; #define LL long long int cmd(int a,int b){ return a>b; } int main(){ int num[6]={1,2,4,7,15,34}; sort(num,num+6); //按从小到大排序 int pos1=lower_bound(num,num+6,7)-num; //返回数组中第一个大于或等于被查数的值 int pos2=upper_bound(num,num+6,7)-num; //返回数组中第一个大于被查数的值 cout<<pos1<<" "<<num[pos1]<<endl; cout<<pos2<<" "<<num[pos2]<<endl; sort(num,num+6,cmd); //按从大到小排序 int pos3=lower_bound(num,num+6,7,greater<int>())-num; //返回数组中第一个小于或等于被查数的值 int pos4=upper_bound(num,num+6,7,greater<int>())-num; //返回数组中第一个小于被查数的值 cout<<pos3<<" "<<num[pos3]<<endl; cout<<pos4<<" "<<num[pos4]<<endl; return 0; }

随机函数rand()

• rand()不需要参数，它会返回一个从0到最大随机数的任意整数，最大随机数的大小通常是固定的一个大整数。
• 如果你要产生0~99这100个整数中的一个随机整数，可以表达为：int num = rand() % 100;

STL数值算法

• 注意添加头文件——#include< numeric>

• 函数	说明
  accumulate(first,last, init)	元素累加
  inner_product(first, last, first2, init)	內积，将first1到last1之间的对象（左闭右开），与first2及其对应位置的对象相乘，并且加上init（相当于实数的点积）
  partial_sum(first, last, result)	局部总和。partial_sum() 会计算出输入序列中长度从1开始不断增加的序列的和，所以第一个输出值就是第一个元素，下一个值是前两个元素的和，再下一个值就是前三个元素的和，以此类推
  adjacent_difference(first, last, result)	相邻元素的差，右边减左边，第一个元素不变
  iota(begin,end,start)	用连续的 T 类型值填充序列。前两个参数是定义序列的正向迭代器，第三个参数是初始的 T 值。默认加1

• accumulate的例子

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

  #include <iostream> #include <vector> #include <algorithm> #include<numeric> using namespace std; int main() { vector<int> dp; for (int i = 1; i < 100; ++i) { dp.push_back(i); } int ret = accumulate(dp.begin(), dp.end(), 0); cout << ret << endl; return 0; } /*输出 4950 */

• inner_product(first, last, first2, init)的例子

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21

  #include <iostream> #include <vector> #include <algorithm> #include<numeric> using namespace std; int main() { vector<int> dp, dp1; for (int i = 1; i < 5; ++i) { dp.push_back(i); dp1.push_back(i + 1); } int ret = inner_product(dp.begin(), dp.end(), dp1.begin(), 0); cout << ret << endl; return 0; } /*输出 40=1*2+2*3+3*4+4*5 */

• partial_sum 和adjacent_difference的例子

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26

  #include <iostream> #include <vector> #include <algorithm> #include<iterator> #include<numeric> using namespace std; int main() { //源数据 std::vector<int> data{ 2, 3, 5, 7, 11, 13, 17, 19 }; std::cout << "Original data: "; std::copy(std::begin(data), std::end(data), std::ostream_iterator<int>{std::cout, " "}); //相邻差值，保存到原data里面 std::adjacent_difference(std::begin(data), std::end(data), std::begin(data)); std::cout << "\nDifferences : "; std::copy(std::begin(data), std::end(data), std::ostream_iterator<int>{std::cout, " "}); //局部总和，直接输出，也可以保存到新的vector里面 std::cout << "\nPartial sums : "; std::partial_sum(std::begin(data), std::end(data), std::ostream_iterator<int>{std::cout, " "}); std::cout << std::endl; return 0; }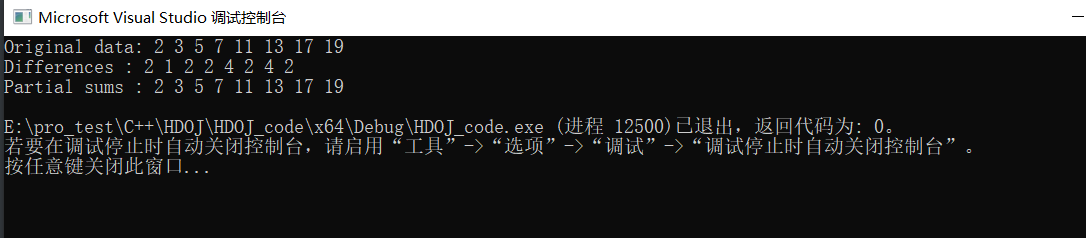

  

• 定义在 numeric 头文件中的 iota() 函数模板会用连续的 T 类型值填充序列。前两个参数是定义序列的正向迭代器，第三个参数是初始的 T 值。默认加1。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

  #include <iostream> #include <vector> #include <algorithm> #include <numeric> using namespace std; int main() { vector<int> dp; dp.resize(26); iota(dp.begin(),dp.end(),0); for(auto &i:dp){ cout<<i<<" "; } cout<<endl; return 0; }

  

求前缀和

• 使用函数 partial_sum 计算判断

• 

• 注意点

  • partial_sum(data.begin(),data.end(),partial.begin()); 如果partial没有开辟空间，使用begin会报错。
  • std::back_inserter 则不会报错，因为这样是从尾部插入，每次都开辟空间。

Lambda表达式

基本理论1

• 基本构成

  1 2 3 4 5 6

  [capture](parameters) mutable ->return-type { statement } [函数对象参数](操作符重载函数参数)mutable ->返回值{函数体} //mutable省略的话表示参数只是只读状态，除非传入引用

• ①函数对象参数；

  []，标识一个Lambda的开始，这部分必须存在，不能省略。函数对象参数是传递给编译器自动生成的函数对象类的构造函数的。函数对象参数只能使用那些到定义Lambda为止时Lambda所在作用范围内可见的局部变量（包括Lambda所在类的this）。函数对象参数有以下形式：

  • 空。没有使用任何函数对象参数。
  • =。函数体内可以使用Lambda所在作用范围内所有可见的局部变量（包括Lambda所在类的this），并且是值传递方式（相当于编译器自动为我们按值传递了所有局部变量）。
  • &。函数体内可以使用Lambda所在作用范围内所有可见的局部变量（包括Lambda所在类的this），并且是引用传递方式（相当于编译器自动为我们按引用传递了所有局部变量）
  • this。函数体内可以使用Lambda所在类中的成员变量。
  • a。将a按值进行传递。按值进行传递时，函数体内不能修改传递进来的a的拷贝，因为默认情况下函数是const的。要修改传递进来的a的拷贝，可以添加mutable修饰符。
  • &a。将a按引用进行传递。
  • a, &b。将a按值进行传递，b按引用进行传递。
  • =，&a, &b。除a和b按引用进行传递外，其他参数都按值进行传递。
  • &, a, b。除a和b按值进行传递外，其他参数都按引用进行传递。

• ② 操作符重载函数参数；

  标识重载的()操作符的参数，没有参数时，这部分可以省略。参数可以通过按值（如：(a,b)）和按引用（如：(&a,&b)）两种方式进行传递。

• ③ 可修改标示符；

  mutable声明，这部分可以省略。按值传递函数对象参数时，加上mutable修饰符后，可以修改按值传递进来的拷贝（注意是能修改拷贝，而不是值本身）。

• 1 2 3 4 5 6 7 8 9 10

  //例子 QPushButton * myBtn = new QPushButton (this); QPushButton * myBtn2 = new QPushButton (this); myBtn2->move(100,100); int m = 10; connect(myBtn,&QPushButton::clicked,this,[m] ()mutable { m = 100 + 10; qDebug() << m; }); connect(myBtn2,&QPushButton::clicked,this,[=] () { qDebug() << m; }); qDebug() << m;

• ④ 函数返回值；

  ->返回值类型，标识函数返回值的类型，当返回值为void，或者函数体中只有一处return的地方（此时编译器可以自动推断出返回值类型）时，这部分可以省略。

• ⑤ 是函数体；

  {}，标识函数的实现，这部分不能省略，但函数体可以为空。

• 建议一般用=，按值传递，外加mutable修饰符。

基本理论2

使用 STL 时，往往会大量用到函数对象，为此要编写很多函数对象类。有的函数对象类只用来定义了一个对象，而且这个对象也只使用了一次，编写这样的函数对象类就有点浪费。

而且，定义函数对象类的地方和使用函数对象的地方可能相隔较远，看到函数对象，想要查看其 operator() 成员函数到底是做什么的也会比较麻烦。

对于只使用一次的函数对象类，能否直接在使用它的地方定义呢？Lambda 表达式能够解决这个问题。使用 Lambda 表达式可以减少程序中函数对象类的数量，使得程序更加优雅。

Lambda 表达式的定义形式如下：

[外部变量访问方式说明符] (参数表) -> 返回值类型 { 语句块 }

其中，“外部变量访问方式说明符”可以是=或&，表示{}中用到的、定义在{}外面的变量在{}中是否允许被改变。=表示不允许，&表示允许。当然，在{}中也可以不使用定义在外面的变量。“-> 返回值类型”可以省略。

下面是一个合法的Lambda表达式：

[=] (int x, int y) -> bool {return x%10 < y%10; }

Lambda 表达式实际上是一个函数，只是它没有名字。下面的程序段使用了上面的 Lambda 表达式：

程序第 2 行使得数组 a 按个位数从小到大排序。具体的原理是：sort 在执行过程中，需要判断两个元素 x、y 的大小时，会以 x、y 作为参数，调用 Lambda 表达式所代表的函数，并根据返回值来判断 x、y 的大小。这样，就不用专门编写一个函数对象类了。

第 3 行，for_each 的第 3 个参数是一个 Lambda 表达式。for_each 执行过程中会依次以每个元素作为参数调用它，因此每个元素都被输出。

下面是用到了外部变量的Lambda表达式的程序：

第 8 行，[&]表示该 Lambda 表达式中用到的外部变量 total 是传引用的，其值可以在表达式执行过程中被改变（如果使用[=]，编译无法通过）。该 Lambda 表达式每次被 for_each 执行时，都将 a 中的一个元素累加到 total 上，然后将该元素加倍。

实际上，“外部变量访问方式说明符”还可以有更加复杂和灵活的用法。例如：

• [=, &x, &y]表示外部变量 x、y 的值可以被修改，其余外部变量不能被修改；
• [&, x, y]表示除 x、y 以外的外部变量，值都可以被修改。

前缀和

• 一种预处理手段

• 二、如何得到前缀和？

  一维前缀和：

  很容易就可以发现：

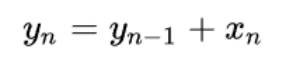
  代码实现如下：

  1 2 3 4 5

  for(int i=0;i<n;i++) { if(i==0) y[i]=x[i]; else y[i]=y[i-1]+x[i]; }

  二维前缀和：（面积）

  二维前缀和实际上就是一个矩阵内值的和，而矩阵又可以由两个行数或列数少一的子矩阵组合后，删去重合部分再加上右下角的值来构成，也就是以下式子：

  

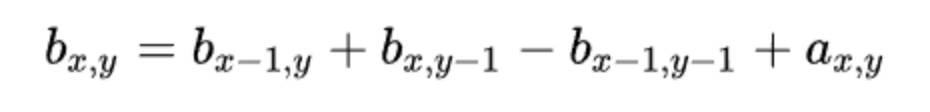
  代码实现如下：

  1 2 3 4 5 6 7 8

  for(int y=0;y<n;y++)//n行 for(int x=0;x<m;x++)//m列 { if(x==0&&y==0) b[y][x]=a[y][x];//左上角的值 else if(x==0) b[y][x]=b[y-1][x]+a[y][x];//第一列 else if(y==0) b[y][x]=b[y][x-1]+a[y][x];//第一行 else b[y][x]=b[y-1][x]+b[y][x-1]-b[y-1][x-1]+a[y][x];//递归 }

回溯算法（DFS:深度优先搜索）

• 回溯和递归的区别

  • 递归：为了描述问题的某一状态，必须用到该状态的上一状态，而描述上一状态，又必须用到上一状态的上一状态……这种用自已来定义自己的方法，称为递归定义。形式如 f(n) = n*f(n-1), if n=0,f(n)=1。
  • 回溯：从问题的某一种可能出发, 搜索从这种情况出发所能达到的所有可能, 当这一条路走到” 尽头 “的时候, 再倒回出发点, 从另一个可能出发, 继续搜索. 这种不断” 回溯 “寻找解的方法, 称作” 回溯法 “。
  • 递归是一种算法结构，递归会出现在子程序中自己调用自己或间接地自己调用自己。最直接的递归应用就是计算连续数的阶乘，计算规律：n!=(n-1)!*n。
  • 回溯是一种算法思想，可以用递归实现。通俗点讲回溯就是一种试探，类似于穷举，但回溯有“剪枝”功能，比如求和问题。给定7个数字，1 2 3 4 5 6 7求和等于7的组合，从小到大搜索，选择1+2+3+4 =10>7，已经超过了7，之后的5 6 7就没必要在继续了，这就是一种搜索过程的优化。

• 回溯法，一般可以解决如下几种问题：

  • 组合问题：N个数里面按一定规则找出k个数的集合
  • 排列问题：N个数按一定规则全排列，有几种排列方式
  • 切割问题：一个字符串按一定规则有几种切割方式
  • 子集问题：一个N个数的集合里有多少符合条件的子集
  • 棋盘问题：N皇后，解数独等等

• 代码模板（重要）

  1 2 3 4 5 6 7 8 9 10 11 12 13

  //一般无返回值，backtracking函数纵向搜索，for循环横向搜索。 void backtracking(路径，选择列表) { if (终止条件) { 存放结果; return; } for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) { 处理节点; backtracking(路径，选择列表); // 递归 回溯，撤销处理结果 } }

组合问题

• 77 组合问题

• 给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

  你可以按 任何顺序 返回答案。

  • 思路：回溯递归

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26

  class Solution { public: vector<vector<int>> ret;//返回值 vector<int> path;//暂缓的路径 void trackbacking(int n,int k,int start){ //回溯结束条件 if(path.size()==k){ ret.push_back(path); return; } //树的横向搜索 for(int i=start;i<=n;++i){ path.push_back(i);//处理该节点 trackbacking(n, k, i+1);//递归，树的纵向搜索 path.pop_back();//回溯 } } vector<vector<int>> combine(int n, int k) { ret.clear(); path.clear(); trackbacking(n, k,1); return ret; } };

• 剪枝的优化

  • 可以剪枝的地方就在递归中每一层的for循环所选择的起始位置。

    如果for循环选择的起始位置之后的元素个数 已经不足 我们需要的元素个数了，那么就没有必要搜索了。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26

  class Solution { public: vector<vector<int>> ret;//返回值 vector<int> path;//暂缓的路径 void trackbacking(int n,int k,int start){ //回溯结束条件 if(path.size()==k){ ret.push_back(path); return; } //树的横向搜索 for(int i=start;i<=n-(k-path.size())+1;++i){//优化地方，剪枝在for循环 path.push_back(i);//处理该节点 trackbacking(n, k, i+1);//递归，树的纵向搜索 path.pop_back();//回溯 } } vector<vector<int>> combine(int n, int k) { ret.clear(); path.clear(); trackbacking(n, k,1); return ret; } };

• 216. 组合总和 III

  找出所有相加之和为 n的 k 个数的组合。组合中只允许含有 1 - 9 的正整数，并且每种组合中不存在重复的数字。

  说明：

  • 所有数字都是正整数。

  • 解集不能包含重复的组合。

  • 思路，加多一个限制条件，递归回溯

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32

  class Solution { public: vector<int> path; vector<vector<int>> ret; void backtracking(int k,int n,int start,int &sum1){ //返回条件 if(sum1==n && path.size()==k){ ret.push_back(path); return; } for(int i=start;i<=9;++i){ //处理节点 path.push_back(i); sum1+=i; //递归 backtracking(k, n, i+1, sum1);//i+1所以不重复 //回溯 path.pop_back(); sum1-=i; } } vector<vector<int>> combinationSum3(int k, int n) { int sum=0; ret.clear(); path.clear(); backtracking(k, n, 1, sum); return ret; } };

  • 剪枝，在递归的时候剪枝，在for循环的时候剪枝

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37

  class Solution { public: vector<int> path; vector<vector<int>> ret; void backtracking(int k,int n,int start,int &sum1){ //剪枝 if(sum1>n){ return; } //返回条件 if(sum1==n && path.size()==k){ ret.push_back(path); return; } for(int i=start;i<= 9-(k-path.size())+1;++i)//剪枝优化 { //处理节点 path.push_back(i); sum1+=i; //递归 backtracking(k, n, i+1, sum1); //回溯 path.pop_back(); sum1-=i; } } vector<vector<int>> combinationSum3(int k, int n) { int sum=0; ret.clear(); path.clear(); backtracking(k, n, 1, sum); return ret; } };

• 22. 括号生成

  数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41

  class Solution { public: string path; vector<string> ret; void backtracking(int n, int &use_left, int &use_right){ //注意返回条件，不然会死循环 if(use_left<use_right){ return; } if(use_left>n||use_right>n){ return; } if(use_left==n&&use_right==n){ ret.push_back(path); return; } //左括号 path.push_back('('); ++use_left; backtracking(n,use_left, use_right); --use_left; path.pop_back(); //右括号 path.push_back(')'); ++use_right; backtracking(n, use_left, use_right); --use_right; path.pop_back(); } vector<string> generateParenthesis(int n) { int left=0,right=0; ret.clear(); path.clear(); backtracking(n, left, right); return ret; } };

• 79. 单词搜索

  给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

  单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58

  class Solution { public: const vector<int> dx{-1,1,0,0}; const vector<int> dy{0,0,1,-1}; bool backtracking(string word, vector<vector<char>>& board, vector<vector<bool>>& used, int row, int col, int rows, int cols ,int nums){ //直接判断每一个字符，不要合并完全再判断是否相等 if(board[row][col]!=word[nums]){ return false; } if(nums==word.size()-1){ return true; } used[row][col]=true; ++nums; bool flag=false; for(int i=0;i<4;++i){ int newrow=row+dx[i]; int newcol=col+dy[i]; if(newrow>=0&&newcol>=0&&newrow<rows&&newcol<cols){ if(used[newrow][newcol]){ continue;//保持不变，仍是false } else{ flag=flag||backtracking(word, board, used, newrow, newcol, rows, cols,nums); } } } used[row][col]=false; --nums; return flag; } bool exist(vector<vector<char>>& board, string word) { int rows=board.size(); int cols=board[0].size(); bool check=false; vector<vector<bool>> used(rows,vector<bool>(cols,false)); for(int i=0;i<rows;++i){ for(int j=0;j<cols;++j){ if(board[i][j]==word[0]){ //第一个 used[i][j]=true; check=backtracking(word, board, used, i, j, rows, cols,0); if(check){ return true; } used[i][j]=false; } } } return check; } };

• 17. 电话号码的字母组合

  给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。

  • 思路：回溯递归，不过先创建一个映射
  • 注意回溯要所有的因素都回溯完

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40

  class Solution { public: //定义映射 const string letter_map[10]={ "","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz" }; string path; vector<string> ret; void backtracking(int n, string &digits,int start){ if(path.size()==n){ ret.push_back(path); return; } if(start>=n){ return; } char temp=digits[start]; string temp1=letter_map[temp-'0']; for(int i=0;i<temp1.size();++i){ path.push_back(temp1[i]);//处理节点 backtracking(n ,digits,++start);//递归 path.pop_back();//回溯 --start; } } vector<string> letterCombinations(string digits) { int n=digits.size(); path.clear(); ret.clear(); if(n==0){ return ret; } backtracking(n,digits,0); return ret; } };

• 39 组合总和

  • 题干：给定一个无重复元素的正整数数组 candidates 和一个正整数 target ，找出 candidates 中所有可以使数字和为目标数 target 的唯一组合。

    candidates 中的数字可以无限制重复被选取。如果至少一个所选数字数量不同，则两种组合是唯一的。

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36

  class Solution { public: vector<vector<int>> ret; vector<int> path; void backtracking(int target, int start, int sum, vector<int>& candidates){ //结束条件 if(sum>target){ return; } if(sum==target){ ret.push_back(path); return; } for(int i=start;i<candidates.size();++i){ sum+=candidates[i]; path.push_back(candidates[i]); //递归 backtracking(target, i, sum, candidates);//可重复选取 //回溯 sum-=candidates[i]; path.pop_back(); } } vector<vector<int>> combinationSum(vector<int>& candidates, int target) { path.clear(); ret.clear(); if(candidates.size()==0){ return ret; } backtracking(target, 0, 0, candidates); return ret; } };

• 40. 组合总和 II

  给定一个数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

  candidates 中的每个数字在每个组合中只能使用一次。

  **注意：**解集不能包含重复的组合。

• 难点在于如何去重复——从小到大排序之后进行前后比较，比较重复的则跳到下一个循环，减少横向遍历，即去重。因为数组candidates可能有重复的元素。

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47

  class Solution { public: vector<vector<int>> ret; vector<int> path; void backtracking(int target,int start,int n,int sum,vector<int>& candidates){ if(sum==target){ //判断重复_这样会超时 // for(auto &i:ret){ // if(i==path){ // return; // } // } ret.push_back(path); return; } if(start>=n){ return; } if(sum>target){ return; } for(int i=start;i<n;++i){ //去重操作，因为已经排序好了，所以for循环的横向遍历不能重复遍历相同的元素 //注意一定是i>start，保证第一个是可以的，第二个不行 if(i>start && candidates[i]==candidates[i-1]){ continue;; } path.push_back(candidates[i]); sum+=candidates[i]; backtracking(target, i+1, n, sum, candidates); //回溯 path.pop_back(); sum-=candidates[i]; } } vector<vector<int>> combinationSum2(vector<int>& candidates, int target) { int n=candidates.size(); int sum=0; path.clear(); ret.clear(); sort(candidates.begin(),candidates.end()); backtracking(target,0,n,sum,candidates); return ret; } };

分割问题

• 131. 分割回文串

  给你一个字符串 s，请你将 s 分割成一些子串，使每个子串都是 回文串 。返回 s 所有可能的分割方案。

  回文串 是正着读和反着读都一样的字符串。

  • 思路
  • 

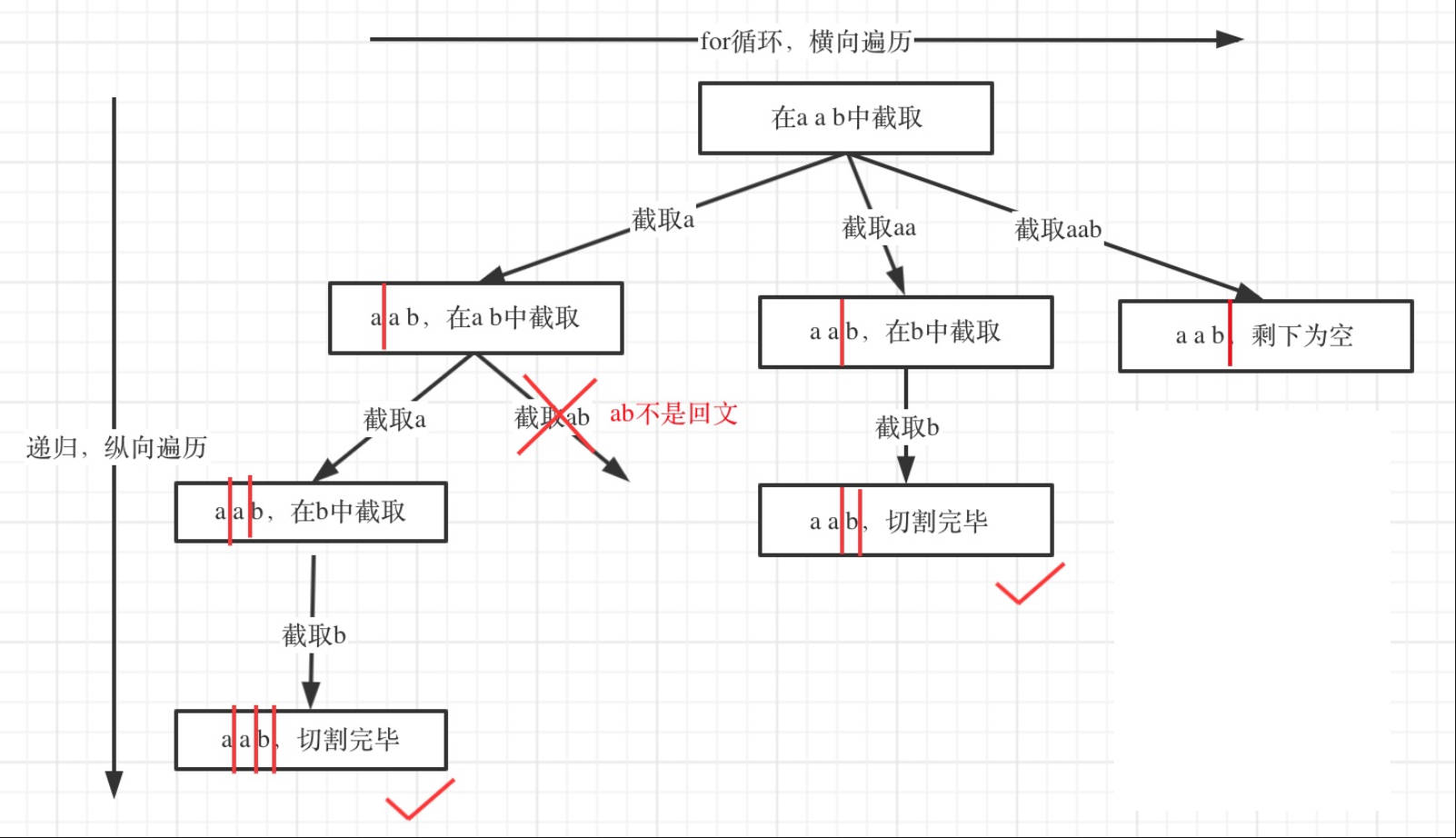
  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49

  class Solution { public: bool check(string & a){ int n=a.size(); if(n==1){ return true; } for(int i=0,j=n-1;i<j;++i,--j){ if(a[i]!=a[j]){ return false; } } return true; } vector<vector<string>> ret; vector<string> path; void backtracking(string &s,int start){ //如果起始位置大于n，说明已经切割完了 if(start>=s.size()){ ret.push_back(path); return; } for(int i=start;i<s.size();++i){ //获取s的子串 string str=s.substr(start,i-start+1);//开始位置+长度 if(check(str)){ path.push_back(str); }else{ continue; } //纵向递归 backtracking(s, i+1); //回溯 path.pop_back(); } } vector<vector<string>> partition(string s) { ret.clear(); path.clear(); if(s.size()==0){ return ret; } backtracking(s, 0); return ret; } };

• 93. 复原 IP 地址

  有效 IP 地址 正好由四个整数（每个整数位于 0 到 255 之间组成，且不能含有前导 0），整数之间用 '.' 分隔。

  • 例如："0.1.2.201" 和 "192.168.1.1" 是 有效 IP 地址，但是 "0.011.255.245"、"192.168.1.312" 和 "192.168@1.1" 是 无效 IP 地址。

  给定一个只包含数字的字符串 s ，用以表示一个 IP 地址，返回所有可能的有效 IP 地址，这些地址可以通过在 s 中插入 '.' 来形成。你不能重新排序或删除 s 中的任何数字。你可以按 任何 顺序返回答案。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61

  class Solution { public: //最终返回的数组 vector<string> ret; //判断s的[start,end]是否合格 bool check(string &s, int start, int end){ if(start>end){ return false; } //开头为0无效 if(s[start]=='0' && start!=end){ return false; } int num=0; //因为只包含数字，不用考虑其他的无效字符 for(int i=start;i<=end;++i){ num=10*num+(s[i]-'0'); if(num>255){ return false; } } return true; } //pointNum是逗号个数， void backtracking(string &s, int start,int pointNum){ if(pointNum==3){ if(check(s,start,s.size()-1)){ ret.push_back(s); return; } return; } for(int i=start;i<s.size();++i){ if(check(s, start, i)){ //操作节点 s.insert(s.begin()+i+1, '.'); ++pointNum; //纵向递归,插入了一个‘.’，所以 +2 backtracking(s, i+2, pointNum); //回溯 s.erase(s.begin()+i+1);//在哪里插入，就在哪里删除 --pointNum; } } } vector<string> restoreIpAddresses(string s) { int n=s.size(); ret.clear(); if(n==0||n>12){ return ret; } backtracking(s, 0, 0); return ret; } };

子集问题

• 要清楚子集问题和组合问题、分割问题的的区别：

  • 子集是收集树形结构中树的所有节点的结果。
  • 组合问题、分割问题是收集树形结构中叶子节点的结果。

• 78. 子集

  给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。

  解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33

  class Solution { public: vector<vector<int>> ret; vector<int> path; void backtracking(vector<int>& nums, int start){ if(start>=nums.size()){ return; } for(int i=start;i<nums.size();++i){ path.push_back(nums[i]); ret.push_back(path); //递归 backtracking(nums, i+1); //回溯 path.pop_back(); } } vector<vector<int>> subsets(vector<int>& nums) { int n=nums.size(); path.clear(); ret.clear(); ret.push_back(path);//插入空集 if(n==0){ return ret; } backtracking(nums, 0); return ret; } };

• 90. 子集 II

  给你一个整数数组 nums ，其中可能包含重复元素，请你返回该数组所有可能的子集（幂集）。

  解集 不能 包含重复的子集。返回的解集中，子集可以按 任意顺序 排列。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37

  class Solution { public: vector<vector<int>> ret; vector<int> path; void backtracking(vector<int>& nums, int start){ if(start>=nums.size()){ return; } for(int i=start;i<nums.size();++i){ //注意一定是i>start ,而不是i>0，此处是防止重复 if(i>start && nums[i]==nums[i-1]){ continue; } path.push_back(nums[i]); ret.push_back(path); //递归 backtracking(nums, i+1); //回溯 path.pop_back(); } } vector<vector<int>> subsetsWithDup(vector<int>& nums) { //先排序 int n=nums.size(); sort(nums.begin(),nums.end()); ret.clear(); path.clear(); ret.push_back(path); if(n==0){ return ret; } backtracking(nums, 0); return ret; } };

排列问题

• 46. 全排列

  给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

  • 思路——设置一个哈希表或者数组判断哪个下标已经读过，不在读取即可

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46

  class Solution { public: vector<int> path; vector<vector<int>> ret; unordered_set<int> dp; // vector<bool> pred; void backtracking(vector<int>& nums){ if(path.size()==nums.size()){ ret.push_back(path); return; } for(int i=0;i<nums.size();++i){ if(dp.count(i)){ continue; } // if(pred[i]==true){ // continue; // } // pred[i]=true; dp.insert(i); path.push_back(nums[i]); //递归 backtracking(nums); //回溯 // pred[i]=false; dp.erase(i); path.pop_back(); } } vector<vector<int>> permute(vector<int>& nums) { int n=nums.size(); // pred.clear(); // pred.resize(n,false); ret.clear(); path.clear(); dp.clear(); if(n==0){ return ret; } backtracking(nums); return ret; } };

• 47. 全排列 II

  给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

  • 就是去重比较麻烦，思路就是同一层次的相同值不在进行递归

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47

  class Solution { public: vector<int> path; vector<vector<int>> ret; void backtracking(vector<int>& nums, vector<bool>& check){ if(path.size()==nums.size()){ ret.push_back(path); return; } for(int i=0;i<nums.size();++i){ if(i>0 &&nums[i]==nums[i-1] && check[i-1]==false){ continue;//证明同一层的前一个已经遍历过了。 } if(check[i]==true)//保证其他元素不遍历多次 { continue; } check[i]=true; path.push_back(nums[i]); //递归 backtracking(nums, check); //回溯 check[i]=false; path.pop_back(); } } vector<vector<int>> permuteUnique(vector<int>& nums) { int n=nums.size(); sort(nums.begin(),nums.end());//注意一定要先排序 ret.clear(); path.clear(); vector<bool> check(n,false); if(n==0){ return ret; } backtracking(nums, check); return ret; } };

N皇后

• 51. N 皇后

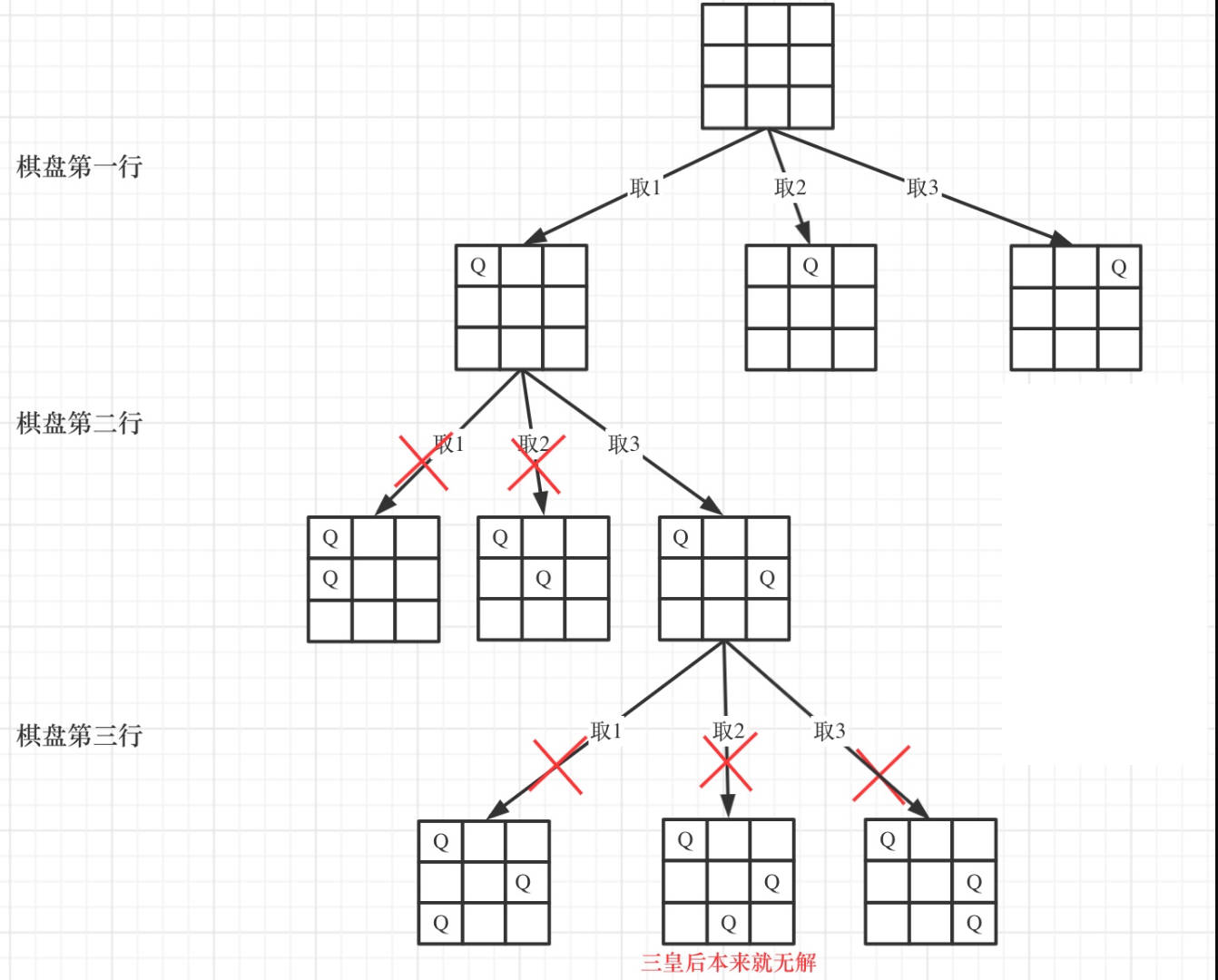
  n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

  给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

  每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

  首先来看一下皇后们的约束条件：

  1. 不能同行
  2. 不能同列
  3. 不能同斜线（45,135）

• 

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71

  class Solution { public: vector<vector<string>> ret; //因为要直接检验是否合格，所以要输入引用,且初始化均为'.' void backtracking(int n, int row, vector<string> &path){ if(row>=n){ ret.push_back(path); return; } //横向遍历 for(int col=0;col<n;++col){ //判断合格就可以放q if(isValid(n,row,col,path)){ path[row][col]='Q'; backtracking(n, row+1, path); //回溯 path[row][col]='.'; } } } bool isValid(int n, int row, int col, vector<string> &path){ //因为横向遍历已经检验了水平的合格问题，只需要检验竖直、45、135三个方向 //检验竖直 for(int i=0;i<n;++i){ if(i==row){ continue; } if(path[i][col]=='Q'){ return false; break; } } //检验45 for(int i=row-1,j=col-1;i>=0&&j>=0;--i,--j){ if(path[i][j]=='Q'){ return false; } } for(int i=row+1,j=col+1;i<n&&j<n;++i,++j){ if(path[i][j]=='Q'){ return false; } } //检验135 for(int i=row-1,j=col+1;i>=0&&j<n;--i,++j){ if(path[i][j]=='Q'){ return false; } } for(int i=row+1,j=col-1;i<n&&j>=0;++i,--j){ if(path[i][j]=='Q'){ return false; } } return true; } vector<vector<string>> solveNQueens(int n) { ret.clear(); string str(n,'.'); vector<string> path(n,str); backtracking(n, 0, path); return ret; } };

解数独

• 37. 解数独

  编写一个程序，通过填充空格来解决数独问题。

  数独的解法需 遵循如下规则：

  1. 数字 1-9 在每一行只能出现一次。
  2. 数字 1-9 在每一列只能出现一次。
  3. 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。（请参考示例图）

  数独部分空格内已填入了数字，空白格用 '.' 表示。

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64

  class Solution { public: bool backtracking(vector<vector<char>> &board){ for(int i=0;i<board.size();++i){ for(int j=0;j<board[0].size();++j){ if(board[i][j]!='.'){ continue; } for(char k='1';k<='9';++k){ //先判断是否可以 if(isValid(i,j,k,board)){ board[i][j]=k; if(backtracking(board)) return true;//纵向递归,返回确认 board[i][j]='.';//回溯 } } //9个数字都不行，返回失败 return false; } } //所有81遍历完，没问题，返回 return true; } bool isValid(int i, int j, char k, vector<vector<char>> &board){ //判断横 for(int col=0;col<board[0].size();++col){ if(col==j){ continue; } if(board[i][col]==k){ return false; } } //判断竖 for(int row=0;row<board.size();++row){ if(row==i){ continue; } if(board[row][j]==k){ return false; } } //判断9宫格 int row_9=i/3; int col_9=j/3; for(int row=3*row_9;row<3*(row_9+1);++row){ for(int col=3*col_9;col<3*(col_9+1);++col){ if(col==j &&row==i){ continue; } if(board[row][col]==k){ return false; } } } return true; } void solveSudoku(vector<vector<char>>& board) { backtracking(board); } };

经典dfs题目

• 254. 因子的组合

  整数可以被看作是其因子的乘积。

  例如：

  8 = 2 x 2 x 2;
    = 2 x 4.
  

  请实现一个函数，该函数接收一个整数 n 并返回该整数所有的因子组合。

  注意：

  1. 你可以假定 n 为永远为正数。
  2. 因子必须大于 1 并且小于 n。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

  class Solution { public: vector<vector<int>> dfs(int n, int start){ vector<vector<int>> ret; //for循环已经蕴含结束递归的条件了 for(int i=start;i*i<=n;++i){ if(n%i==0){ ret.push_back({i,n/i});//先加进来，i<根号n，保证没有重复 //从i开始，保证26 223，而不会有232 for(auto v:dfs(n/i, i)){ v.push_back(i);//加回之前的i ret.push_back(v); } } } return ret; } vector<vector<int>> getFactors(int n) { vector<vector<int>> result; result=dfs(n, 2); return result; } };

• 329. 矩阵中的最长递增路径

  给定一个 m x n 整数矩阵 matrix ，找出其中 最长递增路径 的长度。

  对于每个单元格，你可以往上，下，左，右四个方向移动。 你 不能 在 对角线 方向上移动或移动到 边界外（即不允许环绕）。

  • 思路：使用一个dp数组记录，记忆化dfs——记住以下这种写法

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34

  class Solution { public: const vector<vector<int>> direct={{-1,0},{1,0},{0,-1},{0,1}};//四个方向 int dfs(vector<vector<int>>& matrix, int row, int col, vector<vector<int>>& check){ if(check[row][col]!=0){ return check[row][col]; } check[row][col]=1;//初始化为0方便判断，所以现在更改为1 for(int i=0;i<4;++i){ int newrow=row+direct[i][0]; int newcol=col+direct[i][1]; if(newrow>=0 && newrow<matrix.size() && newcol>=0 &&newcol<matrix[0].size() && matrix[row][col]<matrix[newrow][newcol]){ check[row][col]=max(check[row][col], dfs(matrix,newrow, newcol,check)+1); } } return check[row][col]; } int longestIncreasingPath(vector<vector<int>>& matrix) { int n=matrix.size(); int m=matrix[0].size(); vector<vector<int>> check(n,vector<int>(m,0)); int len=1; for(int i=0;i<n;++i){ for(int j=0;j<m;++j){ len=max(len,dfs(matrix, i, j, check)); } } return len; } };

• 576. 出界的路径数

  给你一个大小为 m x n 的网格和一个球。球的起始坐标为 [startRow, startColumn] 。你可以将球移到在四个方向上相邻的单元格内（可以穿过网格边界到达网格之外）。你 最多 可以移动 maxMove 次球。

  给你五个整数 m、n、maxMove、startRow 以及 startColumn ，找出并返回可以将球移出边界的路径数量。因为答案可能非常大，返回对 109 + 7 取余 后的结果。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47

  //思路：dfs深度优先搜索，不过记忆化搜索，不然会超时 class Solution { public: const vector<vector<int>> dir={{-1,0},{1,0},{0,-1},{0,1}}; const int MOD=1000000007; //m行n列 ，i为行数，j为列数;dp[i][j][n] int dfs(int m,int n, int mov, int i, int j, vector<vector<vector<int>>> &dp){ if(i<0||j<0||i>=m||j>=n){ return 1; } //没有移动次数了 if(mov==0){ return 0; } //如果已经存在记忆化搜索,一般不会搜索到[i][j][0]，因为恒等于-1，且上条已经返回了 if(dp[i][j][mov]!=-1){ return dp[i][j][mov]; } //剪枝，怎么走都不会出界 if(i-mov>=0 &&j-mov>=0 &&i+mov<m && j+mov<n){ dp[i][j][mov]=0; return 0; } //深度优先搜索,可以走回起点，反正也会被剪枝 int sum=0; for(int p=0;p<4;++p){ int newrow=i+dir[p][0]; int newcol=j+dir[p][1]; sum=(sum+dfs(m,n,mov-1,newrow,newcol,dp))%MOD;//记得取余 } dp[i][j][mov]=sum; return sum; } int findPaths(int m, int n, int maxMove, int startRow, int startColumn) { //三维数组的初始化 vector<vector<vector<int>>> dp(m,vector<vector<int>>(n,vector<int>(maxMove+1,-1))); int ret=dfs(m,n,maxMove,startRow,startColumn,dp); return ret; } };

• 733. 图像渲染

  有一幅以二维整数数组表示的图画，每一个整数表示该图画的像素值大小，数值在 0 到 65535 之间。

  给你一个坐标 (sr, sc) 表示图像渲染开始的像素值（行 ，列）和一个新的颜色值 newColor，让你重新上色这幅图像。

  为了完成上色工作，从初始坐标开始，记录初始坐标的上下左右四个方向上像素值与初始坐标相同的相连像素点，接着再记录这四个方向上符合条件的像素点与他们对应四个方向上像素值与初始坐标相同的相连像素点，……，重复该过程。将所有有记录的像素点的颜色值改为新的颜色值。

  最后返回经过上色渲染后的图像。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54

  class Solution { public: //image_flag不是必须的，因为本来就更改了，天然防重特性 //可以使用减少代码量 /* const int dx[4] = {1, 0, 0, -1}; const int dy[4] = {0, 1, -1, 0}; void dfs(vector<vector<int>>& image, int x, int y, int color, int newColor) { if (image[x][y] == color) { image[x][y] = newColor; for (int i = 0; i < 4; i++) { int mx = x + dx[i], my = y + dy[i]; if (mx >= 0 && mx < image.size() && my >= 0 && my < image[0].size()) { dfs(image, mx, my, color, newColor); } } } } */ void pain(vector<vector<int>>& image,vector<vector<bool>>& image_flag, int sr, int sc, int newColor,int srcColor){ if(image_flag[sr][sc]){ return; } if(image[sr][sc]==srcColor){ image_flag[sr][sc]=true; image[sr][sc]=newColor; if(sr-1>=0){ pain(image,image_flag, sr-1, sc,newColor,srcColor); } if(sr+1<image.size()){ pain(image,image_flag, sr+1, sc,newColor,srcColor); } if(sc-1>=0){ pain(image,image_flag, sr, sc-1,newColor,srcColor); } if(sc+1<image[0].size()){ pain(image,image_flag, sr, sc+1,newColor,srcColor); } } } vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int newColor) { int row=image.size(); int col=image[0].size(); vector<vector<bool>> image_flag(row,vector<bool>(col,false)); int srcCol=image[sr][sc]; pain(image, image_flag, sr, sc, newColor, srcCol); return image; } };

• 695. 岛屿的最大面积

  给你一个大小为 m x n 的二进制矩阵 grid 。

  岛屿 是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0（代表水）包围着。

  岛屿的面积是岛上值为 1 的单元格的数目。

  计算并返回 grid 中最大的岛屿面积。如果没有岛屿，则返回面积为 0 。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34

  //思路：深度优先搜索即可，注意读取之后1变为0避免重复。 class Solution { public: const vector<int> dx{0,0,1,-1}; const vector<int> dy{1,-1,0,0}; int dfs(vector<vector<int>>& grid,int row,int col){ int ret=0; if(grid[row][col]){ grid[row][col]=0; ++ret; for(int i=0;i<4;++i){ int newrow=row+dy[i]; int newcol=col+dx[i]; if(newrow>=0&&newrow<grid.size()&&newcol>=0&&newcol<grid[0].size()){ ret+=dfs(grid, newrow, newcol); } } } return ret; } int maxAreaOfIsland(vector<vector<int>>& grid) { int ret=0; for(int i=0;i<grid.size();++i){ for(int j=0;j<grid[0].size();++j){ if(grid[i][j]){ ret=max(ret,dfs(grid, i, j)); } } } return ret; } };

• 200. 岛屿数量

  给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。

  岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

  此外，你可以假设该网格的四条边均被水包围。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33

  class Solution { public: const vector<int> dx{0,0,1,-1}; const vector<int> dy{1,-1,0,0}; void dfs(vector<vector<char>>& grid,int row,int col){ if(grid[row][col]=='1'){ grid[row][col]='0'; for(int i=0;i<4;++i){ int newrow=row+dx[i]; int newcol=col+dy[i]; if(newrow>=0&&newcol>=0&&newrow<grid.size()&&newcol<grid[0].size()){ dfs(grid, newrow, newcol); } } } } int numIslands(vector<vector<char>>& grid) { int rows=grid.size(); int cols=grid[0].size(); int ret=0; for(int i=0;i<rows;++i){ for(int j=0;j<cols;++j){ if(grid[i][j]=='1'){ ++ret; dfs(grid, i, j); } } } return ret; } };

• 130. 被围绕的区域

  给你一个 m x n 的矩阵 board ，由若干字符 'X' 和 'O' ，找到所有被 'X' 围绕的区域，并将这些区域里所有的 'O' 用 'X' 填充。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75

  class Solution { public: const vector<int> dx{0,0,1,-1}; const vector<int > dy{1,-1,0,0}; void dfs_dummy(vector<vector<char>>& board, int row, int col, int rows, int cols){ if(board[row][col]=='O'){ //寻找dummy哑结点，最后再回复 board[row][col]='#'; for(int i=0;i<4;++i){ int newrow=row+dx[i]; int newcol=col+dy[i]; if(newrow>=0&&newrow<rows&&newcol>=0&&newcol<cols){ dfs_dummy(board, newrow, newcol, rows, cols); } } } } void dfs(vector<vector<char>>& board, int row, int col, int rows, int cols){ if(board[row][col]=='O'){ board[row][col]='X'; for(int i=0;i<4;++i){ int newrow=row+dx[i]; int newcol=col+dy[i]; if(newrow>=1&&newrow<rows-1&&newcol>=1&&newcol<cols-1){ dfs(board, newrow, newcol, rows, cols); } } } } void solve(vector<vector<char>>& board) { int rows=board.size(); int cols=board[0].size(); if(rows<=2||cols<=2){ return; } //更改哑结点及其连通域 for(int i=0;i<cols;++i){ if(board[0][i]=='O'){ dfs_dummy(board, 0, i, rows, cols); } if(board[rows-1][i]=='O'){ dfs_dummy(board, rows-1, i, rows, cols); } } for(int i=0;i<rows;++i){ if(board[i][0]=='O'){ dfs_dummy(board, i, 0, rows, cols); } if(board[i][cols-1]=='O'){ dfs_dummy(board, i,cols-1, rows, cols); } } //深度优先搜索 for(int i=1;i<rows-1;++i){ for(int j=1;j<cols-1;++j){ if(board[i][j]=='O'){ dfs(board, i, j, rows, cols); } } } //恢复哑结点 for(int i=0;i<rows;++i){ for(int j=0;j<cols;++j){ if(board[i][j]=='#'){ board[i][j]='O'; } } } } };

• 582. 杀掉进程

  系统中存在 n 个进程，形成一个有根树结构。给你两个整数数组 pid 和 ppid ，其中 pid[i] 是第 i 个进程的 ID ，ppid[i] 是第 i 个进程的父进程 ID 。

  每一个进程只有 一个父进程 ，但是可能会有 一个或者多个子进程 。只有一个进程的 ppid[i] = 0 ，意味着这个进程 没有父进程 。

  当一个进程 被杀掉 的时候，它所有的子进程和后代进程都要被杀掉。

  给你一个整数 kill 表示要杀掉进程的 ID ，返回杀掉该进程后的所有进程 ID 的列表。可以按 任意顺序 返回答案。

  • 深度优先和广度优先都可以。

  • 广度优先

    1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

    class Solution { public: vector<int> killProcess(vector<int>& pid, vector<int>& ppid, int kill) { //建立哈希表,键是id号，值是以这个id为父亲的子进程的序号 unordered_map<int,vector<int>> check; for(int i=0;i<ppid.size();++i){ check[ppid[i]].push_back(i); } vector<int> ret; queue<int> dp; dp.push(kill); //层序遍历，因为一个进程可能有多个子进程 while(!dp.empty()){ int par=dp.front(); ret.push_back(par); dp.pop(); auto temp=check[par]; for(auto &i:temp){ dp.push(pid[i]); } } return ret; } };

  • 深度优先

    1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

    class Solution { public: vector<int> ret; void backtracking(unordered_map<int,vector<int>> &check, vector<int>& pid,int parent){ ret.push_back(parent); if(check.count(parent)){ auto i=check[parent]; for(auto &j:i){ backtracking(check, pid,pid[j]); } } } vector<int> killProcess(vector<int>& pid, vector<int>& ppid, int kill) { //建立哈希表,键是id号，值是以这个id为父亲的子进程的序号 unordered_map<int,vector<int>> check; for(int i=0;i<ppid.size();++i){ check[ppid[i]].push_back(i); } ret.clear(); backtracking(check, pid, kill); return ret; } };

栈递归

• 726. 原子的数量

  给你一个字符串化学式 formula ，返回 每种原子的数量 。

  原子总是以一个大写字母开始，接着跟随 0 个或任意个小写字母，表示原子的名字。

  如果数量大于 1，原子后会跟着数字表示原子的数量。如果数量等于 1 则不会跟数字。

  • 例如，"H2O" 和 "H2O2" 是可行的，但 "H1O2" 这个表达是不可行的。

  两个化学式连在一起可以构成新的化学式。

  • 例如 "H2O2He3Mg4" 也是化学式。

  由括号括起的化学式并佐以数字（可选择性添加）也是化学式。

  • 例如 "(H2O2)" 和 "(H2O2)3" 是化学式。

  返回所有原子的数量，格式为：第一个（按字典序）原子的名字，跟着它的数量（如果数量大于 1），然后是第二个原子的名字（按字典序），跟着它的数量（如果数量大于 1），以此类推。

• 思路：使用栈和哈希表；栈里面的元素是哈希表，哈希表存储原子名称及其个数

  • 如果是左括号，将一个空的哈希表压入栈中，进入下一层。
  • 如果不是括号，则读取一个原子名称，若后面还有数字，则读取一个数字，否则将该原子后面的数字视作 1。然后将原子及数字加入栈顶的哈希表中。
  • 如果是右括号，则说明遍历完了当前层，若括号右侧还有数字，则读取该数字num，否则将该数字视作 1。然后将栈顶的哈希表弹出，将弹出的哈希表中的原子数量与 num 相乘，加到上一层的原子数量中。
  • 遍历结束后，栈顶的哈希表即为化学式中的原子及其个数。遍历哈希表，取出所有「原子-个数」对加入数组中，对数组按照原子字典序排序，然后遍历数组，按题目要求拼接成答案。

• 重点是程序如何实现。

• c++有内置函数判断大小写和数字

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106

  class Solution { public: bool chcek_math(char src){ if(src>='0' &&src<='9'){ return true; } return false; } bool chcekSmall(char src){ if(src>='a' &&src<='z'){ return true; } return false; } bool chcekBig(char src){ if(src>='A'&&src<='Z'){ return true; } return false; } string countOfAtoms(string formula) { int n = formula.size(); stack<unordered_map<string,int>> record;//每一层括号都是哈希 vector<string> ret; int i =0; record.push({});//首先加入空的哈希，表示最后的结果 //判读数字和字母的匿名函数 auto parseAtom = [&]() -> string { string atom; atom += formula[i++]; // 扫描首字母 while (i < n && islower(formula[i])) { atom += formula[i]; // 扫描首字母后的小写字母 ++i; } return atom; }; auto parseNum = [&]() -> int { if (i == n || !isdigit(formula[i])) { return 1; // 不是数字，视作 1 } int num = 0; while (i < n && isdigit(formula[i])) { num = num * 10 + int(formula[i] - '0'); // 扫描数字 ++i; } return num; }; while(i<n){ char curr = formula[i]; if(curr =='('){ record.push({});//首先加入空的哈希，表示最后的结果 ++i; } else if(curr ==')'){ ++i; //计算数字 int num =0; if (i == n || !chcek_math(formula[i])) { num =1; }else{ while(i<n && chcek_math(formula[i])){ num=num*10+int(formula[i]-'0'); ++i; } } //添加到上一个哈希表里面 auto tmp = record.top(); record.pop(); for(auto &[idx,j1]:tmp){ record.top()[idx]+=j1*num; } } else{ string atom = parseAtom(); int num = parseNum(); record.top()[atom] += num; // 统计原子数 } } //统计哈希表，返回 for(auto &[idx,j]:record.top()){ ret.push_back(idx); } sort(ret.begin(),ret.end()); string ree; for(auto &i:ret){ if(record.top()[i]==1){ ree+=i; }else{ ree+=i; stringstream ss; ss << record.top()[i]; string str = ss.str(); ree+=str; } } return ree; } };

• 394. 字符串解码

  给定一个经过编码的字符串，返回它解码后的字符串。

  编码规则为: k[encoded_string]，表示其中方括号内部的 encoded_string 正好重复 k 次。注意 k 保证为正整数。

  你可以认为输入字符串总是有效的；输入字符串中没有额外的空格，且输入的方括号总是符合格式要求的。

  此外，你可以认为原始数据不包含数字，所有的数字只表示重复的次数 k ，例如不会出现像 3a 或 2[4] 的输入。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35

  class Solution { public: string decodeString(string s) { //两个栈分别压int res和用pair stack<pair<int, string>> sta; int num = 0; string res = ""; //循环检查字符串 for (int i = 0; i < s.size(); i++) { //遇到数字则存入num,数字会大于100 if (s[i] >= '0'&&s[i] <= '9') { num =num*10; num += (s[i] - '0'); } else if (s[i] == '[') {//遇到[压栈数字和字符串，置零置空 sta.push(make_pair(num, res)); num = 0; res = ""; } else if (s[i] == ']') {//遇到]出栈数字和字符串，组装 int n = sta.top().first;//n指示的是res的循环次数，不是temp的 string temp = sta.top().second;//之间的 sta.pop(); for (int i = 0; i < n; i++){ temp += res; //循环n次 } //重新赋值 res = temp; } else {//遇到字符存入字符 res += s[i]; } } return res; } };

图的深度优先搜索

• 547. 省份数量

  有 n 个城市，其中一些彼此相连，另一些没有相连。如果城市 a 与城市 b 直接相连，且城市 b 与城市 c 直接相连，那么城市 a 与城市 c 间接相连。

  省份 是一组直接或间接相连的城市，组内不含其他没有相连的城市。

  给你一个 n x n 的矩阵 isConnected ，其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连，而 isConnected[i][j] = 0 表示二者不直接相连。

  返回矩阵中 省份 的数量。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33

  //思路，图的深度优先搜索，所给矩阵即为图的邻接矩阵 class Solution { public: void dfs(vector<vector<int>>& isConnected,vector<bool> &visited,int city,int i){ if(!visited[i]){ //标记这个城市找过了 visited[i]=true; for(int j=0;j<city;++j){ if(isConnected[i][j]==1){ //深度优先搜索 dfs(isConnected, visited, city, j); } } } } int findCircleNum(vector<vector<int>>& isConnected) { int city=isConnected.size();//城市总数 vector<bool> visited(city,false);//判断是否走过的向量 int provience=0; //i行,i个城市 for(int i=0;i<city;++i){ if(!visited[i]){ //深搜找关联城市并标记 dfs(isConnected,visited,city,i); ++provience; } } return provience; } };

BFS:广度优先搜索

• DFS 深度优先算法就是回溯算法

• BFS 的核心思想应该不难理解的，就是把一些问题抽象成图，从一个点开始，向四周开始扩散。一般来说，我们写 BFS 算法都是用「队列」queue这种数据结构，每次将一个节点周围的所有节点加入队列。

• 相对来说，DFS用的数据结构就是「栈」stack

• 127. 单词接龙

  字典 wordList 中从单词 beginWord 和 endWord 的 转换序列 是一个按下述规格形成的序列 beginWord -> s1 -> s2 -> ... -> sk：

  • 每一对相邻的单词只差一个字母。
  • 对于 1 <= i <= k 时，每个 si 都在 wordList 中。注意， beginWord 不需要在 wordList 中。
  • sk == endWord

  给你两个单词 beginWord 和 endWord 和一个字典 wordList ，返回 从 beginWord 到 endWord 的 最短转换序列 中的 单词数目 。如果不存在这样的转换序列，返回 0 。

• 思路：单向bfs会超时，因为第一次建图采用的是暴力，每个字符都和其他字符判断，是否只有一个字符不同，超时。所以要想怎么优化建图，解答有使用虚拟节点建图的，这里采用所有字符都变换成a-z ，哈希表判断是否存在判断图的边。值得注意的是，这是动态建图的，一边bfs一边建图

• 其他解答——1.虚拟节点建图；2.双向bfs

• 使用一个visited数组判断就行，第一次的肯定是最短的。也可以不用数组，用一个字符串删除一个字符串。

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72

  class Solution { public: //使用1个visited数组就行了，第一次访问到的肯定是最小的 //单向bfs int ladderLength(string beginWord, string endWord, vector<string> &wordList) { unordered_map<string, int> checkOk; int n = wordList.size(); for (int i = 0; i < n; ++i) { checkOk[wordList[i]] = i; } if (!checkOk.count(endWord)) { return 0; } //建图 int target = checkOk[endWord]; queue<int> bfs; vector<bool> visited(n); int wordLen = beginWord.size(); //初始化队列 for (int i = 0; i < beginWord.size(); ++i) { string temp1 = beginWord; char src = temp1[i]; for (char j = 0; j < 26; ++j) { char change = 'a' + j; if (change == src) { continue; } temp1[i] = change; if (checkOk.count(temp1)) { if(checkOk[temp1]==target){ return 2; } bfs.emplace(checkOk[temp1]); visited[checkOk[temp1]] = true; } } } //开始bfs int step = 2; while (!bfs.empty()) { int n1 = bfs.size(); for (int i = 0; i < n1; ++i) { int idx = bfs.front(); bfs.pop(); if(idx == target){ return step; } //加入新的 string curr = wordList[idx]; for(int k = 0;k<wordLen;++k){ string temp1 = curr; char src = temp1[k]; for (char j = 0; j < 26; ++j) { char change = 'a' + j; if (change == src) { continue; } temp1[k] = change; if (checkOk.count(temp1)&&!visited[checkOk[temp1]]) { bfs.emplace(checkOk[temp1]); visited[checkOk[temp1]] = true; } } } } ++step; } return 0; } };

• 解法2——优化建图，虚拟节点，类似无向图构建双向的，遍历一次所有节点即可完成构图，哈希表存储id。

• 具体地，我们可以创建虚拟节点。对于单词 hit，我们创建三个虚拟节点 *it、h*t、hi*，并让 hit 向这三个虚拟节点分别连一条边即可。如果一个单词能够转化为 hit，那么该单词必然会连接到这三个虚拟节点之一。对于每一个单词，我们枚举它连接到的虚拟节点，把该单词对应的 id 与这些虚拟节点对应的 id 相互相连即可。

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66

  class Solution { public: unordered_map<string, int> wordId; vector<vector<int>> edge; int nodeNum = 0; void addWord(string &word) { if (!wordId.count(word)) { wordId[word] = nodeNum++; edge.emplace_back(); } } void addEdge(string &word) { addWord(word); int id1 = wordId[word]; //直接引用改变 for (char &it : word) { char tmp = it; it = '*'; addWord(word); int id2 = wordId[word]; //无向图，双向赋值，虚拟节点 edge[id1].push_back(id2); edge[id2].push_back(id1); //恢复原始字符串 it = tmp; } } int ladderLength(string beginWord, string endWord, vector<string> &wordList) { for (string &word : wordList) { addEdge(word); } addEdge(beginWord); if (!wordId.count(endWord)) { return 0; } int beginId = wordId[beginWord], endId = wordId[endWord]; int step = 0; queue<int> que; que.push(beginId); unordered_set<int> check_visited; while (!que.empty()) { int n = que.size(); for (int kk = 0; kk < n; ++kk) { int x = que.front(); que.pop(); if (x == endId) { return step / 2 + 1; } for (int &it : edge[x]) { if (check_visited.count(it)) { continue; } else { check_visited.insert(it); que.push(it); } } } ++step; } return 0; } };

• 111. 二叉树的最小深度

  给定一个二叉树，找出其最小深度。

  最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

  说明: 叶子节点是指没有子节点的节点。

• 思路1：BFS，很简单

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43

  /** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: int minDepth(TreeNode* root) { if(!root){ return 0; } queue<TreeNode*> bfs; bfs.push(root); int height=1; while(!bfs.empty()){ int num=bfs.size(); int i=0; for(;i<num;++i){ TreeNode* temp=bfs.front(); bfs.pop(); if(!temp->left&&!temp->right){ return height;//直接返回 break; } if(temp->left){ bfs.push(temp->left); } if(temp->right){ bfs.push(temp->right); } } ++height;//遍历完一层再+1 } return height; } };

• 思路2，DFS，有些绕，但是可以想

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

  class Solution { public: int minDepth(TreeNode* root) { if(!root){ return 0; } //计算左子树深度 int left = minDepth(root->left); //计算右子树深度 int right = minDepth(root->right); //如果左右子树存在一个为0，那个当前树的最小深度是其中一颗子树深度+1，因为另外一颗肯定是0，所以left+right+1 //如果都bu为0，那么就是最小深度+1 return left==0 || right==0 ? (left+right+1):min(left,right)+1; } };

• 286. 墙与门

  你被给定一个 m × n 的二维网格 rooms ，网格中有以下三种可能的初始化值：

  1. -1 表示墙或是障碍物
  2. 0 表示一扇门
  3. INF 无限表示一个空的房间。然后，我们用 231 - 1 = 2147483647 代表 INF。你可以认为通往门的距离总是小于 2147483647 的。

  你要给每个空房间位上填上该房间到 最近门的距离 ，如果无法到达门，则填 INF 即可。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41

  class Solution { public: const int room=2147483647; const vector<int> dx{1,-1,0,0}; const vector<int> dy{0,0,1,-1}; void wallsAndGates(vector<vector<int>>& rooms) { queue<pair<int,int>> dp; int rows=rooms.size(); int cols=rooms[0].size(); for(int i=0;i<rows;++i){ for(int j=0;j<cols;++j){ if(rooms[i][j]==0){ dp.emplace(pair<int,int>{i,j}); } } } int step=1; int n; while(!dp.empty()){ n=dp.size(); while(n>0){ auto temp=dp.front(); dp.pop(); int oriRow=temp.first; int oriCol=temp.second; for(int i=0;i<4;++i){ int newrow=oriRow+dx[i]; int newcol=oriCol+dy[i]; if(newrow>=0&&newrow<rows&&newcol>=0&&newcol<cols){ if(rooms[newrow][newcol]==room){ dp.emplace(newrow,newcol); rooms[newrow][newcol]=step; } } } n--; } ++step; } } };

• 417. 太平洋大西洋水流问题

  有一个 m × n 的长方形岛屿，与 太平洋 和 大西洋 相邻。 “太平洋” 处于大陆的左边界和上边界，而 “大西洋” 处于大陆的右边界和下边界。

  这个岛被分割成一个个方格网格。给定一个 m x n 的整数矩阵 heights ， heights[r][c] 表示坐标 (r, c) 上单元格 高于海平面的高度 。

  岛上雨水较多，如果相邻小区的高度 小于或等于 当前小区的高度，雨水可以直接向北、南、东、西流向相邻小区。水可以从海洋附近的任何细胞流入海洋。

  返回 网格坐标 result 的 2D列表 ，其中 result[i] = [ri, ci] 表示雨水可以从单元格 (ri, ci) 流向 太平洋和大西洋 。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83

  class Solution { public: const vector<int> dx{1,-1,0,0}; const vector<int> dy{0,0,1,-1}; //两次bfs，分别表示太平洋和大西洋 vector<vector<int>> pacificAtlantic(vector<vector<int>>& heights) { vector<vector<int>> ret; int rows=heights.size(); int cols=heights[0].size(); vector<vector<bool>> pacifiCheck(rows,vector<bool>(cols,false)); vector<vector<bool>> atlanticCheck(rows,vector<bool>(cols,false)); //判断太平洋 queue<pair<int,int>> check; for(int i=0;i<cols;++i){ pacifiCheck[0][i]=true; check.emplace(0,i); } for(int i=1;i<rows;++i){ pacifiCheck[i][0]=true; check.emplace(i,0); } while(!check.empty()){ int n=check.size(); while(n>0){ auto temp=check.front(); check.pop(); int orirow=temp.first; int oricol=temp.second; for(int i=0;i<4;++i){ int newrow=orirow+dx[i]; int newcol=oricol+dy[i]; if(newrow>=0&&newcol>=0&&newrow<rows&&newcol<cols){ if(!pacifiCheck[newrow][newcol]&&heights[newrow][newcol]>=heights[orirow][oricol]){ pacifiCheck[newrow][newcol]=true; check.emplace(newrow,newcol); } } } n--; } } //判断大西洋 for(int i=0;i<cols;++i){ atlanticCheck[rows-1][i]=true; check.emplace(rows-1,i); } for(int i=0;i<(rows-1);++i){ atlanticCheck[i][cols-1]=true; check.emplace(i,cols-1); } while(!check.empty()){ int n=check.size(); while(n>0){ auto temp=check.front(); check.pop(); int orirow=temp.first; int oricol=temp.second; for(int i=0;i<4;++i){ int newrow=orirow+dx[i]; int newcol=oricol+dy[i]; if(newrow>=0&&newcol>=0&&newrow<rows&&newcol<cols){ if(!atlanticCheck[newrow][newcol]&&heights[newrow][newcol]>=heights[orirow][oricol]){ atlanticCheck[newrow][newcol]=true; check.emplace(newrow,newcol); } } } n--; } } //总 for(int i=0;i<rows;++i){ for(int j=0;j<cols;++j){ if(pacifiCheck[i][j]&&atlanticCheck[i][j]){ ret.emplace_back(vector<int>{i,j}); } } } return ret; } };

• 752. 打开转盘锁

  你有一个带有四个圆形拨轮的转盘锁。每个拨轮都有10个数字： '0', '1', '2', '3', '4', '5', '6', '7', '8', '9' 。每个拨轮可以自由旋转：例如把 '9' 变为 '0'，'0' 变为 '9' 。每次旋转都只能旋转一个拨轮的一位数字。

  锁的初始数字为 '0000' ，一个代表四个拨轮的数字的字符串。

  列表 deadends 包含了一组死亡数字，一旦拨轮的数字和列表里的任何一个元素相同，这个锁将会被永久锁定，无法再被旋转。

  字符串 target 代表可以解锁的数字，你需要给出解锁需要的最小旋转次数，如果无论如何不能解锁，返回 -1 。

  • 思路：看出一棵树，8叉树，每位数字有两种上下旋转的方式，四位就是8种，广度优先遍历，层数最少即返回

  • 需要注意重复的节点不走

  • 死亡节点不走

  • 以下是典型套路，记住这些模板即可

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71

  class Solution { public: int openLock(vector<string>& deadends, string target) { if(target=="0000"){ return 0; } //哈希判断死区 unordered_set<string> dead(deadends.begin(),deadends.end()); if(dead.count(target)){ return -1; } //已经看过的字符串，防止重复 unordered_set<string> visited; //初始化 visited.insert("0000"); queue<string> bfs; bfs.push("0000"); int step=0; //开始遍历 while(!bfs.empty()){ int n=bfs.size(); for(int i=0;i<n;++i){ string temp=bfs.front(); bfs.pop(); //判断到达终点 if(dead.count(temp)){ continue; } if(temp==target){ return step; } //修改数字 for(int j=0;j<4;++j){ //上转 string up=turn_up(j,temp); if(!visited.count(up)){ bfs.push(up); visited.insert(up);//记得加入已经遍历过了 } //下转 string down=turn_down(j, temp); if(!visited.count(down)){ bfs.push(down); visited.insert(down); } } } //增加层数 ++step; } return -1; } string turn_up(int j,string input){ if(input[j]=='0'){ input[j]='9'; }else{ input[j]-=1; } return input; } string turn_down(int j, string input){ if(input[j]=='9'){ input[j]='0'; }else{ input[j]+=1; } return input; } };

• 542. 01 矩阵

  给定一个由 0 和 1 组成的矩阵 mat ，请输出一个大小相同的矩阵，其中每一个格子是 mat 中对应位置元素到最近的 0 的距离。

  两个相邻元素间的距离为 1 。

  • 有两种思路：广度优先搜索和DP
  • DP思路：
    • 设置四个dp数组，依次表示左下、左上、右下、右上的最短距离，最后比较四个数组得出最短即可
    • 优化：可以只需要左下和右上两个dp数组即可，因为只有0-1两种可能，不会存在“π”这种路径，所以可以遍历从左上角到右下角和从右下角到左上角即可，因为这样已经包含了上下左右四个方向的信息了。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46

  class Solution { public: //思路：最短距离，采用广度优先搜索，队列 //逆向思维：从0开始，依次层序遍历，每次步数加1 const vector<int> dx{0,0,1,-1}; const vector<int> dy{1,-1,0,0}; vector<vector<int>> updateMatrix(vector<vector<int>>& mat) { int rows=mat.size(); int cols=mat[0].size(); vector<vector<int>> ret(rows,vector<int>(cols,-1)); //初始化0 queue<pair<int,int>> bfs; for(int i=0;i<rows;++i){ for(int j=0;j<cols;++j){ if(mat[i][j]==0){ bfs.push(pair<int,int>(i,j)); ret[i][j]=0; } } } int step=1; while(!bfs.empty()){ int n=bfs.size(); for(int i=0;i<n;++i){ auto temp=bfs.front(); bfs.pop(); for(int j=0;j<4;++j){ int newrow=temp.first+dx[j]; int newcol=temp.second+dy[j]; if(newrow>=0&&newrow<rows&&newcol>=0&&newcol<cols){ if(ret[newrow][newcol]!=-1){ continue; } ret[newrow][newcol]=step; //入队 bfs.push(pair<int,int>(newrow,newcol)); } } } ++step; } return ret; } };

• 994. 腐烂的橘子

  在给定的网格中，每个单元格可以有以下三个值之一：

  • 值 0 代表空单元格；
  • 值 1 代表新鲜橘子；
  • 值 2 代表腐烂的橘子。

  每分钟，任何与腐烂的橘子（在 4 个正方向上）相邻的新鲜橘子都会腐烂。

  返回直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能，返回 -1。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57

  //思路，多源广度优先搜素 class Solution { public: const vector<int> dx{0,0,1,-1}; const vector<int> dy{1,-1,0,0}; int orangesRotting(vector<vector<int>>& grid) { int rows=grid.size(); int cols=grid[0].size(); //判断全零 int fresh=0; queue<pair<int,int>> bfs; for(int i=0;i<rows;++i){ for(int j=0;j<cols;++j){ if(grid[i][j]==2){ bfs.push(pair<int,int>(i,j)); } if(grid[i][j]==1){ fresh++; } } } if(fresh==0 && bfs.empty()){ return 0; } //判断又好有坏 int step=0; while(!bfs.empty()){ int n=bfs.size(); for(int i=0;i<n;++i){ auto temp=bfs.front(); bfs.pop(); for(int j=0;j<4;++j){ int newrow=temp.first+dx[j]; int newcol=temp.second+dy[j]; if(newrow>=0&&newrow<rows&&newcol>=0&&newcol<cols){ if(grid[newrow][newcol]==1){ grid[newrow][newcol]=2; bfs.push(pair<int,int>(newrow,newcol)); } } } } ++step; } for(int i=0;i<rows;++i){ for(int j=0;j<cols;++j){ if(grid[i][j]==1){ return -1; } } } //减去最后加的那层 return step-1; } };

• 1091. 二进制矩阵中的最短路径

  给你一个 n x n 的二进制矩阵 grid 中，返回矩阵中最短 畅通路径 的长度。如果不存在这样的路径，返回 -1 。

  二进制矩阵中的 畅通路径 是一条从 左上角 单元格（即，(0, 0)）到 右下角 单元格（即，(n - 1, n - 1)）的路径，该路径同时满足下述要求：

  • 路径途经的所有单元格都的值都是 0 。
  • 路径中所有相邻的单元格应当在 8 个方向之一 上连通（即，相邻两单元之间彼此不同且共享一条边或者一个角）。

  畅通路径的长度 是该路径途经的单元格总数。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38

  class Solution { public: const vector<int> dx{0,0,1,1,1,-1,-1,-1}; const vector<int> dy{1,-1,0,1,-1,0,1,-1}; int shortestPathBinaryMatrix(vector<vector<int>>& grid) { int n=grid.size(); if(grid[0][0]!=0||grid[n-1][n-1]){ return -1; } int step=1; queue<pair<int,int>> bfs; bfs.push(pair<int,int>(0,0)); while(!bfs.empty()){ int s_t=bfs.size(); for(int i=0;i<s_t;++i){ pair<int,int> temp=bfs.front(); bfs.pop(); if(grid[temp.first][temp.second]==0){ if(temp.first==n-1&&temp.second==n-1){ return step; } //判断已经走过了 grid[temp.first][temp.second]=1; for(int j=0;j<8;++j){ int newrow=temp.first+dx[j]; int newcol=temp.second+dy[j]; if(newrow>=0&&newrow<n&&newcol>=0&&newcol<n){ bfs.push(pair<int,int>(newrow,newcol)); } } } } ++step; } return -1; } };

• LCP 09. 最小跳跃次数

  为了给刷题的同学一些奖励，力扣团队引入了一个弹簧游戏机。游戏机由 N 个特殊弹簧排成一排，编号为 0 到 N-1。初始有一个小球在编号 0 的弹簧处。若小球在编号为 i 的弹簧处，通过按动弹簧，可以选择把小球向右弹射 jump[i] 的距离，或者向左弹射到任意左侧弹簧的位置。也就是说，在编号为 i 弹簧处按动弹簧，小球可以弹向 0 到 i-1 中任意弹簧或者 i+jump[i] 的弹簧（若 i+jump[i]>=N ，则表示小球弹出了机器）。小球位于编号 0 处的弹簧时不能再向左弹。

  为了获得奖励，你需要将小球弹出机器。请求出最少需要按动多少次弹簧，可以将小球从编号 0 弹簧弹出整个机器，即向右越过编号 N-1 的弹簧。

• 一般的bfs的复杂度是O(N^2)，但是添加far变量保持上一次的走到的最值之后，可以保证复杂度变成O(n)。

• 一种新的思路，bfs高度不一样要用size，也可以直接保存一个变量step。

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39

  class Solution { public: int minJump(vector<int>& jump) { //使用bfs int n = jump.size(); int far = 0;//避免重复判断，进一步优化，是的n方变成n vector<bool> visited(n,false);//避免重复判断， visited[0] = true; queue<pair<int,int>> bfs;//第一个是位置，第二个是步数 bfs.emplace(pair<int,int>{0,1});//初始化第一步就是1 while(!bfs.empty()){ auto temp =bfs.front(); bfs.pop(); int idx = temp.first; int step = temp.second; if(idx+jump[idx]>=n){ return step; break; } //否则插入 if(!visited[idx+jump[idx]]){ bfs.emplace(pair<int,int>{idx+jump[idx],step+1}); visited[idx+jump[idx]]=true; } //插入左边 for(int i=far;i<idx;++i){ if(!visited[i]){ bfs.emplace(pair<int,int>{i,step+1}); visited[i]=true; } } //更新far far=max(far,idx+1); } return -1; } };

二分查找

• 二分查找不简单，Knuth 大佬（发明 KMP 算法的那位）都说二分查找：思路很简单，细节是魔鬼。很多人喜欢拿整型溢出的 bug 说事儿，但是二分查找真正的坑根本就不是那个细节问题，而是在于到底：

  • 要给mid加一还是减一，
  • while 里到底用<=还是<。

• 难点——查找区间、判断函数。

• 边界条件

  • 左闭右闭[a,b]

    • 1 2 3 4 5 6 7 8

      //缺点，最后返回left+1=right，需要最后再验证 while(right-left>1){ if(){ left=mid; }else{ right=mid; } }

    • 1 2 3 4 5 6 7 8

      //全遍历，最后right>left while(right>=left){ if(){ left=mid+1; }else{ right=mid-1; } }

  • 左闭右开[a,b)

    • 1 2 3 4 5 6 7 8

      //最后返回left=right，最后得出结果 while(right>left){ if(){ left=mid+1;//[mid+1,right) }else{ right=mid;//[left,mid) } }

• 704. 二分查找

  给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26

  //框架模板 class Solution { public: int search(vector<int>& nums, int target) { int n=nums.size(); int left=0; int right=n-1; if(target<nums[0] || target>nums[n-1]){ return -1; } //注意取等于号 while(left<=right){ int mid=(left+right)/2; if(target==nums[mid]){ return mid; } else if(target>nums[mid]){ left=mid+1;//注意加+ }else if(target<nums[mid]){ right=mid-1;//注意减1 } } return -1; } };

• 278. 第一个错误的版本

  你是产品经理，目前正在带领一个团队开发新的产品。不幸的是，你的产品的最新版本没有通过质量检测。由于每个版本都是基于之前的版本开发的，所以错误的版本之后的所有版本都是错的。

  假设你有 n 个版本 [1, 2, ..., n]，你想找出导致之后所有版本出错的第一个错误的版本。

  你可以通过调用 bool isBadVersion(version) 接口来判断版本号 version 是否在单元测试中出错。实现一个函数来查找第一个错误的版本。你应该尽量减少对调用 API 的次数。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

  // The API isBadVersion is defined for you. // bool isBadVersion(int version); class Solution { public: int firstBadVersion(int n) { int left=1; int right=n; while(left<right){ int mid=left+(right-left)/2;//防止溢出 if(isBadVersion(mid)){ right=mid; }else{ left=mid+1; } } return left; } };

• 35. 搜索插入位置

  给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

  请必须使用时间复杂度为 O(log n) 的算法。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23

  class Solution { public: int searchInsert(vector<int>& nums, int target) { int n=nums.size(); int left=0; int right=n-1; while(left<right){ int mid=left+(right-left)/2; if(nums[mid]==target){ return mid; }else if(target>nums[mid]){ left=mid+1; }else{ right=mid; } } if(target>nums[left]){ return left+1; }else{ return left; } } };

• 34. 在排序数组中查找元素的第一个和最后一个位置

  给定一个按照升序排列的整数数组 nums，和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。

  如果数组中不存在目标值 target，返回 [-1, -1]。

  进阶：

  • 你可以设计并实现时间复杂度为 O(log n) 的算法解决此问题吗？

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46

  class Solution { public: int binarySearch(vector<int>& nums,int target,bool flag){ int left=0; int right=nums.size()-1; int ans=right+1;//以防只有一个数的时候 if(flag){ //找第一个大于target的 //因为要遍历所有，所以要等于，即等于的时候也要判断 while(left<=right){ int mid=left+(right-left)/2; if(nums[mid]>target){ right=mid-1; ans=mid; }else{ left=mid+1; } } }else{ //找第一个等于target的 while(left<=right){ int mid=left+(right-left)/2; if(nums[mid]>=target){ //依次取值，所以可以找到第一个等于的 right=mid-1; ans=mid; }else{ left=mid+1; } } } return ans; } vector<int> searchRange(vector<int>& nums, int target) { int left=binarySearch(nums, target,0); int right=binarySearch(nums, target, 1)-1; //双重保险 if(left>=0&&right>=0&&left<nums.size()&&right<nums.size()&&nums[left]==target&&nums[right]==target){ return vector<int>{left,right}; }else{ return vector<int>{-1,-1}; } } };

• 33. 搜索旋转排序数组

  整数数组 nums 按升序排列，数组中的值 互不相同 。

  在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 旋转，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。

  给你 旋转后 的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的下标，否则返回 -1 。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43

  class Solution { public: int search(vector<int>& nums, int target) { int n=nums.size(); if(n==0){ return -1; } if(n==1){ if(nums[0]==target){ return 0; }else{ return -1; } } int left=0; int right=n-1; //遍历所有点，所以要有等于号 while(left<=right){ int mid=left+(right-left)/2; if(nums[mid]==target){ return mid; } //证明左边是有序的 if(nums[0]<=nums[mid]){ //注意等于号，一定要包括首尾 if(nums[mid]>target&&nums[0]<=target){ right=mid-1; }else{ left=mid+1; } }else{ //注意等于号 if(nums[mid]<target&&target<=nums[n-1]){ left=mid+1; } else{ right=mid-1; } } } return -1; } };

• 74. 搜索二维矩阵

  编写一个高效的算法来判断 m x n 矩阵中，是否存在一个目标值。该矩阵具有如下特性：

  • 每行中的整数从左到右按升序排列。
  • 每行的第一个整数大于前一行的最后一个整数。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44

  class Solution { public: bool searchMatrix(vector<vector<int>>& matrix, int target) { int row=matrix.size(); int col=matrix[0].size(); int left=0;int right=row-1; if(target<matrix[0][0]||target>matrix[row-1][col-1]){ return false; } int ans=-1; //找第一个比target大的 while(left<=right){ int mid=left+(right-left)/2; if(matrix[mid][0]==target){ return true; }else if(matrix[mid][0]>target){ //一直迭代找到第一个 ans=mid; right=mid-1; }else{ left=mid+1; } } //证明没找到，那就找最后一次数目里面，谨记那个数目是加1之后的 if(ans==-1){ ans=left; } //两种情况都需减1 ans--; left=0;right=col-1; while(left<=right){ int mid=left+(right-left)/2; if(matrix[ans][mid]==target){ return true; } else if(matrix[ans][mid]>target){ right=mid-1; }else{ left=mid+1; } } return false; } };

• 153. 寻找旋转排序数组中的最小值

  已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次 旋转 后，得到输入数组。例如，原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到：

  • 若旋转 4 次，则可以得到 [4,5,6,7,0,1,2]
  • 若旋转 7 次，则可以得到 [0,1,2,4,5,6,7]

  注意，数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。

  给你一个元素值 互不相同 的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29

  class Solution { public: int findMin(vector<int>& nums) { int n=nums.size(); //找出分界点，比较第一位和分界点即可 if(n==1){ return nums[0]; } int left=0; int right=n-1; int ans=left; if(nums[left]<nums[right]){ return nums[left]; } //如果不等，说明旋转了，找出分界点 while(left<=right){ int mid=left+(right-left)/2; //证明左侧有序 if(nums[mid]>=nums[0]){ left=mid+1; ans=left; }else{ right=mid-1; } } return min(nums[0],nums[ans]); } };

• 162. 寻找峰值

  峰值元素是指其值严格大于左右相邻值的元素。

  给你一个整数数组 nums，找到峰值元素并返回其索引。数组可能包含多个峰值，在这种情况下，返回 任何一个峰值 所在位置即可。

  你可以假设 nums[-1] = nums[n] = -∞ 。

  你必须实现时间复杂度为 O(log n) 的算法来解决此问题。

  • 思路一：寻找数组的最大值，一定就是峰值
  • 思路二：二分法进行爬坡，mid>mid+1，一直往右。（其实也可以直接二分的，如果mid不是最大的，那就取左右那个最大的再二分，见1901. 找出顶峰元素 II）

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39

  class Solution { public: int findPeakElement(vector<int>& nums) { // nums.insert(nums.begin(), INT_MIN); // nums.push_back(INT_MIN); // int left=0; // int right=nums.size()-1; // int ans; // int right_size=right-1; // while(left<right){ // int mid=left+(right-left)/2; // if(nums[mid]<nums[mid+1]){ // left=mid+1; // }else{ // right=mid; // } // } // if(left==0){ // return 0; // }else{ // return left-1; // } //思路二：爬坡法，一直往右走 int left=0; int right=nums.size()-1; //因为相邻一定不等，所以一定可以退出得到left==right while(left<right){ int mid=left+(right-left)/2; if(nums[mid]<nums[mid+1]){ left=mid+1; }else{ right=mid; } } return left; } };

• 1060. 有序数组中的缺失元素

  • 现有一个按 升序 排列的整数数组 nums ，其中每个数字都 互不相同 。

    给你一个整数 k ，请你找出并返回从数组最左边开始的第 k 个缺失数字。

  • 两种思路，一种线性查找，先计算每一个的缺失总数和k的大小比较；一种是二分查找，不过这个二分查找比较隐秘，因为要得出需要的数组，才能查找

    

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

  //思路一：线性查找 class Solution { public: int missingElement(vector<int>& nums, int k) { int n=nums.size(); if(n==1){ return nums[0]+k; } int sum=0; int i=1; while(i<n){ sum+=nums[i]-nums[i-1]-1; if(sum>=k){ return nums[i]-((sum-k)+1); } ++i; } return nums[n-1]+(k-sum); } };

  • 思路二：二分查找

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34

  class Solution { public: //该函数计算每个位置的缺失数，进而跟k比较 int missing_count(int idx,vector<int>& nums){ return nums[idx]-nums[0]-idx; } int missingElement(vector<int>& nums, int k) { int left=0; int right=nums.size()-1; //排除开头和结尾的特殊情况 if(left==right){ return nums[0]+k; } if(missing_count(right, nums)<k){ return nums[right]+(k-missing_count(right, nums)); } //查找第一个大于左边小于等于右边的位置 int count; while(left<right){ int mid=left+(right-left)/2; count=missing_count(mid, nums); if(count<k){ left=mid+1; }else{ right=mid; } } count=missing_count(left, nums); return nums[left]-(count-k+1); } };

• 1901. 找出顶峰元素 II

  一个 2D 网格中的 顶峰元素 是指那些 严格大于 其相邻格子(上、下、左、右)的元素。

  给你一个 从 0 开始编号 的 m x n 矩阵 mat ，其中任意两个相邻格子的值都 不相同 。找出 任意一个 顶峰元素 mat[i][j] 并 返回其位置 [i,j] 。

  你可以假设整个矩阵周边环绕着一圈值为 -1 的格子。

  要求必须写出时间复杂度为 O(m log(n)) 或 O(n log(m)) 的算法

  • 思路：首先确定需求，mat数组的最大值肯定是峰值，但是这样复杂度就是O(mn)，所以要优化，每一行直接求最值O(m)，但行与行之间使用爬坡法进行二分搜索，减少复杂度。注意这里的爬坡存在mid和mid+1元素相等的情况，需要进一步判断。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51

  class Solution { public: //行进行爬坡法二分搜索O(log(n))，最大列直接O(m) //爬坡法适用相邻不同的，这里存在相同的情况，需要优化 //寻找行最大值的列数 int FindMaxCol(int row, vector<vector<int>>& mat){ int col=0; int temp=mat[row][col]; for(int i=1;i<mat[0].size();++i){ if(mat[row][i]>temp){ temp=mat[row][i]; col=i; } } return col; } vector<int> findPeakGrid(vector<vector<int>>& mat) { int start=0; int end=mat.size()-1; while(start<end){ int mid=start+(end-start)/2; int midcol=FindMaxCol(mid,mat); int downcol=FindMaxCol(mid+1,mat); if(mat[mid][midcol]<mat[mid+1][downcol]){ start=mid+1; }else if(mat[mid][midcol]>mat[mid+1][downcol]){ end=mid; }else{ //当下一个和上面相等时，判断上一个是否最大的 int topcol=FindMaxCol(mid-1,mat); int max_top=mid-1>=0?mat[mid-1][topcol]:-1; //比中间小，中间就是弱峰 if(max_top<mat[mid][midcol]){ start=mid; break; } //比中间大，上一行和首行之间是有顶峰 else{ end=mid-1; } } } int colend=FindMaxCol(start,mat); return vector<int>{start,colend}; } };

最小化最大值问题

• 410. 分割数组的最大值

  给定一个非负整数数组 nums 和一个整数 m ，你需要将这个数组分成 m 个非空的连续子数组。

  设计一个算法使得这 m 个子数组各自和的最大值最小。

  • 思路：同分享巧克力

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67

  class Solution { public: //mid是计算的边界，m是分割的数量，out是实际的mid bool check(vector<int>& nums,int mid,int m,int &out){ long long sum=0; int cnt=1; int ret=0; for(int i=0;i<nums.size();++i){ if(sum+nums[i]>mid){ ++cnt; if(sum>ret){ ret=sum; } sum=nums[i];//重新赋值,回溯 }else{ sum+=nums[i]; } } //最后更新一下，因为最后的cnt不算了，已经是默认分组 if(sum>ret){ ret=sum; } //返回最大值 out=ret; //小于等于分组数，说明mid过大，压缩right if(cnt<=m){ return true; }else{ return false; } } int splitArray(vector<int>& nums, int m) { int rows=nums.size(); vector<int> sub(rows,0); sub[0]=nums[0]; int ret=sub[0]; for(int i=1;i<rows;++i){ sub[i]=sub[i-1]+nums[i]; ret=max(ret,nums[i]); } if(rows==m){ return ret; } if(m==1){ return sub[rows-1]; } //二分查找 int left=ret; int right=sub[rows-1]; int ret2=INT_MAX; while(left<=right){ int mid=left+(right-left)/2; //最小化最大值,压缩右边 int out; if(check(nums, mid, m,out)){ right=mid-1; ret2=min(ret2,out); }else{ left=mid+1; } } return ret2; } };

最大化最小值问题

• 1231. 分享巧克力

  你有一大块巧克力，它由一些甜度不完全相同的小块组成。我们用数组 sweetness 来表示每一小块的甜度。

  你打算和 K 名朋友一起分享这块巧克力，所以你需要将切割 K 次才能得到 K+1 块，每一块都由一些 连续 的小块组成。

  为了表现出你的慷慨，你将会吃掉 总甜度最小 的一块，并将其余几块分给你的朋友们。

  请找出一个最佳的切割策略，使得你所分得的巧克力 总甜度最大，并返回这个 最大总甜度。

  • 示例

  • 输入：sweetness = [1,2,3,4,5,6,7,8,9], K = 5 输出：6 解释：你可以把巧克力分成 [1,2,3], [4,5], [6], [7], [8], [9]。

  • 思路：类似《挑战程序设计竞赛》的二分查找的最大化最小值问题一样。

    • 第一点查找区间：我可以吃的巧克力甜度在一个区间内【min(sweetness), sum(sweetness)】，显然这个区间是一个单调区间。所以可以考虑使用二分查找。

    • 第二点判断函数。在普通的二分查找中，判断函数就是 nums[mid] > target 。在这道题中，判断函数就是将 sweetness 分解成k+1个子序列，且每个子序列的和必须大于等于mid。所以判断函数可以用一个循环，从0~len，一边遍历一遍累加，当累加和sum大于等于mid时，k--，sum=0。最后返回k是否小于等于0即可，当k小于等于0说明当前mid是可以被满足的，需要向右移动寻找最大的mid。还需要注意，mid只是一个最低限度，并不一定是一个真实存在的答案，所以需要在判断函数中去寻找最小的累加和sum，这个sum才是最终的答案。sum >= mid。

    • 简单来讲——之前的思路是先确定如何切巧克力，再从最优切法中找到最小的块；但我们不妨反过来想，我们可以先确定最小的块大小，再去检查能否这样切巧克力？

      我们先写一个检查能否这样切巧克力的函数，逻辑很简单，只要切出了k+1块，即可返回TRUE。若是切到了最后一个小块还没切出，那么返回FALSE。

  • 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48

    class Solution { public: //最大化最小值问题,初始化real_div是最大值 bool check_divSweet(int k,vector<int>& sweetness,int target,int &real_div){ int n=sweetness.size(); int sum=0; for(int i=0;i<n;++i){ sum+=sweetness[i]; if(sum>=target){ real_div=min(real_div,sum); sum=0; --k; } } //只有小于0，完全可分，才可以 if(k<0){ return true; } return false; } int maximizeSweetness(vector<int>& sweetness, int k) { int right=0; int left=sweetness[0]; for(auto &i:sweetness){ right+=i; left=min(left,i); } if(k==0){ return right; } int out=left; int mid; while(right>=left){ mid=left+(right-left)/2; int ret=INT_MAX; if(check_divSweet(k, sweetness, mid, ret)){ left=mid+1; out=max(out,ret); }else{ right=mid-1; } } return out; } };

• 4. 寻找两个正序数组的中位数

  给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。

  算法的时间复杂度应该为 O(log (m+n)) 。

  • 我是用归并求的，二分查找看看解答了解就好

  • 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53

    class Solution { public: void merge(vector<int>& nums1,vector<int>& nums2,vector<int> &ret){ int left=0; int leftBoard=nums1.size(); int right=0; int rightBoard=nums2.size(); int count=0; while(left<leftBoard&&right<rightBoard){ if(nums1[left]<nums2[right]){ ret[count]=nums1[left]; ++left; ++count; }else{ ret[count]=nums2[right]; ++right; ++count; } } if(left==leftBoard){ while(right<rightBoard){ ret[count]=nums2[right]; ++right; ++count; } }else if(right==rightBoard){ while(left<leftBoard){ ret[count]=nums1[left]; ++left; ++count; } } } double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) { int n=nums1.size(); int m=nums2.size(); int last=m+n; vector<int> ret; ret.resize(last); merge(nums1, nums2, ret); if(last%2==0){ double mid1=ret[last/2]; double mid2=ret[last/2-1]; double get=((mid1+mid2)/2); return get; }else{ return ret[last/2]; } } };

  • 

  • 

  • 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45

    class Solution { public: int getKthElement(const vector<int>& nums1, const vector<int>& nums2, int k) { /* 主要思路：要找到第 k (k>1) 小的元素，那么就取 pivot1 = nums1[k/2-1] 和 pivot2 = nums2[k/2-1] 进行比较 * 这里的 "/" 表示整除 * nums1 中小于等于 pivot1 的元素有 nums1[0 .. k/2-2] 共计 k/2-1 个 * nums2 中小于等于 pivot2 的元素有 nums2[0 .. k/2-2] 共计 k/2-1 个 * 取 pivot = min(pivot1, pivot2)，两个数组中小于等于 pivot 的元素共计不会超过 (k/2-1) + (k/2-1) <= k-2 个 * 这样 pivot 本身最大也只能是第 k-1 小的元素 * 如果 pivot = pivot1，那么 nums1[0 .. k/2-1] 都不可能是第 k 小的元素。把这些元素全部 "删除"，剩下的作为新的 nums1 数组 * 如果 pivot = pivot2，那么 nums2[0 .. k/2-1] 都不可能是第 k 小的元素。把这些元素全部 "删除"，剩下的作为新的 nums2 数组 * 由于我们 "删除" 了一些元素（这些元素都比第 k 小的元素要小），因此需要修改 k 的值，减去删除的数的个数 */ int m = nums1.size(); int n = nums2.size(); int index1 = 0, index2 = 0; while (true) { // 边界情况 if (index1 == m) { return nums2[index2 + k - 1]; } if (index2 == n) { return nums1[index1 + k - 1]; } if (k == 1) { return min(nums1[index1], nums2[index2]); } // 正常情况 int newIndex1 = min(index1 + k / 2 - 1, m - 1); int newIndex2 = min(index2 + k / 2 - 1, n - 1); int pivot1 = nums1[newIndex1]; int pivot2 = nums2[newIndex2]; if (pivot1 <= pivot2) { k -= newIndex1 - index1 + 1; index1 = newIndex1 + 1; } else { k -= newIndex2 - index2 + 1; index2 = newIndex2 + 1; } } }

C++自带的二分查找函数+哈希

• 2080. 区间内查询数字的频率

  请你设计一个数据结构，它能求出给定子数组内一个给定值的 频率 。

  子数组中一个值的 频率 指的是这个子数组中这个值的出现次数。

  请你实现 RangeFreqQuery 类：

  • RangeFreqQuery(int[] arr) 用下标从 0 开始的整数数组 arr 构造一个类的实例。
  • int query(int left, int right, int value) 返回子数组 arr[left...right] 中 value 的 频率 。

  一个 子数组 指的是数组中一段连续的元素。arr[left...right] 指的是 nums 中包含下标 left 和 right 在内 的中间一段连续元素。

• 

• 第一步采用哈希表；第二步采用二分查找

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

  class RangeFreqQuery { public: unordered_map<int,vector<int>> dp; RangeFreqQuery(vector<int>& arr) { for(int i = 0;i<arr.size();++i){ dp[arr[i]].emplace_back(i); } } int query(int left, int right, int value) { int count = 0; if(!dp.count(value)){ return count; } auto i1 = lower_bound(dp[value].begin(),dp[value].end(), left);//第一个大于等于 auto i2 = upper_bound(dp[value].begin(),dp[value].end(), right);//第一个大于 return i2-i1; } };

• 自己写的二分查找，第一个大于等于用全闭合区间，第二个大于用左开右闭区间

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76

  class RangeFreqQuery { public: unordered_map<int,vector<int>> dp; //第一个大于等于,无重复，肯定存在 int getLower(vector<int> &nums,int value){ int left = 0; int right = nums.size()-1; if(nums[left]>=value){ return left; } //必要的 if(nums[right]<value){ return right+1;// } //左右闭合区间 while(left<=right){ int mid = left+(right-left)/2; if(nums[mid]>value){ right =mid-1; }else if(nums[mid]==value){ return mid; }else{ left = mid+1; } } if(nums[right]>value){ return right; }else{ return right+1; } } //第一个大于,无重复，肯定存在 int getUpper(vector<int> &nums,int value){ int left = 0; int right = nums.size()-1; if(nums[left]>value){ return left; } //必要的，多一位 if(nums[right]<=value){ return right+1;//0表示没找到 } while(left<right){ int mid = left+(right-left)/2; if(nums[mid]>value){ right =mid; }else if(nums[mid]<=value){ left = mid+1; } } return right;//左开右闭 } RangeFreqQuery(vector<int>& arr) { for(int i = 0;i<arr.size();++i){ dp[arr[i]].emplace_back(i); } } int query(int left, int right, int value) { int count = 0; if(!dp.count(value)){ return count; } int i1 = getLower(dp[value], left);//第一个大于等于 int i2 = getUpper(dp[value], right);//第一个大于 return i2-i1; } };

动态规划（dp）

• 首先，动态规划问题的一般形式就是求最值。动态规划其实是运筹学的一种最优化方法，只不过在计算机问题上应用比较多，比如说让你求最长递增子序列呀，最小编辑距离呀等等。
• 基本思路是穷举法
• 三点概念
  • 重叠子问题——所以可以优化。
  • 状态转移方程——数学表达式，如何递归、迭代，如何从一种状态转向另外的状态，类似数电
  • 最优子结构：最优子结构指的是，问题的最优解包含子问题的最优解。反过来说就是，我们可以通过子问题的最优解，推导出问题的最优解。
• 判断是否是动态规划问题（DP）
  • 一个问题必须具有「最优子结构」才能叫DP问题。要符合「最优子结构」，子问题间必须互相独立。
• 典型是切钢条、划分蛋糕问题。
• 自顶向下的备忘录法
• 自底向上的DP数组法
• 关键是数学归纳法的递推公式！！
• 使用动态规划解决的问题有个明显的特点，一旦一个子问题的求解得到结果，以后的计算过程就不会修改它，这样的特点叫做无后效性，求解问题的过程形成了一张有向无环图。动态规划只解决每个子问题一次，具有天然剪枝的功能，从而减少计算量。
• 动规五部曲
  • 确定dp数组（dp table）以及下标的含义
  • 确定递推公式
  • dp数组如何初始化
  • 确定遍历顺序
  • 举例推导dp数组
• 总结：贪心、动态规划的问题，大多数都是求最值，比如最长子序列，最小编辑距离，最长公共子串等等等，这就是规律，因为动态规划本身就是运筹学里的一种求最值的算法。如果遇到不是求最值，要学会转化

典型例题

• 一下是经典例题，外加0-1背包和完全背包（掌握这几种即可）

• 

• 53 最大连续子序和

  • 题干：给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

  • dp 数组的含义：

    以 nums[i] 为结尾的「最大子数组和」为 dp[i]。最后返回dp数组的最大只就是 了。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

  class Solution { public: int maxSubArray(vector<int>& nums) { int n=nums.size(); vector<int> dp(n,0); dp[0]=nums[0]; int ret=dp[0]; for(int i=1;i<n;++i){ if(dp[i-1]>0){ dp[i]=dp[i-1]+nums[i]; }else{ dp[i]=nums[i]; } if(ret<dp[i]){ ret=dp[i]; } } return ret; } };

• 152 乘积最大子数组

  • 给你一个整数数组 nums ，请你找出数组中乘积最大的连续子数组（该子数组中至少包含一个数字），并返回该子数组所对应的乘积。

• 思路：因为存在负负得正，所以维护一个最小乘积的dp数组

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

  class Solution { public: int maxProduct(vector<int>& nums) { int n=nums.size(); vector<int> dp(n),dp_min(n); dp[0]=nums[0];//以当前i元素结尾的乘积最大数组 dp_min[0]=nums[0];//以当前元素结尾的乘积最小数组 //最后返回dp数组的最大值就是了 int ret=dp[0]; for(int i=1;i<n;++i){ dp[i]=max(nums[i]*dp[i-1],max(nums[i]*dp_min[i-1],nums[i])); dp_min[i]=min(nums[i]*dp[i-1],min(nums[i]*dp_min[i-1],nums[i])); ret=max(dp[i],ret); } return ret; } };

• 300 最长递增子序列，可删减元素，但要保证严格递增（LIS）

  • 给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

    子序列是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

  • 思路：维护一个dp数组，表示前i个的以num[i]为结尾最长递增子序列，所以最后return的是dp 数组的最大值

  • 然后dp[i]=max(dp[j],j<i且nums[j]<nums[i])，和分蛋糕、分钢条很类似，复杂度O(N^2)。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

  class Solution { public: int lengthOfLIS(vector<int>& nums) { if(nums.size()==0){ return 0; } vector<int> dp(nums.size(),1); int ret=1;//保证一个元素也可以返回 for(int i=1;i<nums.size();++i){ for(int j=0;j<i;++j){ //严格递增，没有等号 if(nums[j]<nums[i]){ dp[i]=max(dp[i],dp[j]+1); } } if(ret<dp[i]){ ret=dp[i]; } } return ret; } };

• 673. 最长递增子序列的个数

  给定一个未排序的整数数组，找到最长递增子序列的个数。

  • 最长递增子序列的长度的变种问题

  • 思路：定义dp[i]为以num[i]结尾的最长上升子序列的长度，count[i]为以num[i]结尾的最长上升子序列的个数。设num的最长上升子序列为maxlen，最后 的ans为满足所有dp[i]=maxlen的i的对应的count[i]之和。

  • 

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35

  class Solution { public: //设置两个dp数组 //一个表示以当前结尾的最长递增子序列的长度，一个表示当前结尾的最长递增子序列的个数 int findNumberOfLIS(vector<int>& nums) { int n=nums.size(); vector<int> dp(n,1),count_num(n,1); //初始化 dp[0]=1; count_num[0]=1; int ans=0; int maxlen=1; //动态规划 for(int i=1;i<n;++i){ for(int j=0;j<i;++j){ if(nums[j]<nums[i]){ if(dp[j]+1>dp[i]){ dp[i]=dp[j]+1; count_num[i]=count_num[j];//更新最长序列，所以也要更新个数 }else if(dp[j]+1==dp[i]){ count_num[i]+=count_num[j];//一定要先更新后叠加，不然会重复叠加 } } } maxlen=max(maxlen,dp[i]); } for(int i=0;i<n;++i){ if(dp[i]==maxlen){ ans+=count_num[i]; } } return ans; } };

• 1048. 最长字符串链

  给出一个单词列表，其中每个单词都由小写英文字母组成。

  如果我们可以在 word1 的任何地方添加一个字母使其变成 word2，那么我们认为 word1 是 word2 的前身。例如，"abc" 是 "abac" 的前身。

  词链是单词 [word_1, word_2, ..., word_k] 组成的序列，k >= 1，其中 word_1 是 word_2 的前身，word_2 是 word_3 的前身，依此类推。

  从给定单词列表 words 中选择单词组成词链，返回词链的最长可能长度。

  • 思路：最长递增子序列的变形
  • 先按字符串长度排序，然后依次比较，定义dp[i]为以word[i]结尾的词链的最长长度。最后返回dp数组的最大值即可

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40

  class Solution { public: bool check(string &a,string &b){ //a>b int n1=a.size(); int n2=b.size(); if(n1==n2+1){ string temp; for(int i=0;i<n1;++i){ temp.assign(a); temp.erase((temp.begin()+i)); if(b==temp){ return true; } temp.clear(); } } return false; } int longestStrChain(vector<string>& words) { int n=words.size(); vector<int> dp(n,0); dp[0]=1; sort(words.begin(),words.end(),[](string &a,string&b){ return a.size()<b.size(); }); int ret=1; for(int i=1;i<n;++i){ dp[i]=1; for(int j=0;j<i;++j){ if(check(words[i], words[j])){ dp[i]=max(dp[i],dp[j]+1); } } ret=max(ret,dp[i]); } return ret; } };

• 718. 最长重复子数组

  给两个整数数组 nums1 和 nums2 ，返回 两个数组中 公共的 、长度最长的子数组的长度 。

• 思路1：使用动规，dp[a][b]数组的含义是以nums1[a]和nums2[b] 结尾的子数组的长度。返回矩阵的最值就是答案

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35

  class Solution { public: int findLength(vector<int>& nums1, vector<int>& nums2) { int n1 = nums1.size(); int n2 = nums2.size(); vector<vector<int>> dp(n1,vector<int>(n2,0)); int ret =0; //初始化第一行 for(int i = 0;i<n2;++i){ if(nums2[i] == nums1[0]){ dp[0][i]=1; ret =1; } } for(int i = 0;i<n1;++i){ if(nums1[i] == nums2[0]){ dp[i][0]=1; ret =1; } } //开始动规 for(int row =1;row<n1;++row){ for(int col =1;col<n2;++col){ if(nums1[row] == nums2[col]){ dp[row][col]=dp[row-1][col-1]+1; }else{ dp[row][col]=0; } ret =max(ret,dp[row][col]); } } return ret; } };

• 滑动窗口做法

• 类似卷积

• 

• 我们可以枚举 A 和 B 所有的对齐方式。对齐的方式有两类：第一类为 A 不变，B 的首元素与 A 中的某个元素对齐；第二类为 B 不变，A 的首元素与 B 中的某个元素对齐。对于每一种对齐方式，我们计算它们相对位置相同的重复子数组即可。

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33

  class Solution { public: //依次是A的偏移量，B的偏移量，判断的长度 int maxLength(vector<int>& A, vector<int>& B, int addA, int addB, int len) { int ret = 0, k = 0; for (int i = 0; i < len; i++) { if (A[addA + i] == B[addB + i]) { k++; } else { k = 0; } ret = max(ret, k); } return ret; } int findLength(vector<int>& A, vector<int>& B) { int n = A.size(), m = B.size(); int ret = 0; //固定B，A依次增加 for (int i = 0; i < n; i++) { int len = min(m, n - i); int maxlen = maxLength(A, B, i, 0, len); ret = max(ret, maxlen); } //固定A，B依次增加 for (int i = 0; i < m; i++) { int len = min(n, m - i); int maxlen = maxLength(A, B, 0, i, len); ret = max(ret, maxlen); } return ret; } };

最长公共子序列

• 1143 最长公共子序列(LCS)

• 给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ，返回 0 。

  一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

  例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。 两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。

  • 思路：维护一个二维dp[i][j]数组，其定义是：text1的第i个字符和text2的第j个字符的最大公共子序列长度。

  • 推出递推公式

  • 1 2 3 4 5 6 7 8 9 10 11 12

    if(text1[i]==text2[j]){ dp[i][j]=dp[i-1][j-1]+1; } dp[i][j]=max(dp[i][j],max(dp[i-1][j],dp[i][j-1])); //实际上更简单的是 if(text[i]==text2[j]){ dp[i][j]=dp[i-1][j-1]+1 }else{ dp[i][j]=max(dp[i-1][j],dp[i][j-1]); }

  • 然后初始化第一行第一列即可

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39

  class Solution { public: int longestCommonSubsequence(string text1, string text2) { int n1=text1.size();//row int n2=text2.size();//col vector<vector<int>> dp(n1,vector<int>(n2,0)); //初始化第一行 if(text1[0]==text2[0]){ dp[0][0]=1; } for(int i=1;i<n2;++i){ if(text2[i]==text1[0]) dp[0][i]=max(dp[0][i]+1,dp[0][i-1]); else{ dp[0][i]=dp[0][i-1]; } } //初始化第一列 for(int i=1;i<n1;++i){ if(text1[i]==text2[0]) dp[i][0]=max(dp[i][0]+1,dp[i-1][0]); else{ dp[i][0]=dp[i-1][0]; } } //状态转移 for(int i=1;i<n1;++i){ for(int j=1;j<n2;++j){ if(text1[i]==text2[j]){ dp[i][j]=dp[i-1][j-1]+1; } dp[i][j]=max(dp[i][j],max(dp[i-1][j],dp[i][j-1])); } } return dp[n1-1][n2-1]; } };

• 最长公共子串（连续）

  • 给定两个字符串str1和str2,输出两个字符串的最长公共子串。

    例如 abceef 和a2b2cee3f的最长公共子串就是cee。公共子串是两个串中最长连续的相同部分。

    如何分析呢? 和上面最长公共子序列的分析方式相似，要进行动态规划匹配，并且逻辑上处理更简单，只要当前i,j不匹配那么dp值就为0，如果可以匹配那么就变成dp[i-1][j-1] + 1

    核心的状态转移方程为：

    1 2	dp[i][j] = dp[i-1][j-1] + 1 //text1[i]==text2[j]时 dp[i][j] = 0 //text1[i]!=text2[j]时

• 583. 两个字符串的删除操作

  给定两个单词 word1 和 word2，找到使得 word1 和 word2 相同所需的最小步数，每步可以删除任意一个字符串中的一个字符。

  • 思路：最长公共子序列的变种问题，求出最长公共子序列，长度和减去两倍的子序列长度即为输出结果。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34

  class Solution { public: int minDistance(string word1, string word2) { int rows=word2.size(); int cols=word1.size(); vector<vector<int>> dp(rows,vector<int>(cols,0)); if(word1[0]==word2[0]){ dp[0][0]=1; } //初始化 for(int j=1;j<cols;++j){ dp[0][j]=dp[0][j-1]; if(word2[0]==word1[j]){ dp[0][j]=1; } } for(int i=1;i<rows;++i){ dp[i][0]=dp[i-1][0]; if(word2[i]==word1[0]){ dp[i][0]=1; } } for(int i=1;i<rows;++i){ for(int j=1;j<cols;++j){ if(word2[i]==word1[j]){ dp[i][j]=dp[i-1][j-1]+1; } dp[i][j]=max(dp[i][j],max(dp[i-1][j],dp[i][j-1])); } } return rows+cols-2*dp[rows-1][cols-1]; } };

• 72. 编辑距离

  给你两个单词 word1 和 word2，请你计算出将 word1 转换成 word2 所使用的最少操作数 。

  你可以对一个单词进行如下三种操作：

  • 插入一个字符
  • 删除一个字符
  • 替换一个字符

  思路：可插入、可删除、可替换，表面上看，对于两个单词来说，一共有六个操作：

  • 插入word1
  • 插入word2
  • 删除word1
  • 删除word2
  • 替换word1
  • 替换word2

  然而实际上只有三种操作：插入word1，插入word2，替换word1/word2。仔细想想，插入word1其实和删除word2是一样的。这里我们从没有字符串开始动规，即初始化都没有字符串。

  

  

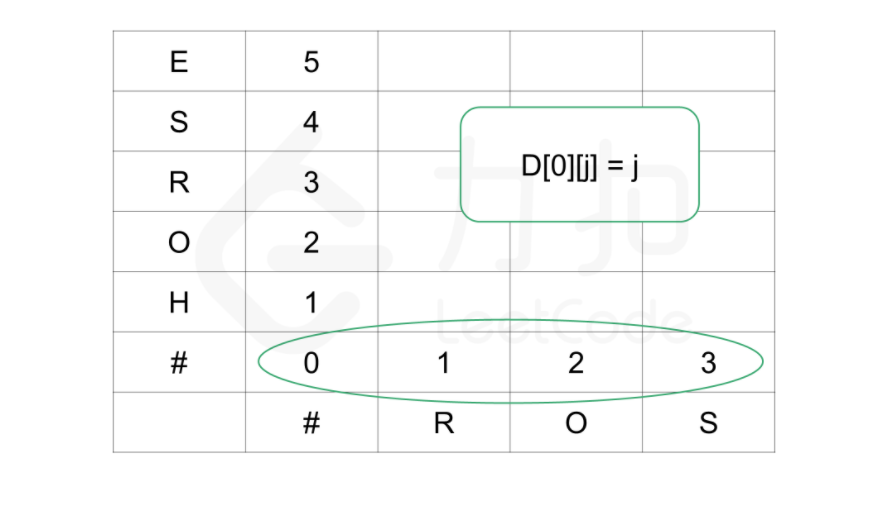
  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27

  class Solution { public: int minDistance(string word1, string word2) { int rows=word2.size(); int cols=word1.size(); vector<vector<int>> dp(rows+1,vector<int>(cols+1,0)); //初始化第一行 for(int j=1;j<cols+1;++j){ dp[0][j]=j; } //初始化第一列 for(int i=1;i<rows+1;++i){ dp[i][0]=i; } //动规 for(int i=1;i<rows+1;++i){ for(int j=1;j<cols+1;++j){ if(word1[j-1]==word2[i-1]){ dp[i][j]=min(dp[i-1][j]+1,min(dp[i][j-1]+1,dp[i-1][j-1])); }else{ dp[i][j]=min(dp[i-1][j]+1,min(dp[i][j-1]+1,dp[i-1][j-1]+1)); } } } return dp[rows][cols]; } };

不同子序列

• 这题是 0-1背包滚动数组的变种问题。

• 不同子序列

  • 先看一个开胃的问题——有多少个pat

  • 1 2 3 4 5 6 7 8 9 10 11

    int len = s.length(), result = 0, countp = 0, countt = 0; for (int i = 0; i < len; i++) { if (s[i] == 'T') countt++; } for (int i = 0; i < len; i++) { if (s[i] == 'P') countp++; if (s[i] == 'T') countt--; if (s[i] == 'A') result = (result + (countp * countt) % 1000000007) % 1000000007; } cout << result;

  • 思路很简单：因为只有三个字母pat，当遇到a时则一直加下去，加的数是a前面p字母的个数和后面t字母的个数的乘积。

  • 现在回头看

    • 题干：

    • 给定一个字符串 s 和一个字符串 t ，计算在 s 的子序列中 t 出现的个数。

      字符串的一个 子序列 是指，通过删除一些（也可以不删除）字符且不干扰剩余字符相对位置所组成的新字符串。（例如，"ACE" 是 "ABCDE" 的一个子序列，而 "AEC" 不是）

    • 思路：维护一个dp二维数组，初始化行和列，推出状态方程，dp的含义是t[i-1]和s[j-1]的匹配的总数，习惯上t为行数，s为列数

    • 1 2 3 4

      if(s[j-1]==t[i-1]){ dp[i][j]=dp[i][j-1]+dp[i-1][j-1];//选择位置匹配和不匹配两种，本来就有不匹配的数量，加上匹配的数量就是总的数量 }else{ dp[i][j]=dp[i][j-1];//不匹配的数量

    • 

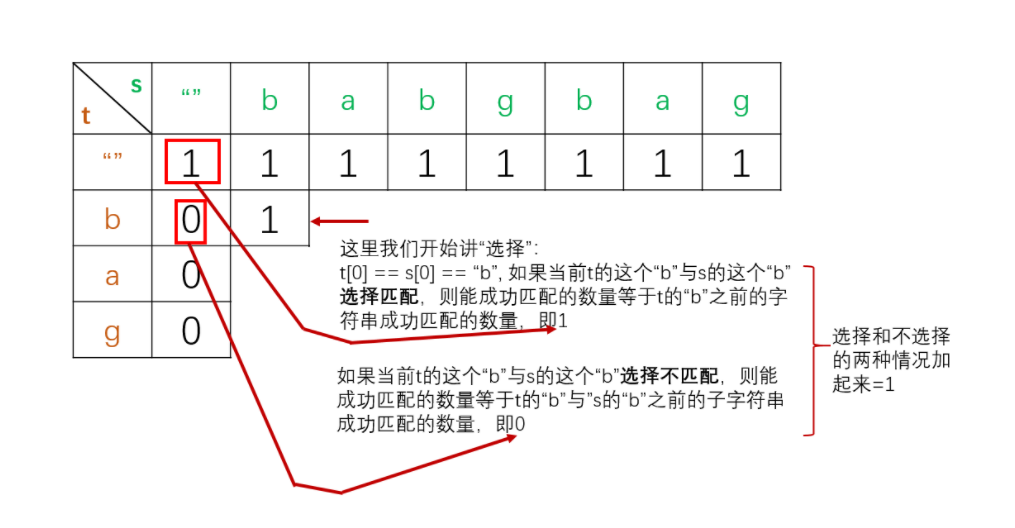
    • 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32

      class Solution { public: int numDistinct(string s, string t) { int row=t.size(); int col=s.size(); if(col<row){ return 0; } vector<vector<unsigned long long>> dp(row+1,vector<unsigned long long>(col+1,0)); //初始化第一行, for(int i=0;i<col+1;++i){ dp[0][i]=1; } //初始化第一列 for(int i=1;i<row+1;++i){ dp[i][0]=0; } //状态转移 for(int i=1;i<row+1;++i){ for(int j=1;j<col+1;++j){ if(s[j-1]==t[i-1]){ dp[i][j]=dp[i][j-1]+dp[i-1][j-1]; }else{ dp[i][j]=dp[i][j-1]; } } } return dp[row][col]; } };

    • 降维优化后的dp解法

      1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

      class Solution { public: int numDistinct(string s, string t) { vector<unsigned long long> dp(t.size()+1);//1-size才是对于的t字符串 dp[0]=1;//初始化叠加 for(int i=0;i<s.size();i++) { //注意一定是t从后往前遍历，防止前面造成干扰 for(int j=t.size()-1;j>=0;j--) { if(t[j]==s[i])//否则dp[j+1]不变 { dp[j+1]=dp[j+1]+dp[j];//可选择匹配或不匹配的相加 } } } return dp[t.size()]; } };

• 青蛙跳台

  • 1 2 3 4 5 6

    剑指 Offer 10- II. 青蛙跳台阶问题 一只青蛙一次可以跳上1级台阶，也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。 答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。 /*类似斐波那契数列，最后一步要么一步，要么两步，只是初始化不一样 fn=fn-1+fn-2

  • 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31

    class Solution { public: //首先明确，如何递推 int numWays(int n) { if(n==0){ return 1; } vector<long long> dp(n+1,0); dp[0]=1; dp[1]=1; for(int i=2;i<=n;++i){ dp[i]=dp[i-1]%1000000007+dp[i-2]%1000000007; } return dp[n]%1000000007; } }; //以下是标答——节省时间的同时也节省空间 class Solution { public: int numWays(int n) { int a = 1, b = 1, sum; for(int i = 0; i < n; i++){ sum = (a + b) % 1000000007; a = b; b = sum; } return a; } };

• 斐波那契数列

  • 1 2 3 4 5 6 7 8

    剑指 Offer 10- I. 斐波那契数列 写一个函数，输入 n ，求斐波那契（Fibonacci）数列的第 n 项（即 F(N)）。斐波那契数列的定义如下： F(0) = 0,   F(1) = 1 F(N) = F(N - 1) + F(N - 2), 其中 N > 1. 斐波那契数列由 0 和 1 开始，之后的斐波那契数就是由之前的两数相加而得出。 答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

  • 1 2 3 4 5 6 7 8 9 10 11 12 13 14

    class Solution { public: int fib(int n) { if(n==0){return 0;} if(n==1){return 1;} vector<long long> dp(n+1,0); dp[0]=0;dp[1]=1; for(int i=2;i<=n;++i){ dp[i]=dp[i-1]%1000000007+dp[i-2]%1000000007; } return dp[n]%1000000007; } };

• 剑指 Offer 19. 正则表达式匹配

  1	请实现一个函数用来匹配包含'. '和'*'的正则表达式。模式中的字符'.'表示任意一个字符，而'*'表示它前面的字符可以出现任意次（含0次）。在本题中，匹配是指字符串的所有字符匹配整个模式。例如，字符串"aaa"与模式"a.a"和"ab*ac*a"匹配，但与"aa.a"和"ab*a"均不匹配。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

  /* 思路：： p是pattern为列数，s是string为行数 状态定义： 设动态规划矩阵 dp ， dp[i][j] 代表字符串 s 的前 i-1 个字符和 p 的前 j-1 个字符能否匹配。 转移方程： 需要注意，由于 dp[0][0] 代表的是空字符的状态， 因此 dp[i][j] 对应的添加字符是 s[i - 1] 和 p[j - 1] 。 当 p[j - 1] = '*' 时， dp[i][j] 在当以下三种任一情况为 truetrue 时等于 truetrue ： 1.dp[i][j - 2]： 即将字符组合 p[j - 2] * 看作出现 0 次时，能否匹配； 2.dp[i - 1][j] 且 s[i - 1] = p[j - 2]: 即让字符 p[j - 2] 多出现 1 次时，能否匹配； 3.dp[i - 1][j] 且 p[j - 2] = '.': 即让字符 '.' 多出现 1 次时，能否匹配； 当 p[j - 1] != '*' 时， dp[i][j] 在当以下两种任一情况为 truetrue 时等于 truetrue ： 1.dp[i - 1][j - 1] 且 s[i - 1] = p[j - 1]： 即让字符 p[j - 1] 多出现一次时，能否匹配； 2.dp[i - 1][j - 1] 且 p[j - 1] = '.'： 即将字符 . 看作字符 s[i - 1] 时，能否匹配； dp矩阵初始化： 需要先初始化 dp 矩阵首行，以避免状态转移时索引越界。 1.dp[0][0] = true： 代表两个空字符串能够匹配。 2.dp[0][j] = dp[0][j - 2] 且 p[j - 1] = '*'： 首行 s 为空字符串，因此当 p 的偶数位为 * 时才能够匹配（即让 p 的奇数位出现 0 次，保持 p 是空字符串）。因此，循环遍历字符串 p ，步长为 2（即只看偶数位）。 函数返回值： dp 矩阵右下角字符，代表字符串 s 和 p 能否匹配 */

• 

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43

  class Solution { public: bool isMatch(string s, string p) { int m=s.size()+1; int n=p.size()+1;//m行n列,注意加一 vector<vector<bool>> dp(m,vector<bool>(n,false)); //初始化首行 dp[0][0]=true; for(int i=2;i<n;i+=2){ if(dp[0][i-2] && p[i-1]=='*'){ dp[0][i]=true; } } //依次判断,从1,1开始 for(int i=1;i<m;++i){ for(int j=1;j<n;++j){ //不等于*,两种情况 if(p[j-1]!='*'){ if(dp[i-1][j-1]&& s[i-1]==p[j-1]){ dp[i][j]=true; } else if(dp[i-1][j-1]&& p[j-1]=='.'){ dp[i][j]=true; } } //等于分三种情况 else if(p[j-1]=='*'){ if(dp[i][j-2]){ dp[i][j]=true;//*号使得p[j-2]出现0次，但只要p[j-3]匹配即可 }else if(dp[i-1][j] && p[j-2]=='.'){ dp[i][j]=true;//重复"." }else if(dp[i-1][j] && p[j-2]==s[i-1]){ dp[i][j]=true;//重复p[j-2] } } } } return dp[m-1][n-1]; } };

• 连续子数组的最大和

• 剑指 Offer 42. 连续子数组的最大和

  输入一个整型数组，数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。

  要求时间复杂度为O(n)。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

  //dp[i]= dp[i-1]+num[i](dp[i-1]>0) // nums[i] //或者dp[i] = max(dp[i - 1] + nums[i], nums[i]);也可以，最后输出dp数组的最大值即可 class Solution { public: int maxSubArray(vector<int>& nums) { int ret=nums[0]; int n=nums.size(); //直接原数组改，或者另开也行，另开最后去max，或者直接得到max for(int i=1;i<n;++i){ if(nums[i-1]>0){ nums[i]=nums[i]+nums[i-1]; } //取最大值 if(nums[i]>ret){ ret=nums[i]; } } return ret; } };

零钱兑换

• 322. 零钱兑换

  给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。

  计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额，返回 -1 。

  你可以认为每种硬币的数量是无限的。

  • 解法一：

  • 

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21

  //转化为背包问题 class Solution { public: int coinChange(vector<int>& coins, int amount) { int n=coins.size(); vector<int> dp(amount+1,0); for(int i=1;i<=amount;++i){ dp[i]=INT_MAX; for(int j=0;j<n;++j){ //一定要加dp[i-coins[j]]>=0，不然无法判断之前的能否放下物品，不能放下是-1 if(i-coins[j]>=0 && dp[i-coins[j]]>=0 ){ dp[i]=min(dp[i],dp[i-coins[j]]+1); } } if(dp[i]==INT_MAX){ dp[i]=-1; } } return dp[amount]; } };

  • 思路二：完全背包问题，和下面的零钱兑换2类似

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36

  class Solution { public: int coinChange(vector<int>& coins, int amount) { if(amount==0){ return 0; } int n=coins.size(); sort(coins.begin(),coins.end());//从小到大排序 vector<vector<int>> dp(n,vector<int>(amount+1,-1)); for(int i=1;i<=amount;++i){ if(i%coins[0]==0){ dp[0][i]=i/coins[0]; } } for(int j=1;j<n;++j){ dp[j][0]=0; } for(int i=1;i<n;++i){ for(int j=1;j<=amount;++j){ dp[i][j]=INT_MAX; //选择放还是不放。选最小的 if(dp[i-1][j]>0){ dp[i][j]=dp[i-1][j]; } if(j>=coins[i] && dp[i][j-coins[i]]>=0){ dp[i][j]=min(dp[i][j],dp[i][j-coins[i]]+1); } if(dp[i][j]==INT_MAX){ dp[i][j]=-1; } } } return dp[n-1][amount]; } };

• 518. 零钱兑换 II

  给你一个整数数组 coins 表示不同面额的硬币，另给一个整数 amount 表示总金额。

  请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额，返回 0 。

  假设每一种面额的硬币有无限个。

• 思路：用

  $$ \textit{dp}[x] $$ 表示金额之和等于 x的最大硬币组合数
  • 这个条件告诉我们用动态规划
  • 因为回溯法更用于返回所有组合，而不单单是组合数，复杂度较高

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14

  class Solution { public: int change(int amount, vector<int>& coins) { vector<int> ret(amount+1,0);//0 1 2 3...块钱的分配，dp数组，自底向上 ret[0]=1; //依次取一个硬币,保证不会重复，112和211是一样的，和青蛙跳阶梯不一样 for(auto &coin:coins){ for(int i=coin;i<=amount;++i){ ret[i]=ret[i]+ret[i-coin]; } } return ret[amount]; } };

• 思路二：转换为背包问题（更易于理解）

• 有一个背包，最大容量为 amount，有一系列物品 coins，每个物品的重量为 coins[i]，每个物品的数量无限。请问有多少种方法，能够把背包恰好装满？

  第一步要明确两点，「状态」和「选择」，状态有两个，就是「背包的容量」和「可选择的物品」，选择就是「装进背包」或者「不装进背包」。

  dp[i][j] 的定义：若只使用前 i 个物品（可以重复使用），当背包容量为 j 时，有 dp[i][j] 种方法可以装满背包。

  最终想得到的答案是 dp[N][amount]，其中 N 为 coins 数组的大小。

  如果你不把这第 i 个物品装入背包，也就是说你不使用 coins[i] 这个面值的硬币，那么凑出面额 j 的方法数 dp[i][j] 应该等于 dp[i-1][j]，继承之前的结果。

  如果你把这第 i 个物品装入了背包，也就是说你使用 coins[i-1] 这个面值的硬币，那么 dp[i][j] 应该等于 dp[i][j-coins[i-1]]。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26

  class Solution { public: int change(int amount, vector<int>& coins) { int row=coins.size()+1; int col=amount+1; vector<vector<int>> dp(row,vector<int>(col,0)); //初始化 for(int i=0;i<row;++i){ dp[i][0]=1; } //递推方程 for(int i=1;i<row;++i){ for(int j=1;j<col;++j){ if(j-coins[i-1]>=0){ //选择放改硬币还是不放,所以相加 dp[i][j]=dp[i-1][j]+dp[i][j-coins[i-1]]; }else{ dp[i][j]=dp[i-1][j]; } } } return dp[row-1][col-1]; } };

• 300 最长递增子序列——还有二分查找+贪心的思路，复杂度更低

  • 给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

    子序列是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26

  /* dp 数组的定义：dp[i] 表示以 nums[i] 这个数结尾的最长递增子序列的长度。 那么 dp 数组中最大的那个值就是最长的递增子序列长度。 */ class Solution { public: int lengthOfLIS(vector<int>& nums) { if(nums.size()==0){ return 0; } vector<int> dp(nums.size(),1); int ret=1;//保证一个元素也可以返回 for(int i=1;i<nums.size();++i){ for(int j=0;j<i;++j){ //严格递增，没有等号 if(nums[j]<nums[i]){ dp[i]=max(dp[i],dp[j]+1); } } if(ret<dp[i]){ ret=dp[i]; } } return ret; } };

• 256. 粉刷房子

  假如有一排房子，共 n 个，每个房子可以被粉刷成红色、蓝色或者绿色这三种颜色中的一种，你需要粉刷所有的房子并且使其相邻的两个房子颜色不能相同。

  当然，因为市场上不同颜色油漆的价格不同，所以房子粉刷成不同颜色的花费成本也是不同的。每个房子粉刷成不同颜色的花费是以一个 n x 3 的正整数矩阵 costs 来表示的。

  例如，costs[0][0] 表示第 0 号房子粉刷成红色的成本花费；costs[1][2] 表示第 1 号房子粉刷成绿色的花费，以此类推。

  请计算出粉刷完所有房子最少的花费成本。

  

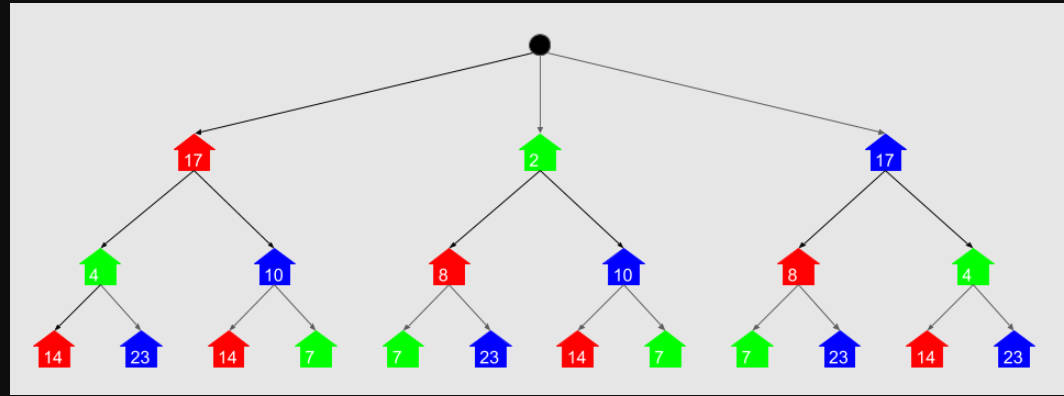
• 1 2 3 4 5 6 7 8 9 10 11 12 13

  class Solution { public: int minCost(vector<vector<int>>& costs) { //动态规划，直接在原数组上改，就不会有重复子问题了 int n=costs.size(); for(int i=n-2;i>=0;--i){ costs[i][0]+=min(costs[i+1][1],costs[i+1][2]); costs[i][1]+=min(costs[i+1][0],costs[i+1][2]); costs[i][2]+=min(costs[i+1][1],costs[i+1][0]); } return min(min(costs[0][0],costs[0][1]),costs[0][2]); } };

• 265. 粉刷房子 II

• 假如有一排房子，共 n 个，每个房子可以被粉刷成 k 种颜色中的一种，你需要粉刷所有的房子并且使其相邻的两个房子颜色不能相同。

  当然，因为市场上不同颜色油漆的价格不同，所以房子粉刷成不同颜色的花费成本也是不同的。每个房子粉刷成不同颜色的花费是以一个 n x k 的矩阵来表示的。

  例如，costs[0][0] 表示第 0 号房子粉刷成 0 号颜色的成本花费；costs[1][2] 表示第 1 号房子粉刷成 2 号颜色的成本花费，以此类推。请你计算出粉刷完所有房子最少的花费成本。

  注意：

  所有花费均为正整数。

• 思路同上，只是多了一个判读首尾然后返回最小值的操作

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23

  class Solution { public: int minCostII(vector<vector<int>>& costs) { int n=costs.size(); int k=costs[0].size(); for(int i=n-2;i>=0;--i){ for(int j=0;j<k;++j){ int temp; if(j==0){ temp=*min_element(costs[i+1].begin()+1, costs[i+1].end()); }else if(j==k-1){ temp=*min_element(costs[i+1].begin(), costs[i+1].end()-1); }else{ temp=min(*min_element(costs[i+1].begin(),costs[i+1].begin()+j), *min_element(costs[i+1].begin()+j+1,costs[i+1].end())); } costs[i][j]+=temp; } } return *min_element(costs[0].begin(), costs[0].end()); } };

• 1035. 不相交的线

• • 题干：在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。

    现在，可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线，这些直线需要同时满足满足：

    nums1[i] == nums2[j] 且绘制的直线不与任何其他连线（非水平线）相交。 请注意，连线即使在端点也不能相交：每个数字只能属于一条连线。

    以这种方法绘制线条，并返回可以绘制的最大连线数。

  • 思路：两个数组相等的数连线不想交，可以转换为最长公共子序列，不改变先后顺序

  • 转换思路就很简单了。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28

  class Solution { public: int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) { //转换思路，即求解最长公共子序列的长度 int n1=nums1.size()+1; int n2=nums2.size()+1; vector<vector<int>> dp(n1,vector<int>(n2,0)); //初始化 // for(int i=0;i<n2;++i){ // dp[0][i]=0; // } // for(int i=0;i<n1;++i){ // dp[i][0]=0; // } //状态转移 for(int i=1;i<n1;++i){ for(int j=1;j<n2;++j){ //以下递推公式可以化简，见之前的题目 if(nums1[i-1]==nums2[j-1]){ dp[i][j]=dp[i-1][j-1]+1; } dp[i][j]=max(dp[i][j],max(dp[i-1][j],dp[i][j-1])); } } return dp[n1-1][n2-1]; } };

• 712. 两个字符串的最小ASCII删除和

  给定两个字符串s1, s2，找到使两个字符串相等所需删除字符的ASCII值的最小和。

  • 最长公共子序列的变种问题

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27

  class Solution { public: int minimumDeleteSum(string s1, string s2) { //转换思路：求解最长公共ascii码的数值和，最后相减即可 int n1=s1.size()+1; int n2=s2.size()+1; if(n1==1&&n2==1){ return 0; } long long sum=0; vector<vector<int>> dp(n1,vector<int>(n2,0)); for(int i=1;i<n1;++i){ sum+=s1[i-1]; for(int j=1;j<n2;++j){ if(s1[i-1]==s2[j-1]){ dp[i][j]=dp[i-1][j-1]+s1[i-1]; }else{ dp[i][j]=max(dp[i-1][j],dp[i][j-1]); } } } for(int i=1;i<n2;++i){ sum+=s2[i-1]; } return sum-dp[n1-1][n2-1]*2;//注意乘2 } };

买卖股票

• 121. 买卖股票的最佳时机

  给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

  你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

  返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

• 思路1：暴力，固定一个数，判读右边的最大值，两者相减，时间复杂度O(n^2)。

• 思路2：遍历一遍，取差值，差值小于0，重新开始；大于等于零，继续加

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

  class Solution { public: int maxProfit(vector<int>& prices) { int n = prices.size(); vector<int> now(n,0); for(int i =1;i<n;++i){ now[i]=prices[i]-prices[i-1]; } int last=0; int ret = 0; for(int i =1;i<n;++i){ if(last+now[i]<0){ last =0; continue; }else{ last+=now[i]; ret =max(ret,last); } } return ret; } };

背包问题

• 背包九讲——掌握01背包和完全背包即可，其他笔试不太常见
• 切钢条、分蛋糕是简化版的背包问题

0-1背包（二维数组）

• 有N件物品和一个最多能背重量为W 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

• 每一件物品其实只有两个状态，取或者不取，所以可以使用回溯法搜索出所有的情况，那么时间复杂度就是O(2^n)，这里的n表示物品数量。二叉树的遍历。

  所以暴力的解法是指数级别的时间复杂度。进而才需要动态规划的解法来进行优化！

• 思路

  • 

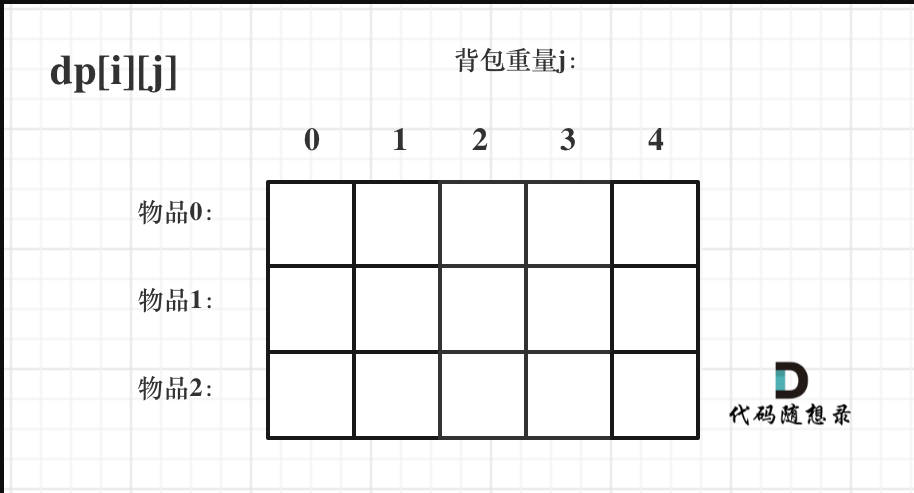
  • 1 2 3 4 5 6 7 8 9 10 11 12

    /* dp[i][j]的含义：从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。 那么可以有两个方向推出来dp[i][j]， 不放物品i：由dp[i - 1][j]推出，即背包容量为j，里面不放物品i的最大价值，此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量时，物品i无法放进背包中，所以被背包内的价值依然和前面相同。) 放物品i：由dp[i - 1][j - weight[i]]推出，dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值，那么dp[i - 1][j - weight[i]] + value[i] （物品i的价值），就是背包放物品i得到的最大价值 所以递归公式： dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 因为物品只有一个，所以只能从上一层往下走 */

  • 初始化第一行和第一列

    

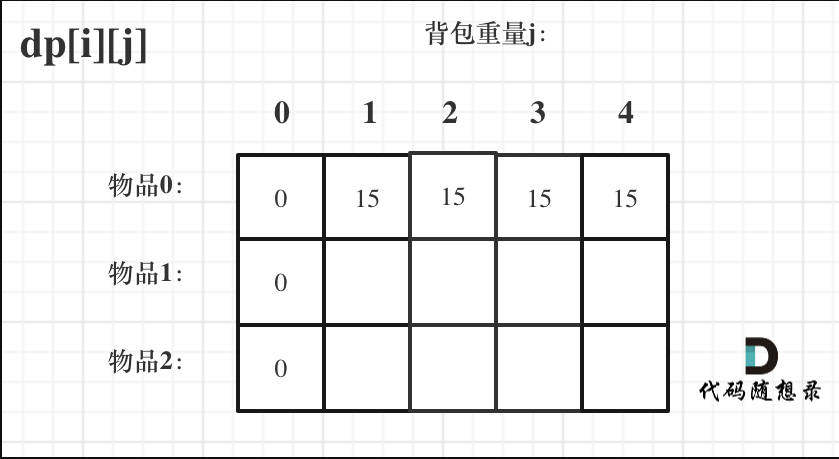
  • 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

    // 初始化 dp vector<vector<int>> dp(weight.size(), vector<int>(bagWeight + 1, 0));//全部初始化为0了 //初始化第一行 for (int j = weight[0]; j <= bagWeight; j++) { dp[0][j] = value[0]; } // weight数组的大小 就是物品个数 for(int i = 1; i < weight.size(); i++) { // 遍历物品 for(int j = 1; j <= bagWeight; j++) { // 遍历背包容量 if (j < weight[i]) dp[i][j] = dp[i - 1][j]; else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); } }

0-1背包（滚动数组）

• 思想：

  1 2 3 4 5 6 7 8 9 10 11

  /* 对于背包问题其实状态都是可以压缩的。 在使用二维数组的时候，递推公式：dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 其实可以发现如果把dp[i - 1]那一层拷贝到dp[i]上，表达式完全可以是：dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]); 与其把dp[i - 1]这一层拷贝到dp[i]上，不如只用一个一维数组了，只用dp[j]（一维数组，也可以理解是一个滚动数组）。 这就是滚动数组的由来，需要满足的条件是上一层可以重复利用，直接拷贝到当前层。 */

• 1 2 3 4 5

  for(int i = 0; i < weight.size(); i++) { // 遍历物品 for(int j = bagWeight; j >= weight[i]; j--) { // 倒序遍历背包容量 dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); } }

  这里大家发现和二维dp的写法中，遍历背包的顺序是不一样的！

  二维dp遍历的时候，背包容量是从小到大，而一维dp遍历的时候，背包是从大到小。

  为什么呢？

  倒叙遍历是为了保证物品i只被放入一次！。因为如果一旦正序遍历了，那么物品0就会被重复加入多次！但是物品只有一个！！！

  举一个例子：物品0的重量weight[0] = 1，价值value[0] = 15

  如果正序遍历

  dp[1] = dp[1 - weight[0]] + value[0] = 15

  dp[2] = dp[2 - weight[0]] + value[0] = 30

  此时dp[2]就已经是30了，意味着物品0，被放入了两次，所以不能正序遍历。

  为什么倒叙遍历，就可以保证物品只放入一次呢？

  倒叙就是先算dp[2]

  dp[2] = dp[2 - weight[0]] + value[0] = 15 （dp数组已经都初始化为0）

  dp[1] = dp[1 - weight[0]] + value[0] = 15

  所以从后往前循环，每次取得状态不会和之前取得状态重合，这样每种物品就只取一次了。

  那么问题又来了，为什么二维dp数组历的时候不用倒叙呢？

  因为对于二维dp，dp[i][j]都是通过上一层即dp[i - 1][j]计算而来，本层的dp[i][j]并不会被覆盖！

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

  void test_1_wei_bag_problem() { vector<int> weight = {1, 3, 4}; vector<int> value = {15, 20, 30}; int bagWeight = 4; // 初始化 vector<int> dp(bagWeight + 1, 0); for(int i = 0; i < weight.size(); i++) { // 遍历物品 for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量 dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); } } cout << dp[bagWeight] << endl; } int main() { test_1_wei_bag_problem(); }

• 416. 分割等和子集

  给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

  • 思路1：回溯法——超时，类似第40题组合总和二。

    1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31

    class Solution { public: vector<int> path; bool check(vector<int>& nums,int n, int begin,long long sum, long long target){ if(path.size()==n){ return false; } if(sum == target){ return true; } if(sum > target){ return false; } bool ret = false; for (int i=begin;i<n;++i){ if(i>begin && nums[i-1]==nums[i]){ continue; } sum+=nums[i]; path.push_back(nums[i]); ret=ret||check(nums,n,i+1,sum,target); //回溯 sum-=nums[i]; path.pop_back(); } return ret; }; };

  • 思路2：动态规划。0-1背包的变异。dp[i][j] 的定义：num前[i+1]个数能否满足j容量的背包，布尔类型。

    1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37

    class Solution { public: bool canPartition(vector<int>& nums) { sort(nums.begin(),nums.end()); int n=nums.size(); long long sum=0; for(int i=0;i<n;++i){ sum+=nums[i]; } if(sum%2!=0){ return false; } int col=sum/2; vector<vector<bool>> dp(n,vector<bool>(col+1,false)); //初始化第一列 for(int i=0;i<n;++i){ dp[i][0]=true; } //初始化第一列 if(nums[0]<=col){ dp[0][nums[0]]=true; } for(int i=1;i<n;++i){ for(int j=1;j<=col;++j){ if(j>=nums[i]){ //装入或不装入背包 dp[i][j] =dp[i-1][j]||dp[i-1][j-nums[i]]; }else{ //不装入 dp[i][j]=dp[i-1][j]; } } } return dp[n-1][col]; } };

  • 滚动数组：一定要注意，哪个是背包，哪个是物品。

  • 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32

    class Solution { public: bool canPartition(vector<int>& nums) { int sum = accumulate(nums.begin(), nums.end(), 0); if(sum%2!=0){ return false; } vector<bool> dp(sum/2+1,false); dp[0] = true; int len = sum/2; for(int &i:nums){ if(i>len){ continue; }else if(i==len){ return true; }else{ for(int j = len;j>=i;--j){ //如果前面可以计算到这个和，就不用计算了 if(dp[j]){ continue; } dp[j] = dp[j-i]; } if(dp[len]){ return true; } } } return false; } };

​

• 494. 目标和

  给你一个整数数组 nums 和一个整数 target 。

  向数组中的每个整数前添加 '+' 或 '-' ，然后串联起所有整数，可以构造一个 表达式 ：

  • 例如，nums = [2, 1] ，可以在 2 之前添加 '+' ，在 1 之前添加 '-' ，然后串联起来得到表达式 "+2-1" 。

  返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。

  • 思路1：回溯法

    1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

    class Solution { public: //不一样的回溯，更简单 int count=0; void back_tracking(vector<int>& nums,int index, int sum, int target){ if(index==nums.size()){ if(sum==target){ ++count; return; }else{ return; } } back_tracking(nums, index+1, sum+nums[index], target); back_tracking(nums, index+1, sum-nums[index], target); } int findTargetSumWays(vector<int>& nums, int target) { count=0; int sum=0; back_tracking(nums, 0, sum, target); return count; } };

  • 动态规划，转换思路，其实本质和分割等和子集 区别不大

    

    

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29

  class Solution { public: int findTargetSumWays(vector<int>& nums, int target) { int n=nums.size(); int sum=0; for(int i=0;i<n;++i){ sum+=nums[i]; } if(sum>=target &&(sum-target)%2==0){ int ret=(sum-target)/2; vector<vector<int>> dp(n+1,vector<int>(ret+1,0)); dp[0][0]=1; for(int i=1;i<=n;++i){ //注意从0开始 for(int j=0;j<=ret;++j){ if(j<nums[i-1]){ dp[i][j]=dp[i-1][j]; }else{ dp[i][j]=dp[i-1][j]+dp[i-1][j-nums[i-1]]; } } } return dp[n][ret]; }else{ return 0; } } };

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27

  //dp定义，dp[j] 表示nums的数组成的和等于j的个数，滚动数组 class Solution { public: int findTargetSumWays(vector<int>& nums, int target) { int n = nums.size(); int sum = accumulate(nums.begin(), nums.end(),0); int left = sum+target; if(abs(target)>sum){ return false; } if(left%2!=0){ return false; } left = left/2; vector<int> dp(left+1,0); dp[0] = 1; for(int &i:nums){ if(i>left){ continue; } for(int j = left;j>=i;--j){ dp[j] += dp[j-i]; } } return dp[left]; } };

完全背包

• 有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品都有无限个（也就是可以放入背包多次），求解将哪些物品装入背包里物品价值总和最大。

  完全背包和01背包问题唯一不同的地方就是，每种物品有无限件。

• 我们知道01背包内嵌的循环是从大到小遍历，为了保证每个物品仅被添加一次。

  而完全背包的物品是可以添加多次的，所以要从小到大去遍历，即：（使用滚动数组即可完成）。不需要使用二维数组，因为这个二维数组并不涉及上一层的数，二维第一行的初始化还麻烦一点。

  1 2 3 4 5 6

  // 先遍历物品，再遍历背包 for(int i = 0; i < weight.size(); i++) { // 遍历物品 for(int j = weight[i]; j <= bagWeight ; j++) { // 遍历背包容量 dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); } }

• 01背包中二维dp数组的两个for遍历的先后循序是可以颠倒了，一维dp数组的两个for循环先后循序一定是先遍历物品，再遍历背包容量。

• 在完全背包中，对于一维dp数组来说，其实两个for循环嵌套顺序同样无所谓！

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

  // 先遍历物品，在遍历背包 void test_CompletePack() { vector<int> weight = {1, 3, 4}; vector<int> value = {15, 20, 30}; int bagWeight = 4; vector<int> dp(bagWeight + 1, 0); for(int i = 0; i < weight.size(); i++) { // 遍历物品 for(int j = weight[i]; j <= bagWeight; j++) { // 遍历背包容量 dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); } } cout << dp[bagWeight] << endl; } int main() { test_CompletePack(); }

打家劫舍问题

• 待补充

状压DP

• 基本思想——状态压缩成一个数字，二进制。

• 

• 

• 

• 

• 

• 一般的dp的枚举都是递归或者嵌套循环

• 

• 题目推荐

• 

树形DP

• 以上例题常见的都是一维DP数组、二维DP数组、滚动数组

• 337. 打家劫舍 III

• • 在上次打劫完一条街道之后和一圈房屋后，小偷又发现了一个新的可行窃的地区。这个地区只有一个入口，我们称之为“根”。 除了“根”之外，每栋房子有且只有一个“父“房子与之相连。一番侦察之后，聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果两个直接相连的房子在同一天晚上被打劫，房屋将自动报警。

    计算在不触动警报的情况下，小偷一晚能够盗取的最高金额。

  • 暴力法

    • 超时的问题：因为多次重复计算树枝。

    • 思路：分为

      • 偷父节点，然后加左右子树的隔两代节点

      • 不偷父节点，分别加左右子树的节点和

    • 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

      class Solution { public: int rob(TreeNode* root) { if(!root){ return 0; } if(!root->left && !root->right){ return root->val; } //偷父节点 int val1=root->val; //先左孩子 if(root->left){ val1+=rob(root->left->left)+rob(root->left->right); } //再右孩子 if(root->right){ val1+=rob(root->right->left)+rob(root->right->right); } //不偷父亲 return max(val1,rob(root->left)+rob(root->right)); } };

    • 然而这种暴力法是会超时的！！

  • 使用DP，设置两个哈希表，后序遍历

    • 注意哈希表末位不存在的话默认int返回0

    • 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27

      class Solution { public: unordered_map<TreeNode *,int> dp_rob,dp_notRob;//默认是0，所以才可 //使用后序遍历，依次返回dp值，为什么使用后序遍历，是为了当成一个备忘录，从根部一直往上，就避免了重复计算 void dfs(TreeNode *root){ if(!root){ return; } dfs(root->left); dfs(root->right); //偷父节点 dp_rob[root]=root->val+dp_notRob[root->left]+dp_notRob[root->right]; //不偷父节点，子节点可偷可不偷 dp_notRob[root]=max(dp_rob[root->left],dp_notRob[root->left])+ max(dp_rob[root->right],dp_notRob[root->right]); } int rob(TreeNode* root) { if(!root){ return 0; } dfs(root); return max(dp_rob[root],dp_notRob[root]); } };

  • 仍是DP思想，但是可以看到，后序遍历返回的每次都是两个数，所以可以直接返回一个vector值或者是pair值

    • 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

      class Solution { public: int rob(TreeNode* root) { vector<int> result = robTree(root); return max(result[0], result[1]); } // 长度为2的数组，0：不偷，1：偷 vector<int> robTree(TreeNode* cur) { if (cur == NULL) return vector<int>{0, 0}; vector<int> left = robTree(cur->left); vector<int> right = robTree(cur->right); // 偷cur int val1 = cur->val + left[0] + right[0]; // 不偷cur int val2 = max(left[0], left[1]) + max(right[0], right[1]); return {val2, val1}; } };

• 1130. 叶值的最小代价生成树

  给你一个正整数数组 arr，考虑所有满足以下条件的二叉树：

  • 每个节点都有 0 个或是 2 个子节点。
  • 数组 arr 中的值与树的中序遍历中每个叶节点的值一一对应。（知识回顾：如果一个节点有 0 个子节点，那么该节点为叶节点。）
  • 每个非叶节点的值等于其左子树和右子树中叶节点的最大值的乘积。

  在所有这样的二叉树中，返回每个非叶节点的值的最小可能总和。这个和的值是一个 32 位整数。

  1 2 3 4 5 6 7 8 9 10 11

  //例子 输入：arr = [6,2,4] 输出：32 解释： 有两种可能的树，第一种的非叶节点的总和为 36，第二种非叶节点的总和为 32。 24 24 / \ / \ 12 4 6 8 / \ / \ 6 2 2 4

  

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21

  class Solution { public: int mctFromLeafValues(vector<int>& arr) { int n=arr.size(); vector<vector<int>> dp(n,vector<int>(n,INT_MAX)); for(int i=0;i<n;++i){ dp[i][i]=0; } for(int i=n-2;i>=0;--i){ for(int j=i+1;j<n;++j){ for(int k=i;k+1<=j;++k){ dp[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]+ (*max_element(arr.begin()+i,arr.begin()+k+1)) * (*max_element(arr.begin()+k+1,arr.begin()+j+1))); } } } return dp[0][n-1]; } };

数位DP

• 按个十百千万。。数位进行dp，基础是dfs搜索，这个是套路。难点是如何dp的定义、状态的转移。
• B站参考1
• B站参考2
• 给定区间求被k整除且数位和被k整除的个数

最小化最大值问题——同二分查找

• 410. 分割数组的最大值

  给定一个非负整数数组 nums 和一个整数 m ，你需要将这个数组分成 m 个非空的连续子数组。

  设计一个算法使得这 m 个子数组各自和的最大值最小。

  • 思路：定义dp[i][j]的定义：数组的前``i个数分成j`组的和的最小的最大值。所以可以退出递推公式

  • $dp[i][j]=\min _{k>=j-1}^{i-1}{\max (dp[k][j-1], sub[i]-sub[k]))}$

  • 注意递推数组是否溢出,sub是前i个数的和

  • 

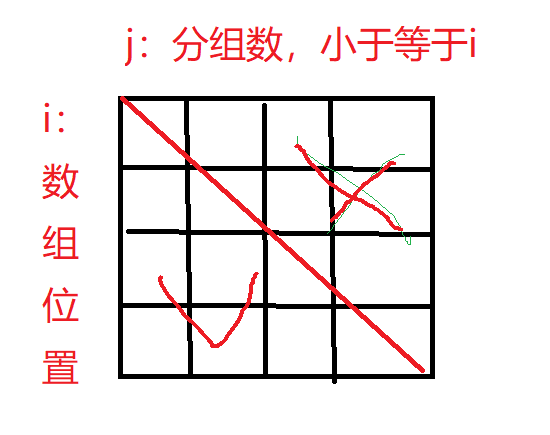
  • 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31

    class Solution { public: int splitArray(vector<int>& nums, int m) { int rows=nums.size(); vector<vector<int>> dp(rows,vector<int>(m,INT_MAX)); vector<int> sub(rows,0); sub[0]=nums[0]; int ret=sub[0]; dp[0][0]=sub[0]; //前缀和 for(int i=1;i<rows;++i){ sub[i]=sub[i-1]+nums[i]; dp[i][0]=sub[i]; ret=max(ret,nums[i]); } if(rows==m){ return ret; } //动规 for(int i=1;i<rows;++i){ for(int j=1;j<=i&&j<m;++j){ for(int k=j-1;k<=i-1;++k){ int temp=max(dp[k][j-1],sub[i]-sub[k]); dp[i][j]=min(dp[i][j],temp); } } } return dp[rows-1][m-1]; } };

股票问题

• 股票问题难点在于搞懂各种状态，有哪些状态，状态之间的相互转换。

• 714. 买卖股票的最佳时机含手续费

  给定一个整数数组 prices，其中 prices[i]表示第 i 天的股票价格 ；整数 fee 代表了交易股票的手续费用。

  你可以无限次地完成交易，但是你每笔交易都需要付手续费。如果你已经购买了一个股票，在卖出它之前你就不能再继续购买股票了。

  返回获得利润的最大值。

  注意: 这里的一笔交易指买入持有并卖出股票的整个过程，每笔交易你只需要为支付一次手续费。

  • 思路：交易当天有两个状态——当前有股票和当前没有股票。

  • 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

    class Solution { public: int maxProfit(vector<int>& prices, int fee) { //分两个状态：有股票和没有股票 int n=prices.size(); if(n==0){ return 0; } vector<vector<int>> dp(2,vector<int>(n,0)); dp[0][0]=0;//没有股票的状态 dp[1][0]=-prices[0]; for(int i=1;i<n;++i){ dp[0][i]=max(dp[0][i-1],dp[1][i-1]+prices[i]-fee);//卖出 dp[1][i]=max(dp[1][i-1],dp[0][i-1]-prices[i]);//买入 } return dp[0][n-1]; } };

• 309. 最佳买卖股票时机含冷冻期

  给定一个整数数组prices，其中第 prices[i] 表示第 *i* 天的股票价格 。

  设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票）:

  • 卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)。

  注意: 你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

  • 思路：

  • 

  • 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21

    class Solution { public: int maxProfit(vector<int>& prices) { int n=prices.size(); if(prices.empty()){ return 0; } vector<vector<int>> dp(3,vector(n,0)); //是i天之后的状态，一定要关注最大收益的定义，不然会被搞晕 dp[0][0]=-prices[0];//这天之后拥有股票的最大收益 dp[1][0]=0;//这天之后没有股票，且属于冷冻期的最大收益。卖出属于没有股票 dp[2][0]=0;//这天之后没有股票，且不处于冷冻期的最大收益 for(int i=1;i<n;++i){ dp[0][i]=max(dp[0][i-1],dp[2][i-1]-prices[i]); dp[1][i]=dp[0][i-1]+prices[i]; dp[2][i]=max(dp[2][i-1],dp[1][i-1]);//dp[1][i-1]那一天是卖出，不是冷冻期，所以也考虑这个最大收益 } return max(dp[1][n-1],dp[2][n-1]); } };

练习题

• 646. 最长数对链

  • 给出 n 个数对。 在每一个数对中，第一个数字总是比第二个数字小。

    现在，我们定义一种跟随关系，当且仅当 b < c 时，数对(c, d) 才可以跟在 (a, b) 后面。我们用这种形式来构造一个数对链。

    给定一个数对集合，找出能够形成的最长数对链的长度。你不需要用到所有的数对，你可以以任何顺序选择其中的一些数对来构造。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

  //dp的定义是以当前元素结尾的最长数对链个数 class Solution { public: int findLongestChain(vector<vector<int>>& pairs) { //先排序 int n=pairs.size(); sort(pairs.begin(),pairs.end(),[](vector<int> &a,vector<int> &b)->bool{ return a[1]<b[1]; }); vector<int> dp(n,1); dp[0]=1; int ret=1; for(int i=1;i<n;++i){ for(int j=0;j<i;++j){ if(pairs[j][1]<pairs[i][0]){ dp[i]=max(dp[i],dp[j]+1); } } ret=max(ret,dp[i]); } return ret; } };

• 368. 最大整除子集

  给你一个由 无重复 正整数组成的集合 nums ，请你找出并返回其中最大的整除子集 answer ，子集中每一元素对 (answer[i], answer[j]) 都应当满足：

  • answer[i] % answer[j] == 0 ，或
  • answer[j] % answer[i] == 0

  如果存在多个有效解子集，返回其中任何一个均可。

  • 思路：先求出最长的整除子集长度，然后定位该长度的末尾数字，同时设置一个前驱数组，记录如何返回插入。

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39

  class Solution { public: vector<int> largestDivisibleSubset(vector<int>& nums) { vector<int> ret; int n=nums.size(); if(n==0){ return ret; } vector<int> dp(n,1);//最大长度 vector<int> dp_pred(n,0);//每个数的前驱 //排序 sort(nums.begin(),nums.end()); int maxlen=1;//最大长度 int ind=0;//最大长度的最后一个数的位置 for(int i=1;i<n;++i){ for(int j=0;j<i;++j){ if(nums[i]%nums[j]==0){ if(dp[i]<dp[j]+1){ dp[i]=dp[j]+1; dp_pred[i]=j; } } } if(maxlen<dp[i]){ ind=i; maxlen=dp[i]; } } //插入数组 int i=ind; while(i>=0&&ret.size()<maxlen){ ret.push_back(nums[i]); i=dp_pred[i]; } return ret; } };

中心拓展解决回文子串

• 647. 回文子串

  给你一个字符串 s ，请你统计并返回这个字符串中 回文子串 的数目。

  回文字符串 是正着读和倒过来读一样的字符串。

  子字符串 是字符串中的由连续字符组成的一个序列。

  具有不同开始位置或结束位置的子串，即使是由相同的字符组成，也会被视作不同的子串。

  • 思路1：只是判断个数，并不需要返回所有的回文子串，所以首先应想到动态规划，而不是回溯法

    • 设DP[i][j]的定义式s[i,j]是否是一个回文串，所以返回值是方阵的右半部分值为true的个数

    • 

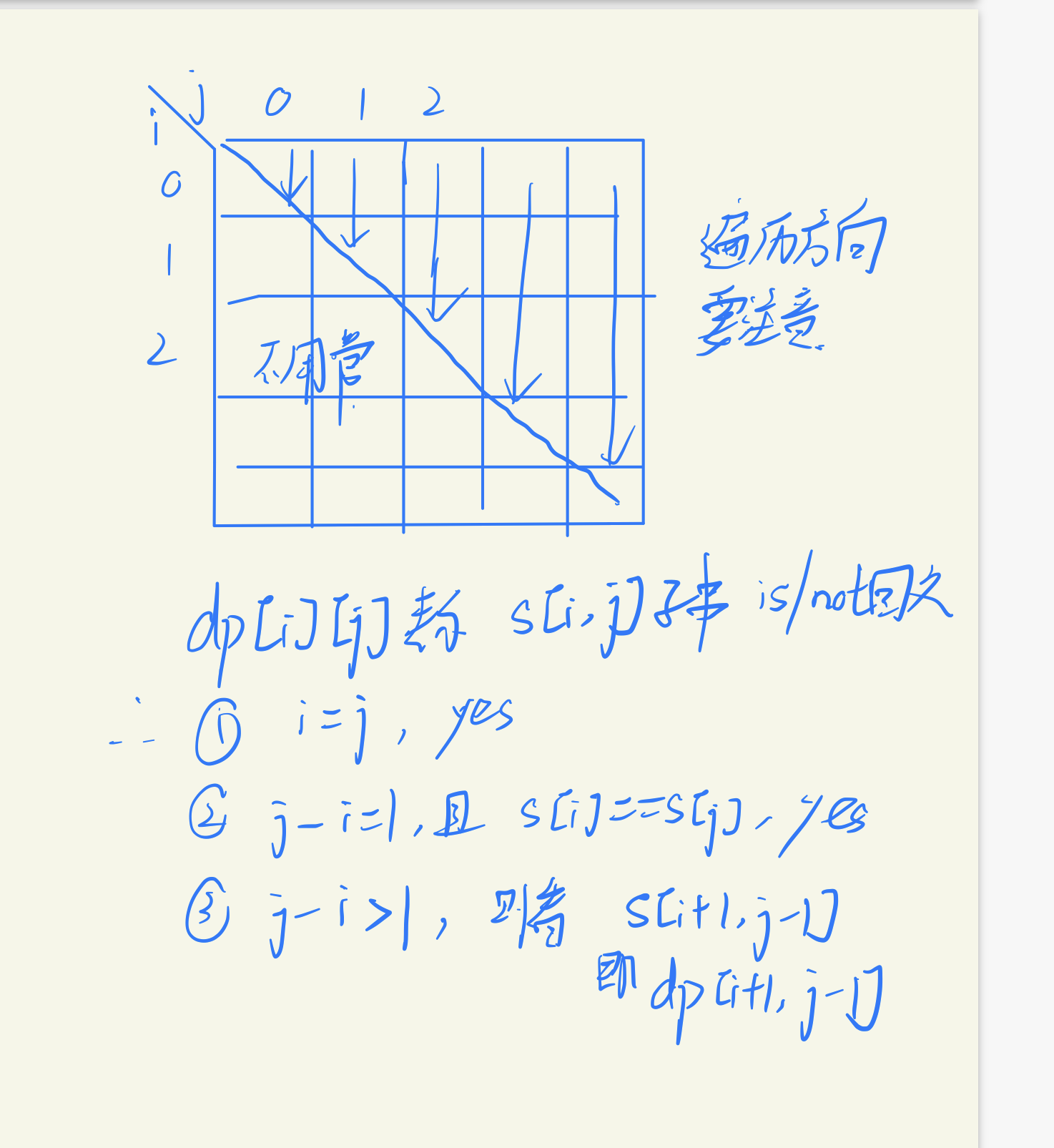
    • 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

      class Solution { public: int countSubstrings(string s) { int n=s.size(); vector<vector<bool>> dp(n,vector<bool>(n)); int ans=0; for(int j=0;j<n;++j){ for(int i=0;i<=j;++i){ if(s[i]==s[j] &&(j-i<2 || dp[i+1][j-1])){ dp[i][j]=true; ++ans; } } } return ans; } };

  • 思路二：中心拓展

    • 这是一个比较巧妙的方法，实质的思路和动态规划的思路类似。

      比如对一个字符串 ababa，选择最中间的 a 作为中心点，往两边扩散，第一次扩散发现 left 指向的是 b，right 指向的也是 b，所以是回文串，继续扩散，同理 ababa 也是回文串。

      这个是确定了一个中心点后的寻找的路径，然后我们只要寻找到所有的中心点，问题就解决了。

      中心点一共有多少个呢？看起来像是和字符串长度相等，但你会发现，如果是这样，上面的例子永远也搜不到 abab，想象一下单个字符的哪个中心点扩展可以得到这个子串？似乎不可能。所以中心点不能只有单个字符构成，还要包括两个字符，比如上面这个子串 abab，就可以有中心点 ba 扩展一次得到，所以最终的中心点由 2 * len - 1 个，分别是 len 个单字符和 len - 1 个双字符。

      如果上面看不太懂的话，还可以看看下面几个问题：

      为什么有 2 * len - 1 个中心点？

      • aba 有5个中心点，分别是 a、b、c、ab、ba abba 有7个中心点，分别是 a、b、b、a、ab、bb、ba

      什么是中心点？

      • 中心点即 left 指针和 right 指针初始化指向的地方，可能是一个也可能是两个

      为什么不可能是三个或者更多？

      • 因为 3 个可以由 1 个扩展一次得到，4 个可以由两个扩展一次得到

    1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

    class Solution { public: int countSubstrings(string s) { int n=s.size(); int len=2*n-1; int ans=0; //left=i/2,right=left+i%2;且保证right<n for(int i=0;i<len;++i){ int left=i/2; int right=left+i%2; while(left>=0 && right<n &&s[left]==s[right]){ ++ans; --left; ++right; } } return ans; } };

双重动规回文串

• 132. 分割回文串 II

  给你一个字符串 s，请你将 s 分割成一些子串，使每个子串都是回文。

  返回符合要求的 最少分割次数 。

  • 思路：首先设置dp[i][j] ,表示从i到j的子串是否是回文串，第一次动规。然后设置DP[i] ，表示从0到i的最少分割次数，第二次动规。

  • 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35

    class Solution { public: int minCut(string s) { int n=s.size(); vector<vector<int>> dp(n,vector<int>(n,0)); for(int i=0;i<n;++i){ dp[i][i]=1; } for(int i=n-2;i>=0;--i){ for(int j=i+1;j<n;++j){ if(j-i==1&&s[i]==s[j]){ dp[i][j]=1; } else if(dp[i+1][j-1]==1&&s[i]==s[j]){ dp[i][j]=1; } } } vector<int> DP(n,INT_MAX); DP[0]=0; for(int i=1;i<n;++i){ if(dp[0][i]==1){ DP[i]=0; continue; } for(int k=1;k<=i;++k){ if(dp[k][i]==1){ //s[0][k-1]和s[k][i]分成两组回文 DP[i]=min(DP[i],DP[k-1]+1); } } } return DP[n-1]; } };

• 5. 最长回文子串

  给你一个字符串 s，找到 s 中最长的回文子串。

  • 思路一：类似上一题目，使用动态规划

  • 只是需要维护一个长度还有起始位置

  • 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21

    class Solution { public: string longestPalindrome(string s) { int n=s.size(); vector<vector<bool>> dp(n,vector<bool>(n)); int len=0; int left=0; for(int j=0;j<n;++j){ for(int i=0;i<=j;++i){ if(s[i]==s[j] && (j-i<2 || dp[i+1][j-1])){ dp[i][j]=true; if((j-i+1)>len){ len=j-i+1; left=i; } } } } return s.substr(left,len); } };

  • 思路二：使用中心拓展解决

  • 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23

    class Solution { public: string longestPalindrome(string s) { int n=s.size(); int len=2*n-1; int out_len=0; int start=0; for(int i=0;i<len;++i){ int left=i/2; int right=left+i%2; while(left>=0 && right<n && s[left]==s[right]){ if(right-left+1 >out_len){ out_len=right-left+1; start=left; } --left; ++right; } } return s.substr(start,out_len); } };

• 413. 等差数列划分

  如果一个数列 至少有三个元素 ，并且任意两个相邻元素之差相同，则称该数列为等差数列。

  • 例如，[1,3,5,7,9]、[7,7,7,7] 和 [3,-1,-5,-9] 都是等差数列。

  给你一个整数数组 nums ，返回数组 nums 中所有为等差数组的 子数组 个数。

  子数组 是数组中的一个连续序列。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55

  class Solution { public: //等差子数组个数大于等于3 int numberOfArithmeticSlices(vector<int>& nums) { //解法1:双重循环,O()=n^2)，4+3+2+1等等时间复杂度是等差数列 // int n=nums.size(); // if(n<3){ // return 0; // } // int left=0; // int ret=0; // while(left<n-2){ // int right=left+1; // int reduce=nums[right]-nums[left]; // ++right; // while(right<n){ // if((nums[right]-nums[right-1])==reduce){ // ++ret; // ++right; // }else{ // break; // } // } // ++left; // } // return ret; //解法二:循环一遍直接判断，O（n） //dp的定义：当前子数组的最大长度（不是所有的最大长度，是当前差的），里面含有的子数组为n-3+1个，如1234，就有两个234 1234（注意123之前已经算了） int n=nums.size(); if(n<3){ return 0; } int d=nums[1]-nums[0]; int ret=0; vector<int> dp(n,0); dp[0]=1; dp[1]=2; for(int right=2;right<n;++right){ if(nums[right]-nums[right-1]==d){ dp[right]=dp[right-1]+1; }else{ d=nums[right]-nums[right-1]; dp[right]=2; } //判断是否是子数组 if(dp[right]>=3){ ret+=dp[right]-3+1; } } return ret; } };

• 1055. 形成字符串的最短路径

  对于任何字符串，我们可以通过删除其中一些字符（也可能不删除）来构造该字符串的子序列。

  给定源字符串 source 和目标字符串 target，找出源字符串中能通过串联形成目标字符串的子序列的最小数量。如果无法通过串联源字符串中的子序列来构造目标字符串，则返回 -1。

• 思路：使用前后判断的指针就是了，其实dp的定义式target的前i个字母可有最少组成的个数，重点的判别是否在字母之后，即check函数。同时注意src字母串有重复的，不可用哈希表。

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60

  class Solution { public: //point是上一次位置，n是src长度 bool check(string &src, char target, int &point, int n){ //已经是最大值了，所以重新开一个 if(point>=n){ point=0; } for(int i=point;i<n;++i){ if(src[i]==target){ point=i; return true; } } for(int i=0;i<point;++i){ if(src[i]==target){ point=i; return true; } } return false; } int shortestWay(string source, string target) { //初始化哈希表,前提给的源没重复字母---报错了，实际上包括重复字母 // unordered_map<char, int> help; int n=source.size(); // for(int i=0;i<n;++i){ // help[source[i]]=i; // } int m=target.size(); vector<int> dp(m,0); int pred=0;//上一次的指针 int now=0;//此次的指针 if(check(source, target[0], pred, n)){ now=pred+1;//下一个字母 dp[0]=1; }else{ return -1; } for(int i=1;i<m;++i){ if(check(source, target[i], now, n)){ if(now>pred){ dp[i]=dp[i-1]; pred=now; now=now+1; }else{ dp[i]=dp[i-1]+1; pred=now; now=now+1; } }else{ return -1; } } return dp[m-1]; } };

• 516. 最长回文子序列

  给你一个字符串 s ，找出其中最长的回文子序列，并返回该序列的长度。

  子序列定义为：不改变剩余字符顺序的情况下，删除某些字符或者不删除任何字符形成的一个序列。

  • 思路：注意回文子序列一定要动态规划，因为暴力解法是2^n次
  • 关键是如何设置DP数组
  • 
  • 难点：遍历顺序和初始化的值。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

  class Solution { public: int longestPalindromeSubseq(string s) { int n=s.size(); vector<vector<int>> dp(n,vector<int>(n,0)); for(int i=0;i<n;++i){ dp[i][i]=1; } for(int i=n-1;i>=0;--i){ for(int j=i+1;j<n;++j){ if(s[i]==s[j]){ dp[i][j]=dp[i+1][j-1]+2; }else{ dp[i][j]=max(dp[i+1][j],dp[i][j-1]); } } } return dp[0][n-1]; } };

• 562. 矩阵中最长的连续1线段

  给定一个01矩阵 M，找到矩阵中最长的连续1线段。这条线段可以是水平的、垂直的、对角线的或者反对角线的。

  • 思路：分四个二维dp数组，分别表示横、竖、斜、反斜

  • dp的定义是到[i][j]的时候横或其他三种的连续1的最大值

  • 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99

    class Solution { public: int longestLine(vector<vector<int>>& mat) { int n=mat.size(); int m=mat[0].size(); vector<vector<int>> dp(n,vector<int>(m,0));//竖着 vector<vector<int>> dp_r(n,vector<int>(m,0));//反斜线 vector<vector<int>> dp_row(n,vector<int>(m,0));//横着 vector<vector<int>> dp_vr(n,vector<int>(m,0));//正斜线 int len=0; //dp dp[0][0]=mat[0][0]==1 ? 1: 0; for(int i=1;i<m;++i){ if(mat[0][i]==1){ dp[0][i]=1; }else{ dp[0][i]=0; } len=max(len,dp[0][i]); } for(int i=1;i<n;++i){ for(int j=0;j<m;++j){ if(mat[i][j]==1){ dp[i][j]=dp[i-1][j]+1; len=max(len,dp[i][j]); } } } //dp_r dp_r[0][m-1]=mat[0][m-1]==1 ? 1: 0; for(int i=m-2;i>=0;--i){ if(mat[0][i]==1){ dp_r[0][i]=1; }else{ dp_r[0][i]=0; } len=max(len,dp_r[0][i]); } for(int i=1;i<n;++i){ if(mat[i][m-1]==1){ dp_r[i][m-1]=1; }else{ dp_r[i][m-1]=0; } len=max(len,dp_r[i][m-1]); } for(int i=1;i<n;++i){ for(int j=0;j<m-1;++j){ if(mat[i][j]==1){ dp_r[i][j]=dp_r[i-1][j+1]+1; len=max(len,dp_r[i][j]); } } } //dp_row for(int i=0;i<n;++i){ if(mat[i][0]==1){ dp_row[i][0]=1; len=max(len,dp_row[i][0]); } } for(int i=0;i<n;++i){ for(int j=1;j<m;++j){ if(mat[i][j]==1){ dp_row[i][j]=dp_row[i][j-1]+1; len=max(len,dp_row[i][j]); } } } //dp_rv for(int i=0;i<m;++i){ if(mat[0][i]==1){ dp_vr[0][i]=1; len=max(dp_vr[0][i],len); } } for(int i=1;i<n;++i){ if(mat[i][0]==1){ dp_vr[i][0]=1; len=max(len,dp_vr[i][0]); } } for(int i=1;i<n;++i){ for(int j=1;j<m;++j){ if(mat[i][j]==1){ dp_vr[i][j]=dp_vr[i-1][j-1]+1; len=max(len,dp_vr[i][j]); } } } return len; } };

• 1182. 与目标颜色间的最短距离

  给你一个数组 colors，里面有 1、2、 3 三种颜色。

  我们需要在 colors 上进行一些查询操作 queries，其中每个待查项都由两个整数 i 和 c 组成。

  现在请你帮忙设计一个算法，查找从索引 i 到具有目标颜色 c 的元素之间的最短距离。

  如果不存在解决方案，请返回 -1。

  • 示例

  输入：colors = [1,1,2,1,3,2,2,3,3], queries = [[1,3],[2,2],[6,1]] 输出：[3,0,3] 解释： 距离索引 1 最近的颜色 3 位于索引 4（距离为 3）。 距离索引 2 最近的颜色 2 就是它自己（距离为 0）。 距离索引 6 最近的颜色 1 位于索引 3（距离为 3）。

  • 思路1：设立三个颜色位置数组，然后使用二分查找，找到最近的值
    • 要么直接相等
    • 要么一个小于一个大于，在中间，返回绝对值的min值

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80

  class Solution { public: //直接返回最短距离 int sort_bind(vector<int> &nums, int left ,int right,int tar){ if(nums[left]>=tar){ return nums[left]-tar; } if(nums[right]<=tar){ return tar-nums[right]; } while(left<right){ int temp=(left+right)/2; if(nums[temp]==tar){ return nums[temp]-tar; }else if(nums[temp]>tar){ if(temp-1>=0 && nums[temp-1]<=tar){ return min(abs(nums[temp]-tar),abs(nums[temp-1]-tar)); }else{ right=temp-1; } }else if(nums[temp]<tar){ if(temp+1<nums.size() && nums[temp+1]>=tar){ return min(abs(nums[temp]-tar),abs(nums[temp+1]-tar)); }else{ left=temp+1; } } } return abs(nums[left]-tar); } vector<int> shortestDistanceColor(vector<int>& colors, vector<vector<int>>& queries) { vector<int> color1; vector<int> color2; vector<int> color3; int n=colors.size(); for(int i=0;i<n;++i){ if(colors[i]==1){ color1.push_back(i); }else if(colors[i]==2){ color2.push_back(i); }else if(colors[i]==3){ color3.push_back(i); } } int m=queries.size(); vector<int> out; for(int i=0;i<m;++i){ vector<int> temp=queries[i]; int ret; //二分查找返回索引绝对值差值 if(temp[1]==1){ if(color1.size()==0){ ret=-1; }else{ ret=sort_bind(color1, 0, color1.size()-1, temp[0]); } }else if(temp[1]==2){ if(color2.size()==0){ ret=-1; }else { ret=sort_bind(color2, 0, color2.size()-1, temp[0]); } }else if(temp[1]==3){ if(color3.size()==0){ ret=-1; }else{ ret=sort_bind(color3, 0, color3.size()-1, temp[0]); } }else { ret=-1; } out.push_back(ret); } return out; } };

  • 思路2：使用动态规划
  • 使用两个三维数组，分别表示左右的颜色1.2.3的距离，最后比较即可

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123

  class Solution { public: vector<int> shortestDistanceColor(vector<int>& colors, vector<vector<int>>& queries) { int n=colors.size(); vector<vector<int>> dpleft(3,vector<int>(n,0));//从左往右 vector<vector<int>> dpright(3,vector<int>(n,0)); dpleft[0][0]=colors[0]==1? 0:INT_MAX; dpleft[1][0]=colors[0]==2? 0:INT_MAX; dpleft[2][0]=colors[0]==3? 0:INT_MAX; dpright[0][n-1]=colors[n-1]==1? 0:INT_MAX; dpright[1][n-1]=colors[n-1]==2? 0:INT_MAX; dpright[2][n-1]=colors[n-1]==3? 0:INT_MAX; for(int i=1;i<n;++i){ switch (colors[i]){ case 1: dpleft[0][i]=0; if(dpleft[1][i-1]!=INT_MAX){ dpleft[1][i]=dpleft[1][i-1]+1; }else{ dpleft[1][i]=INT_MAX; } if(dpleft[2][i-1]!=INT_MAX){ dpleft[2][i]=dpleft[2][i-1]+1; }else{ dpleft[2][i]=INT_MAX; } break; case 2: dpleft[1][i]=0; if(dpleft[0][i-1]!=INT_MAX){ dpleft[0][i]=dpleft[0][i-1]+1; }else{ dpleft[0][i]=INT_MAX; } if(dpleft[2][i-1]!=INT_MAX){ dpleft[2][i]=dpleft[2][i-1]+1; }else{ dpleft[2][i]=INT_MAX; } break; case 3: dpleft[2][i]=0; if(dpleft[1][i-1]!=INT_MAX){ dpleft[1][i]=dpleft[1][i-1]+1; } else{ dpleft[1][i]=INT_MAX; } if(dpleft[0][i-1]!=INT_MAX){ dpleft[0][i]=dpleft[0][i-1]+1; }else{ dpleft[0][i]=INT_MAX; } break; } } for(int i=n-2;i>=0;--i){ switch (colors[i]){ case 1: dpright[0][i]=0; if(dpright[1][i+1]!=INT_MAX){ dpright[1][i]=dpright[1][i+1]+1; }else{ dpright[1][i]=INT_MAX; } if(dpright[2][i+1]!=INT_MAX){ dpright[2][i]=dpright[2][i+1]+1; }else{ dpright[2][i]=INT_MAX; } break; case 2: dpright[1][i]=0; if(dpright[0][i+1]!=INT_MAX){ dpright[0][i]=dpright[0][i+1]+1; }else{ dpright[0][i]=INT_MAX; } if(dpright[2][i+1]!=INT_MAX){ dpright[2][i]=dpright[2][i+1]+1; }else{ dpright[2][i]=INT_MAX; } break; case 3: dpright[2][i]=0; if(dpright[1][i+1]!=INT_MAX){ dpright[1][i]=dpright[1][i+1]+1; } else{ dpright[1][i]=INT_MAX; } if(dpright[0][i+1]!=INT_MAX){ dpright[0][i]=dpright[0][i+1]+1; }else{ dpright[0][i]=INT_MAX; } break; } } vector<int> ret; for(int j=0;j<queries.size();++j){ vector<int> temp=queries[j]; int a=dpleft[temp[1]-1][temp[0]]; int b=dpright[temp[1]-1][temp[0]]; int out; if(a==INT_MAX &&b ==INT_MAX){ out=-1; ret.push_back(out); }else{ out=min(a,b); ret.push_back(out); } } return ret; } };

• 343. 整数拆分

  给定一个正整数 n，将其拆分为至少两个正整数的和，并使这些整数的乘积最大化。 返回你可以获得的最大乘积。

  • 思路：动态规划

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

  //递推方程 //dp[i]=max(dp[i-j]*j,(i-j)*j,dp[i]);到i的时候的乘积最大值，类似分蛋糕 class Solution { public: int integerBreak(int n) { if(n==1 || n==2){ return 1; } vector<int> dp(n+1,0); dp[0]=dp[1]=dp[2]=1; for(int i=3;i<=n;++i){ for(int j=1;j<i;++j){ int temp1=dp[i-j]*j; int temp2=(i-j)*j; dp[i]=max(dp[i],max(temp1,temp2)); } } return dp[n]; } };

• 238. 除自身以外数组的乘积

  给你一个长度为 n 的整数数组 nums，其中 n > 1，返回输出数组 output ，其中 output[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积。

  提示：题目数据保证数组之中任意元素的全部前缀元素和后缀（甚至是整个数组）的乘积都在 32 位整数范围内。

  说明: 请不要使用除法，且在 O(n) 时间复杂度内完成此题。

  • 思路：使用前后缀和，类似于有多少个pat的那个题目

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

  class Solution { public: vector<int> productExceptSelf(vector<int>& nums) { //使用前后缀合处理 int n=nums.size(); vector<int> dp1(n,0); vector<int> dp2(n,0); dp1[0]=1; dp2[n-1]=1; for(int i=1;i<n;++i){ dp1[i]=dp1[i-1]*nums[i-1]; } for(int i=n-2;i>=0;--i){ dp2[i]=dp2[i+1]*nums[i+1]; } vector<int> ret(n,0); for(int i=0;i<n;++i){ ret[i]=dp1[i]*dp2[i]; } return ret; } };

• 139. 单词拆分

  给你一个字符串 s 和一个字符串列表 wordDict 作为字典，判定 s 是否可以由空格拆分为一个或多个在字典中出现的单词。

  说明: 拆分时可以重复使用字典中的单词。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38

  //dp定义——到string[i]的时候可不可以被拆分。一个bool类型 class Solution { public: //闭区间 //优化的地方可以使用哈希表进行查找，直接string相等比较费时 bool check(string s, int left, int right,vector<string>& wordDict){ int n=wordDict.size(); string temp=s.substr(left,right-left+1); for(int i=0;i<n;++i){ if(wordDict[i]==temp){ return true;; } } return false; } bool wordBreak(string s, vector<string>& wordDict) { int n=s.size(); vector<bool> dp(n,false); if(check(s, 0, 0,wordDict)){ dp[0]=true; } for(int i=1;i<n;++i){ if(check(s, 0, i, wordDict)){ dp[i]=true;//剪枝 continue; } for(int j=0;j<i;++j){ if(dp[j]==true &&check(s, j+1, i, wordDict)){ dp[i]=true; break; } } } return dp[n-1]; } };

• 62. 不同路径

  一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

  机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

  问总共有多少条不同的路径？

  1 2 3 4 5 6 7 8 9 10 11 12 13 14

  //思路：设置dp数组，定义为到[i][j]点的时候的路径总数目。初始化第一行和第一列均为1，递推公式为dp[i][j]=dp[i-1][j]+dp[i][j-1]; class Solution { public: int uniquePaths(int m, int n) { vector<vector<int>> dp(m,vector<int>(n,1)); for(int i=1;i<m;++i){ for(int j=1;j<n;++j){ dp[i][j]=dp[i-1][j]+dp[i][j-1]; } } return dp[m-1][n-1]; } };

• 63. 不同路径 II

  一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

  机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

  现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

  网格中的障碍物和空位置分别用 1 和 0 来表示。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37

  //思路，如果等于1，dp[i][j]=0;不等于1,dp[i][j]=dp[i-1][j]+dp[i][j-1]; //初始化第一行第一列记得根据之前的判断 class Solution { public: int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) { int n=obstacleGrid.size(); int m=obstacleGrid[0].size(); vector<vector<int>> dp(n,vector<int>(m,0)); //初始化第一行 dp[0][0]=obstacleGrid[0][0]==1 ? 0:1; for(int i=1;i<m;++i){ if(obstacleGrid[0][i]==1){ dp[0][i]=0; }else{ dp[0][i]=dp[0][i-1]; } } //初始化第一列 for(int i=1;i<n;++i){ if(obstacleGrid[i][0]==1){ dp[i][0]=0; }else{ dp[i][0]=dp[i-1][0]; } } for(int i=1;i<n;++i){ for(int j=1;j<m;++j){ if(obstacleGrid[i][j]==1){ dp[i][j]=0; }else{ dp[i][j]=dp[i-1][j]+dp[i][j-1]; } } } return dp[n-1][m-1]; } };

• 650. 只有两个键的键盘

  最初记事本上只有一个字符 'A' 。你每次可以对这个记事本进行两种操作：

  • Copy All（复制全部）：复制这个记事本中的所有字符（不允许仅复制部分字符）。
  • Paste（粘贴）：粘贴 上一次 复制的字符。

  给你一个数字 n ，你需要使用最少的操作次数，在记事本上输出 恰好 n 个 'A' 。返回能够打印出 n 个 'A' 的最少操作次数。

  

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

  class Solution { public: int minSteps(int n) { if(n==1){ return 0; } if(n==2){ return 2; } vector<int> dp(n+1,INT_MAX); dp[1]=0; dp[2]=2; for(int i=3;i<=n;++i){ dp[i]=min(dp[i],i); for(int j=2;j<=i;++j){ if(i%j==0){ dp[i]=min(dp[i],dp[j]+i/j); } } } return dp[n]; } }; //可以优化的点是，只是遍历到根号处,但要记得因子互换，不然没有完全遍历 for(int j=2;j*j<=i;++j){ if(i%j==0){ dp[i]=min(dp[i],dp[j]+i/j); dp[i]=min(dp[i/j],dp[i/j]+j); } }

  • 思路二：分解质因数

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

  /*例如：18=2*9 3*6 6*3 6=2*3 当最后是质数n，操作数目也是n（copy1次，pasten-1次) 2*3表示复制1次2，粘贴2次2，最后还是3次 所以6最终是2+3=5次 然后6*3再来3次，就是8次 // 总结，分解成比n小的依次非递减的序列相乘的和，就是返回的次数 18=2*3*3 return 2+3+3 */ class Solution { public: int minSteps(int n) { if(n==1){ return 0; } int ans=0; for(int i=2;i*i<=n;++i){ while(n%i==0){ n=n/i; ans+=i; } } if(n!=1){ ans+=n; } return ans; } };

• 361. 轰炸敌人

  想象一下炸弹人游戏，在你面前有一个二维的网格来表示地图，网格中的格子分别被以下三种符号占据：

  • 'W' 表示一堵墙
  • 'E' 表示一个敌人
  • '0'（数字 0）表示一个空位

  请你计算一个炸弹最多能炸多少敌人。

  由于炸弹的威力不足以穿透墙体，炸弹只能炸到同一行和同一列没被墙体挡住的敌人。

  注意: 你只能把炸弹放在一个空的格子里

  • 思路：朴素的想法是直接暴力破解，耗时，还有很多重复的，O(n3)。
  • 改进思路：使用4个dp数组，分别表示上下左右的敌人个数，遍历数组三次输出

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59

  class Solution { public: int maxKilledEnemies(vector<vector<char>>& grid) { int ret=0; int n=grid.size(); int m=grid[0].size(); vector<vector<int>> dp(n,vector<int>(m,0));//左 vector<vector<int>> dp1(n,vector<int>(m,0));//上 vector<vector<int>> dp2(n,vector<int>(m,0));//右 vector<vector<int>> dp3(n,vector<int>(m,0));//下 for(int i=0;i<grid.size();++i){ for(int j=0;j<grid[0].size();++j){ if(grid[i][j]=='W'){ dp[i][j]=0; dp1[i][j]=0; }else{ if(grid[i][j]=='E'){ dp[i][j]=1;//包括自己 dp1[i][j]=1; } if(j-1>=0){ dp[i][j]+=dp[i][j-1]; } if(i-1>=0){ dp1[i][j]+=dp1[i-1][j]; } } } } for(int i=n-1;i>=0;--i){ for(int j=m-1;j>=0;--j){ if(grid[i][j]=='W'){ dp2[i][j]=0; dp3[i][j]=0; }else{ if(grid[i][j]=='E'){ dp2[i][j]=1;//包括自己 dp3[i][j]=1; } if(j+1<m){ dp2[i][j]+=dp2[i][j+1]; } if(i+1<n){ dp3[i][j]+=dp3[i+1][j]; } } } } for(int i=0;i<n;++i){ for(int j=0;j<m;++j){ if(grid[i][j]=='0'){ ret=max(ret,dp[i][j]+dp1[i][j]+dp2[i][j]+dp3[i][j]); } } } return ret; } };

• 279. 完全平方数

  给定正整数 n，找到若干个完全平方数（比如 1, 4, 9, 16, ...）使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。

  给你一个整数 n ，返回和为 n 的完全平方数的 最少数量 。

  完全平方数 是一个整数，其值等于另一个整数的平方；换句话说，其值等于一个整数自乘的积。例如，1、4、9 和 16 都是完全平方数，而 3 和 11 不是。

  • 思路：dp[i]=1+min(dp[i-j*j])；j从1到根号n

  • 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

    class Solution { public: int numSquares(int n) { vector<int> dp(n+1,INT_MAX); if(n==1){ return 1; } dp[0]=0; dp[1]=1; for(int i=2;i<=n;++i){ for(int j=1;j*j<=i;++j){ dp[i]=min(dp[i],dp[i-j*j]+1); } } return dp[n]; } };

跳跃游戏

• 55. 跳跃游戏

  给定一个非负整数数组 nums ，你最初位于数组的 第一个下标 。

  数组中的每个元素代表你在该位置可以跳跃的最大长度。

  判断你是否能够到达最后一个下标。

  提供两种思路：

  思路1：定义dp数组为能否跳到i位置，双重for循环，注意第二次逆向循环，更快 思路2：转换为求最值问题，定义max_len，当前位置到达的最远距离，最后返回是否大于等于n-1

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35

  class Solution { public: bool canJump(vector<int>& nums) { // //题解1： // int n=nums.size(); // //我设置的dp数组定义：能否跳到i位置 // vector<bool> dp(n,false); // dp[0]=true; // for(int i=1;i<n;++i){ // //注意逆向排序，这样更快 // for(int j=i-1;j>=0;--j){ // int reduce=i-j; // if(dp[j]&&nums[j]>=reduce){ // dp[i]=true; // break;//退出内层循环 // } // } // } // return dp[n-1]; //题解2：转化为简单的定义，最长的跳跃长度 int n=nums.size(); int max_len=nums[0]; for(int i=1;i<n;++i){ if(i>max_len){ //证明无法到达这个位置，更别说最后了 return false; }else{ //求出max_len max_len=max(max_len,i+nums[i]); } } return max_len>=(n-1); } };

• 45. 跳跃游戏 II

  给你一个非负整数数组 nums ，你最初位于数组的第一个位置。

  数组中的每个元素代表你在该位置可以跳跃的最大长度。

  你的目标是使用最少的跳跃次数到达数组的最后一个位置。

  假设你总是可以到达数组的最后一个位置。

  提供两种思路：

  思路1：直接dp穷举，dp定义为到达位置i的最短步数，双重for循环。 思路2：贪心算法，类似BFS，在每一层遍历找最远的距离作为下一次的末尾，每遍历一层，次数+1，注意只需要遍历前n-1个位置，因为始终会到达的。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34

  class Solution { public: int jump(vector<int>& nums) { // //解法一：穷举，n^2时间复杂度 // int n=nums.size(); // vector<int> dp(n,INT_MAX); // dp[0]=0; // for(int i=1;i<n;++i){ // for(int j=0;j<i;++j){ // if(j+nums[j]>=i){ // dp[i]=min(dp[i],dp[j]+1); // } // } // } // return dp[n-1]; //解法2：贪心算法，我的理解是类似BFS int n=nums.size(); int end=0;//bfs栈的大小 int max_len=0;//最长的距离,和end互相迭代 int step=0;//最短步数 //进行前n-1个即可,最后一个不用，因为始终会到达 for(int i=0;i<n-1;++i){ //先更新长度，因为从零开始 max_len=max(max_len,i+nums[i]); if(i==end){ end=max_len; ++step; } } return step; } };

青蛙跳台变种

• 91. 解码方法

  一条包含字母 A-Z 的消息通过以下映射进行了 编码 ：

  'A' -> 1
  'B' -> 2
  ...
  'Z' -> 26
  

  要 解码 已编码的消息，所有数字必须基于上述映射的方法，反向映射回字母（可能有多种方法）。例如，"11106" 可以映射为：

  • "AAJF" ，将消息分组为 (1 1 10 6)
  • "KJF" ，将消息分组为 (11 10 6)

  注意，消息不能分组为 (1 11 06) ，因为 "06" 不能映射为 "F" ，这是由于 "6" 和 "06" 在映射中并不等价。

  给你一个只含数字的 非空 字符串 s ，请计算并返回 解码 方法的 总数 。

  题目数据保证答案肯定是一个 32 位 的整数。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23

  class Solution { public: //类似青蛙跳台，可以跳一级，也可以调两级，关键是如何判别 //取巧，所有初始化为0.只探讨两种情况，不在情况的延续0，最后输出即可 int numDecodings(string s) { int n=s.size(); vector<int> dp(n+1,0); //初始化，无符号有一种解法 dp[0]=1; for(int i=1;i<=n;++i){ //条件1：取一个符号 if(s[i-1]!='0'){ dp[i]+=dp[i-1]; } //条件2：取两个符号 if(i>=2&&s[i-2]!='0'&&(10*(s[i-2]-'0')+(s[i-1]-'0')<=26)){ dp[i]+=dp[i-2]; } //其他情况延续0，最后输出也是0；所以就不用纠结分类讨论 } return dp[n]; } };

• 221. 最大正方形

  在一个由 '0' 和 '1' 组成的二维矩阵内，找到只包含 '1' 的最大正方形，并返回其面积。

  • 暴力解法：遍历元素1，认为当前是左上角顶点，依次找最大可能的正方形面积，然后验证。

  • 思路：定义dp[i][j] 表示以i行j 列为正方形右下角顶点的最大正方形边长

  • 递推公式$dp[i][j]=min(dp[i-1][j],dp[i-1][j-1],dp[i][j-1])+1$

  • 最后返回dp的最大值就可以了。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37

  class Solution { public: int maximalSquare(vector<vector<char>>& matrix) { int rows=matrix.size(); int cols=matrix[0].size(); vector<vector<int>> dp(rows,vector<int>(cols,0)); int ret=0; //初始化第一行 for(int i=0;i<cols;++i){ if(matrix[0][i]=='1'){ dp[0][i]=1; ret=max(ret,1); } } //初始化第一列 for(int i=1;i<rows;++i){ if(matrix[i][0]=='1'){ dp[i][0]=1; ret=max(ret,1); } } //动规 for(int i=1;i<rows;++i){ for(int j=1;j<cols;++j){ if(matrix[i][j]=='1'){ if(dp[i-1][j-1]&&dp[i-1][j]&&dp[i][j-1]){ dp[i][j]=min(min(dp[i-1][j-1],dp[i-1][j]),dp[i][j-1])+1; }else{ dp[i][j]=1; } ret=max(ret,dp[i][j]); } } } return ret*ret; } };

预测赢家和堆石子

• 486. 预测赢家

  给你一个整数数组 nums 。玩家 1 和玩家 2 基于这个数组设计了一个游戏。

  玩家 1 和玩家 2 轮流进行自己的回合，玩家 1 先手。开始时，两个玩家的初始分值都是 0 。每一回合，玩家从数组的任意一端取一个数字（即，nums[0] 或 nums[nums.length - 1]），取到的数字将会从数组中移除（数组长度减 1 ）。玩家选中的数字将会加到他的得分上。当数组中没有剩余数字可取时，游戏结束。

  如果玩家 1 能成为赢家，返回 true 。如果两个玩家得分相等，同样认为玩家 1 是游戏的赢家，也返回 true 。你可以假设每个玩家的玩法都会使他的分数最大化。

  • 思路1：暴力解法，递归，由底向上，类似二叉树的后序遍历，不同的是需要分开哪一个是先手和后手。

  • 

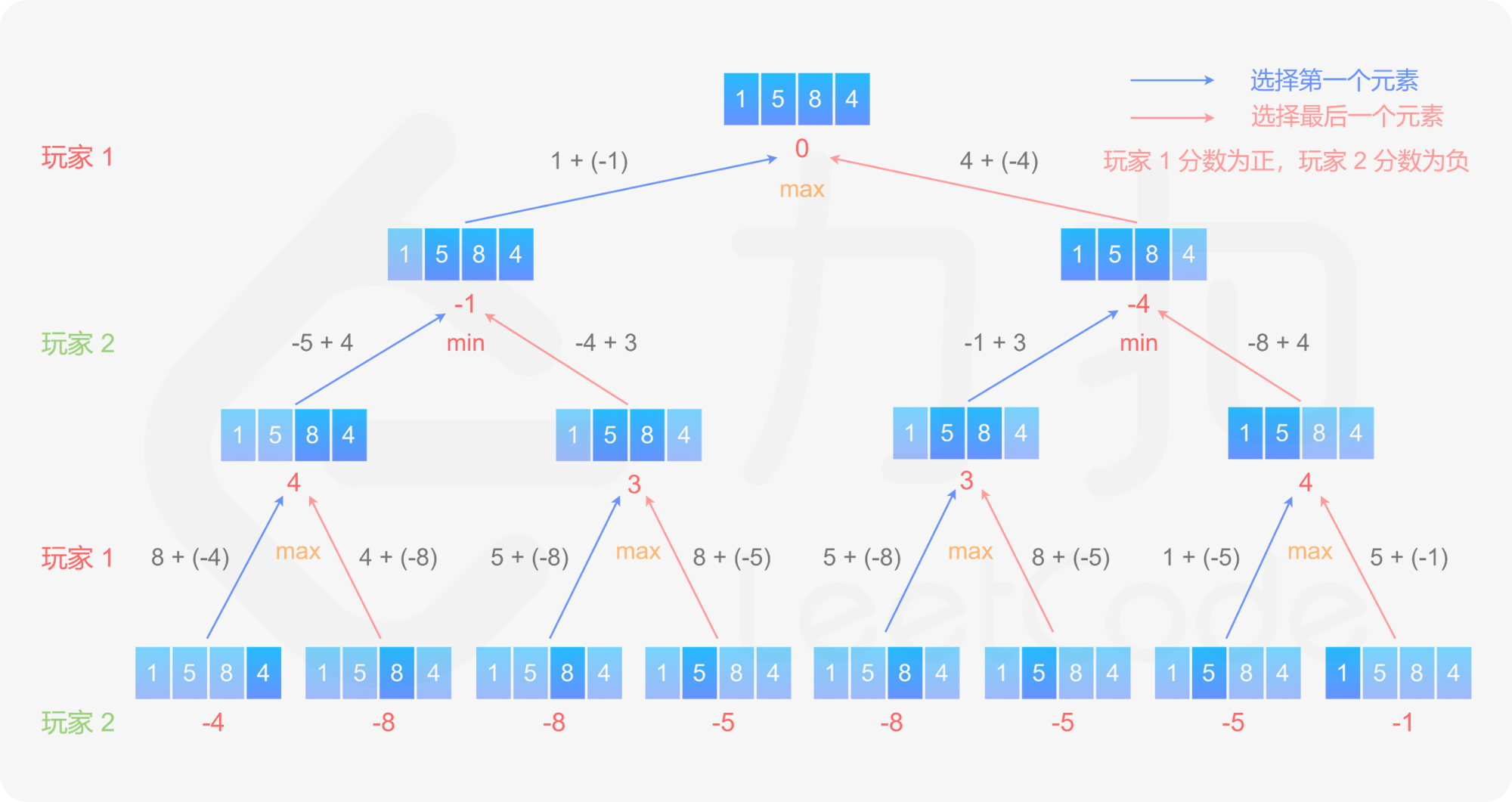
  • 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

    class Solution { public: int getMax(vector<int>& nums,int left, int right,int turn){ //递归结束条件 if(left==right){ return nums[left]*turn; } //取首位 int leftScore=nums[left]*turn+getMax(nums, left+1, right,-turn); //取末尾 int rightScor=nums[right]*turn+getMax(nums, left, right-1,-turn); if(turn==1){ return max(leftScore,rightScor); }else{ return min(leftScore,rightScor); } } bool PredictTheWinner(vector<int>& nums) { int left=0; int right=nums.size()-1; int turn=1; return getMax(nums,left,right,turn)>=0; } };

  • 

  • 因此，可以省略上述的turn变量判断先手与否，只要最后的数值是否大于等于0即可

  • 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

    class Solution { public: int getMax(vector<int>& nums,int left, int right){ //递归结束条件 if(left==right){ return nums[left]; } //取首位 int leftScore=nums[left]-getMax(nums, left+1, right); //取末尾 int rightScor=nums[right]-getMax(nums, left, right-1); return max(leftScore,rightScor); } bool PredictTheWinner(vector<int>& nums) { int right=nums.size()-1; return getMax(nums,0,right)>=0; } };

  • 思路2：动态规划，上面的暴力求解有很大部分重复求解，因此可以使用动态规划，定义二维数组dp[i][j] 表示nums的第i 个元素到第j 个元素玩家赢面，很明显根据第二种暴力的优化，可以得出递推公式。dp[i][j]=max(nums[i]-dp[i+1][j],nums[j]-dp[i][j-1]) 。

  • 

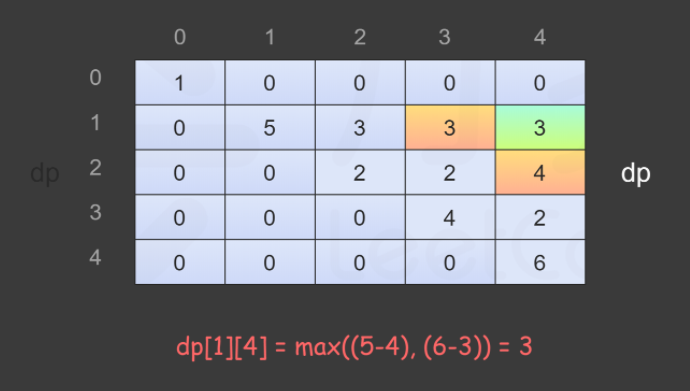
  • 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

    class Solution { public: bool PredictTheWinner(vector<int>& nums) { int rows=nums.size(); vector<vector<int>> dp(rows,vector<int>(rows,0)); //初始化 for(int i=0;i<rows;++i){ dp[i][i]=nums[i]; } for(int i=rows-2;i>=0;--i){ for(int j=i+1;j<rows;++j){ int temp=max(nums[i]-dp[i+1][j],nums[j]-dp[i][j-1]); dp[i][j]=temp; } } return dp[0][rows-1]>=0; } };

  • 其实，只要数组的个数是偶数，先手必然有赢的机会。可以这么想，如果开始先手不慎输了，那么重来，走赢的人的路必然可以赢。而数组的个数是奇数，才需要动态规划。

• 877. 石子游戏

  Alice 和 Bob 用几堆石子在做游戏。一共有偶数堆石子，排成一行；每堆都有 正 整数颗石子，数目为 piles[i] 。

  游戏以谁手中的石子最多来决出胜负。石子的 总数 是 奇数 ，所以没有平局。

  Alice 和 Bob 轮流进行，Alice 先开始 。 每回合，玩家从行的 开始 或 结束 处取走整堆石头。 这种情况一直持续到没有更多的石子堆为止，此时手中 石子最多 的玩家 获胜 。

  假设 Alice 和 Bob 都发挥出最佳水平，当 Alice 赢得比赛时返回 true ，当 Bob 赢得比赛时返回 false 。

  • 思路1：动态规划

  • 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

    class Solution { public: bool stoneGame(vector<int>& piles) { int n=piles.size(); vector<vector<int>> dp(n,vector<int>(n,0)); for(int i=0;i<n;++i){ dp[i][i]=piles[i]; } for(int i=n-2;i>=0;--i){ for(int j=i+1;j<n;++j){ dp[i][j]=max(piles[j]-dp[i][j-1],piles[i]-dp[i+1][j]); } } return dp[0][n-1]>0; } };

  • 思路2：数学推理，偶数，总数不能平分，先手必然有赢的可能

  • 1 2 3 4 5 6

    class Solution { public: bool stoneGame(vector<int>& piles) { return true; } };

• 983. 最低票价

  在一个火车旅行很受欢迎的国度，你提前一年计划了一些火车旅行。在接下来的一年里，你要旅行的日子将以一个名为 days 的数组给出。每一项是一个从 1 到 365 的整数。

  火车票有 三种不同的销售方式 ：

  • 一张 为期一天 的通行证售价为 costs[0] 美元；
  • 一张 为期七天 的通行证售价为 costs[1] 美元；
  • 一张 为期三十天 的通行证售价为 costs[2] 美元。

  通行证允许数天无限制的旅行。 例如，如果我们在第 2 天获得一张 为期 7 天 的通行证，那么我们可以连着旅行 7 天：第 2 天、第 3 天、第 4 天、第 5 天、第 6 天、第 7 天和第 8 天。

  返回 你想要完成在给定的列表 days 中列出的每一天的旅行所需要的最低消费 。

  • 思路：一步一步动规往前。memo[i] 表示到第i天旅游的最小花费。
  • 以下是优化代码：判断这一天要不要旅游可以使用哈希表。
  • 

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

  class Solution { public: int mincostTickets(vector<int>& days, vector<int>& costs) { int last=days.back(); int memo[last+1]; memset(memo, 0, sizeof(memo)); int dateIdx=0;//days的序号 for(int i=1;i<=last;++i){ if(days[dateIdx]!=i){ //判读这一天需不需要旅游 memo[i]=memo[i-1];//等于前一天的花费 }else{ //考虑三种情况，注意边缘情况 int temp1=memo[(i-1)>=0?i-1:0]+costs[0]; int temp2=memo[(i-7)>=0?i-7:0]+costs[1]; int temp3=memo[(i-30)>=0?i-30:0]+costs[2]; memo[i]=min(temp1,min(temp2,temp3)); //注意序号加1 ++dateIdx; } } return memo[last]; } };

贪心算法

• 动态规划具有三个性质：

  1）重叠子问题

  2）最优子结构

  3. 状态转移方程

  贪心算法：

  1）贪心选择性质

  2）最优子结构

  反过来说就是，我们可以通过子问题的最优解，推导出问题的最优解。

  解释一下，最优子结构性质是指问题的最优解包含其子问题的最优解时，就称该问题具有最优子结构性质，重叠子问题指的是子问题可能被多次用到，多次计算，动态规划就是为了消除其重叠子问题而设计的。其实贪心算法是一种特殊的动态规划，由于其具有贪心选择性质，保证了子问题只会被计算一次，不会被多次计算，因此贪心算法其实是最简单的动态规划。

• 「解决一个问题需要多个步骤，每一个步骤有多种选择」这样的描述我们在「回溯算法」「动态规划」算法中都会看到。它们的区别如下：

  「回溯算法」需要记录每一个步骤、每一个选择，用于回答所有具体解的问题； 「动态规划」需要记录的是每一个步骤、所有选择的汇总值（最大、最小或者计数）； 「贪心算法」由于适用的问题，每一个步骤只有一种选择，一般而言只需要记录与当前步骤相关的变量的值。

• 435. 无重叠区间

  给定一个区间的集合，找到需要移除区间的最小数量，使剩余区间互不重叠。

  注意:

  1. 可以认为区间的终点总是大于它的起点。
  2. 区间 [1,2] 和 [2,3] 的边界相互“接触”，但没有相互重叠。

• 605. 种花问题

  假设有一个很长的花坛，一部分地块种植了花，另一部分却没有。可是，花不能种植在相邻的地块上，它们会争夺水源，两者都会死去。

  给你一个整数数组 flowerbed 表示花坛，由若干 0 和 1 组成，其中 0 表示没种植花，1 表示种植了花。另有一个数 n ，能否在不打破种植规则的情况下种入 n 朵花？能则返回 true ，不能则返回 false。

• 452. 用最少数量的箭引爆气球

  在二维空间中有许多球形的气球。对于每个气球，提供的输入是水平方向上，气球直径的开始和结束坐标。由于它是水平的，所以纵坐标并不重要，因此只要知道开始和结束的横坐标就足够了。开始坐标总是小于结束坐标。

  一支弓箭可以沿着 x 轴从不同点完全垂直地射出。在坐标 x 处射出一支箭，若有一个气球的直径的开始和结束坐标为 x``start，x``end， 且满足 xstart ≤ x ≤ xend，则该气球会被引爆。可以射出的弓箭的数量没有限制。 弓箭一旦被射出之后，可以无限地前进。我们想找到使得所有气球全部被引爆，所需的弓箭的最小数量。

  给你一个数组 points ，其中 points [i] = [xstart,xend] ，返回引爆所有气球所必须射出的最小弓箭数。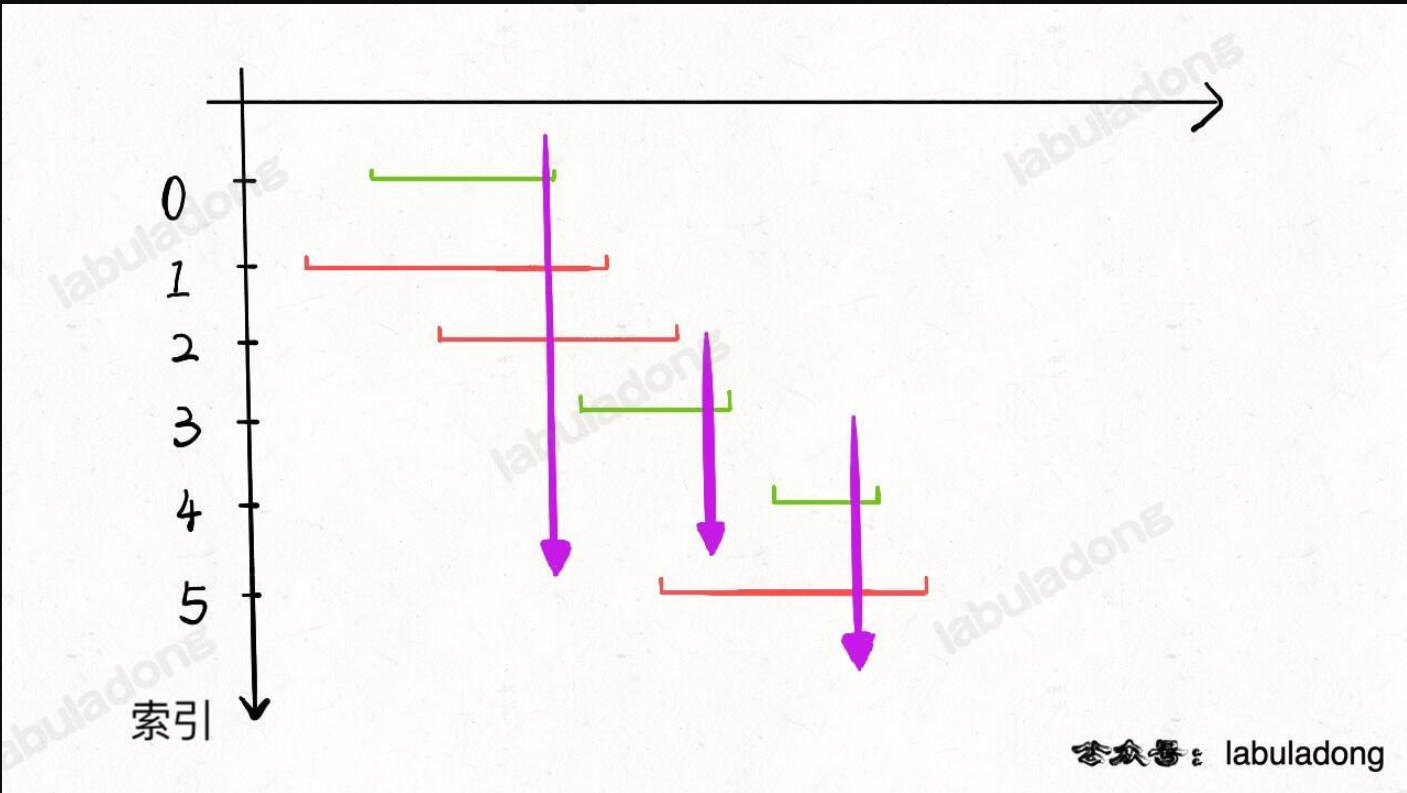

  

• 757. 设置交集大小至少为2

  难度困难159

  一个整数区间 [a, b] ( a < b ) 代表着从 a 到 b 的所有连续整数，包括 a 和 b。

  给你一组整数区间intervals，请找到一个最小的集合 S，使得 S 里的元素与区间intervals中的每一个整数区间都至少有2个元素相交。

  输出这个最小集合S的大小。

  示例 1:

  1 2 3 4 5

  输入: intervals = [[1, 3], [1, 4], [2, 5], [3, 5]] 输出: 3 解释: 考虑集合 S = {2, 3, 4}. S与intervals中的四个区间都有至少2个相交的元素。 且这是S最小的情况，故我们输出3。

• 思路：452射箭问题的升级版，都是排序+贪心的思路。

• 

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

  class Solution { public: int intersectionSizeTwo(vector<vector<int>>& intervals) { int n = intervals.size(); if(n==1){ return 2; } sort(intervals.begin(),intervals.end(),[](auto &a1, auto &a2){ return a1[0]<a2[0]; }); int start = intervals.back()[0]; int end = start+1; int k = n-2; while(k>=0){ if(intervals[k][1]>start){ --k; continue; }else{ start = intervals[k][1]-1; --k; } } return end-start+1; } };

• 763. 划分字母区间

  字符串 S 由小写字母组成。我们要把这个字符串划分为尽可能多的片段，同一字母最多出现在一个片段中。返回一个表示每个字符串片段的长度的列表。

• 122. 买卖股票的最佳时机 II

  给定一个数组 prices ，其中 prices[i] 是一支给定股票第 i 天的价格。

  设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易（多次买卖一支股票）。

  **注意：**你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

• 406. 根据身高重建队列

  假设有打乱顺序的一群人站成一个队列，数组 people 表示队列中一些人的属性（不一定按顺序）。每个 people[i] = [hi, ki] 表示第 i 个人的身高为 hi ，前面 正好 有 ki 个身高大于或等于 hi 的人。

  请你重新构造并返回输入数组 people 所表示的队列。返回的队列应该格式化为数组 queue ，其中 queue[j] = [hj, kj] 是队列中第 j 个人的属性（queue[0] 是排在队列前面的人）。

  • people = [[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]] 输出：[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]]

  

• 665. 非递减数列

  给你一个长度为 n 的整数数组，请你判断在 最多 改变 1 个元素的情况下，该数组能否变成一个非递减数列。

  我们是这样定义一个非递减数列的： 对于数组中任意的 i (0 <= i <= n-2)，总满足 nums[i] <= nums[i + 1]。

双指针

• 双指针技巧汇总
• 一个函数秒杀 2Sum 3Sum 4Sum 问题

快慢指针——快排的基操

• 27. 移除元素

  给你一个数组 nums 和一个值 val，你需要 原地 移除所有数值等于 val 的元素，并返回移除后数组的新长度。

  不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并 原地 修改输入数组。

  元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

  class Solution { public: int removeElement(vector<int>& nums, int val) { //使用快慢指针 int fast =0; int slow = 0; int n = nums.size(); while(fast<n){ if(nums[fast]!=val){ nums[slow]=nums[fast];//其实应该是交换的，但没必要 ++slow; } ++fast; } return slow; } };

• 287. 寻找重复数

  给定一个包含 n + 1 个整数的数组 nums ，其数字都在 [1, n] 范围内（包括 1 和 n），可知至少存在一个重复的整数。

  假设 nums 只有 一个重复的整数 ，返回 这个重复的数 。

  你设计的解决方案必须 不修改 数组 nums 且只用常量级 O(1) 的额外空间。

  • 1 2	输入：nums = [1,3,4,2,2] 输出：2

  • 思路：二分查找和快慢指针。因为要用常量级空间，不能用哈希。

  • 思路1：数组进行映射，成为链表，即存在环，见下图。

  • 

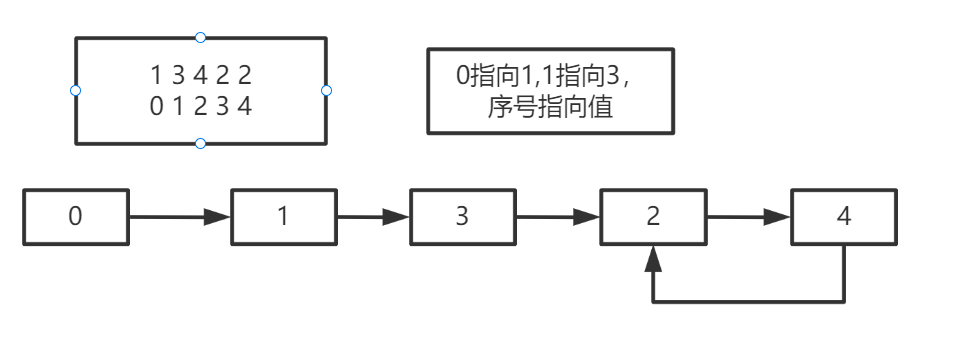
  • 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35

    class Solution { public: int findDuplicate(vector<int>& nums) { //暴力解法，超时 // int n=nums.size(); // int left=0,right=1; // while(left<n){ // while(right<n){ // if(nums[left]==nums[right]){ // return nums[left]; // } // ++right; // } // ++left; // right=left+1; // } // return nums[left]; // floy快慢指针 int slow=0,fast=0; do{ fast=nums[nums[fast]]; slow=nums[slow]; }while(slow!=fast); fast=0; while(fast!=slow){ fast=nums[fast]; slow=nums[slow]; } return slow; } };

  • 思路二：定义cnt[i] 表示 nums数组中小于等于i的数有多少个，i从1开始算起，使用二分法查找第一个大于cnt[i] >i的，i即为所求的重复数。

  • 

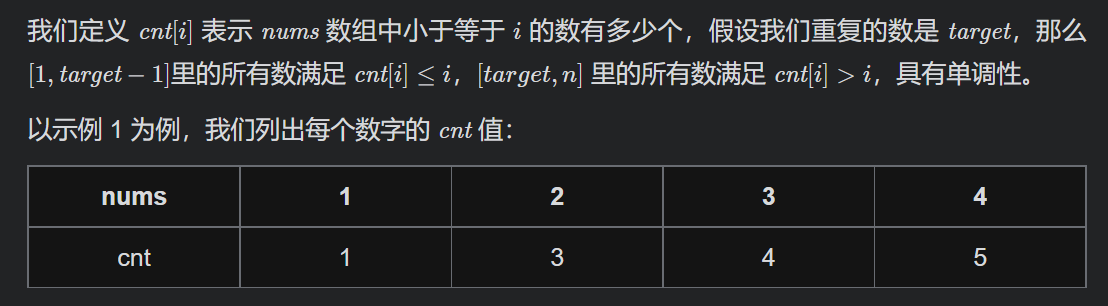
  • 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27

    class Solution { public: int findDuplicate(vector<int>& nums) { //二分查找 int n=nums.size(); int left=1,right=n-1; int ret=-1; //左闭右闭区间 while(left<=right){ int mid=left+(right-left)/2; //计算cnt int count=0; for(int i=0;i<n;++i){ if(nums[i]<=mid){ ++count; } } if(count<=mid){ left=mid+1; }else{ right=mid-1; ret=mid; } } return ret; } };

• 1861. 旋转盒子

  给你一个 m x n 的字符矩阵 box ，它表示一个箱子的侧视图。箱子的每一个格子可能为：

  • '#' 表示石头
  • '*' 表示固定的障碍物
  • '.' 表示空位置

  这个箱子被 顺时针旋转 90 度 ，由于重力原因，部分石头的位置会发生改变。每个石头会垂直掉落，直到它遇到障碍物，另一个石头或者箱子的底部。重力 不会 影响障碍物的位置，同时箱子旋转不会产生惯性 ，也就是说石头的水平位置不会发生改变。

  题目保证初始时 box 中的石头要么在一个障碍物上，要么在另一个石头上，要么在箱子的底部。

  请你返回一个 n x m的矩阵，表示按照上述旋转后，箱子内的结果

• 思路1：原地交换，利用双指针，一个指向障碍的底部，一个指向石头。注意点在于不要数组越界。先移动矩阵，再旋转矩阵。

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47

  class Solution { public: void ReSort(vector<char> &src,int cols){ int pred = cols-1; int stop = cols-1; while(stop>=0){ if(src[stop]!='.') --stop; else break; } pred = stop-1; while(pred>=0 && stop>=0){ if(pred>=0 && src[pred]=='#'){ swap(src[pred],src[stop]); --stop; --pred; } //重新确定边界 else if(pred>=1 && src[pred]=='*'){ stop = pred-1; while(stop>=0){ if(src[stop]!='.') --stop; else break; } pred = stop-1; }else{ --pred; } } } vector<vector<char>> rotateTheBox(vector<vector<char>>& box) { int rows = box.size(); int cols = box[0].size(); for(int i =0 ;i<rows;++i){ ReSort(box[i], cols); } vector<vector<char>> ret(cols,vector<char>(rows)); for(int i = 0;i<cols;++i){ for(int j = rows-1;j>=0;--j){ ret[i][rows-j-1] = box[j][i]; } } return ret; } };

• 思路2：由于重力向下，那么我们应当从右向左遍历原先的「每一行」。

  我们使用一个队列来存放一行中的空位：

  1.当我们遍历到一块石头时，就从队首取出一个空位来放置这块石头。如果队列为空，那么说明右侧没有空位，这块石头不会下落；

  2.当我们遍历到一个空位时，我们将其加入队列；

  3.当我们遍历到一个障碍物时，需要将队列清空，障碍物右侧的空位都是不可用的。

  在遍历完所有的行后，我们将矩阵顺时针旋转 90 度，放入答案数组中即可。

• 1229. 安排会议日程

  给定两个人的空闲时间表：slots1 和 slots2，以及会议的预计持续时间 duration，请你为他们安排 时间段最早 且合适的会议时间。

  如果没有满足要求的会议时间，就请返回一个 空数组。

  「空闲时间」的格式是 [start, end]，由开始时间 start 和结束时间 end 组成，表示从 start 开始，到 end 结束。

  题目保证数据有效：同一个人的空闲时间不会出现交叠的情况，也就是说，对于同一个人的两个空闲时间 [start1, end1] 和 [start2, end2]，要么 start1 > end2，要么 start2 > end1。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44

  class Solution { public: vector<int> minAvailableDuration(vector<vector<int>>& slots1, vector<vector<int>>& slots2, int duration) { //先排序 sort(slots1.begin(),slots1.end(),[](auto &i, auto &j)->bool{ return i[1]<j[1]; }); sort(slots2.begin(),slots2.end(),[](auto &i, auto &j)->bool{ return i[1]<j[1]; }); //假设已经拍好序 int n1=slots1.size(); int n2=slots2.size(); int ptr1=0,ptr2=0; vector<int> temp1,temp2; while(ptr1<n1 && ptr2<n2){ temp1=slots1[ptr1]; temp2=slots2[ptr2]; if(temp1[1]<=temp2[0]){ ++ptr1; }else if(temp1[0]>=temp2[1]){ ++ptr2; }else{ int left=max(temp1[0],temp2[0]); int right=min(temp1[1],temp2[1]); if((right-left)>=duration){ return vector<int>{left,left+duration}; }else{ if(temp1[1]>temp2[1]){ ++ptr2; }else if(temp1[1]<temp2[1]){ ++ptr1; }else{ ++ptr1; ++ptr2; } } } } return vector<int>{}; } };

• 283. 移动零

  给定一个数组给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

  • 必须在原数组上操作，不能拷贝额外的数组。

  • 尽量减少操作次数。

  • 算法1：直接采用非零删除，最后加零即可

  • 算法2：采用双指针，右指针一直循环，当不等于0时，交换左右指针的值，同时左指针+1。

    

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

  class Solution { public: void moveZeroes(vector<int>& nums) { int n=nums.size(); int left=0,right=0; while(right<n){ if(nums[right]!=0){ swap(nums[left],nums[right]); ++left; } //右指针一直循环 ++right; } } };

• 344. 反转字符串

  编写一个函数，其作用是将输入的字符串反转过来。输入字符串以字符数组 s 的形式给出。

  不要给另外的数组分配额外的空间，你必须**原地修改输入数组**、使用 O(1) 的额外空间解决这一问题。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

  //思路：双指针即可，同时移动 class Solution { public: void reverseString(vector<char>& s) { int n=s.size(); int left=0; int right=n-1; while(left<right){ char temp=s[left]; s[left]=s[right]; s[right]=temp; ++left; --right; } } };

• 19. 删除链表的倒数第 N 个结点

  给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34

  /** * Definition for singly-linked list. * struct ListNode { * int val; * ListNode *next; * ListNode() : val(0), next(nullptr) {} * ListNode(int x) : val(x), next(nullptr) {} * ListNode(int x, ListNode *next) : val(x), next(next) {} * }; */ class Solution { public: ListNode* removeNthFromEnd(ListNode* head, int n) { //查找倒数n个节点 ListNode *first=head; ListNode *second=head; for(int i=0;i<n;++i){ second=second->next; } //判断是的链表头 if(!second){ ListNode * ret=first->next; first->next=nullptr; return ret; } while(second->next){ second=second->next; first=first->next; } first->next=first->next->next; return head; } };

• 977. 有序数组的平方

  给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35

  class Solution { public: vector<int> sortedSquares(vector<int>& nums) { int n=nums.size(); vector<int> ret; int left=0; int right=n-1; //均为正数 if(nums[left]>=0){ for(auto &i:nums){ ret.emplace_back(i*i); } }else if(nums[right]<=0){ for(int i=right;i>=0;--i){ ret.emplace_back(nums[i]*nums[i]); } }else{ //双指针插入 while(left<=right){ int temp1=nums[left]*nums[left]; int temp2=nums[right]*nums[right]; if(temp1>temp2){ ret.emplace_back(temp1); ++left; }else{ ret.emplace_back(temp2); --right; } } //反转，原本是从大到小的 reverse(ret.begin(),ret.end()); } return ret; } };

• 167. 两数之和 II - 输入有序数组

  给定一个已按照 非递减顺序排列 的整数数组 numbers ，请你从数组中找出两个数满足相加之和等于目标数 target 。

  函数应该以长度为 2 的整数数组的形式返回这两个数的下标值*。*numbers 的下标 从 1 开始计数 ，所以答案数组应当满足 1 <= answer[0] < answer[1] <= numbers.length 。

  你可以假设每个输入 只对应唯一的答案 ，而且你 不可以 重复使用相同的元素。

• 88 合并两个有序数组

• 给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2，另有两个整数 m 和 n ，分别表示 nums1 和 nums2 中的元素数目。

  请你 合并 nums2 到 nums1 中，使合并后的数组同样按 非递减顺序 排列。

  注意：最终，合并后数组不应由函数返回，而是存储在数组 nums1 中。为了应对这种情况，nums1 的初始长度为 m + n，其中前 m 个元素表示应合并的元素，后 n 个元素为 0 ，应忽略。nums2 的长度为 n 。

• 142 环形链表

• 给定一个链表，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

  如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

  不允许修改 链表。

• 

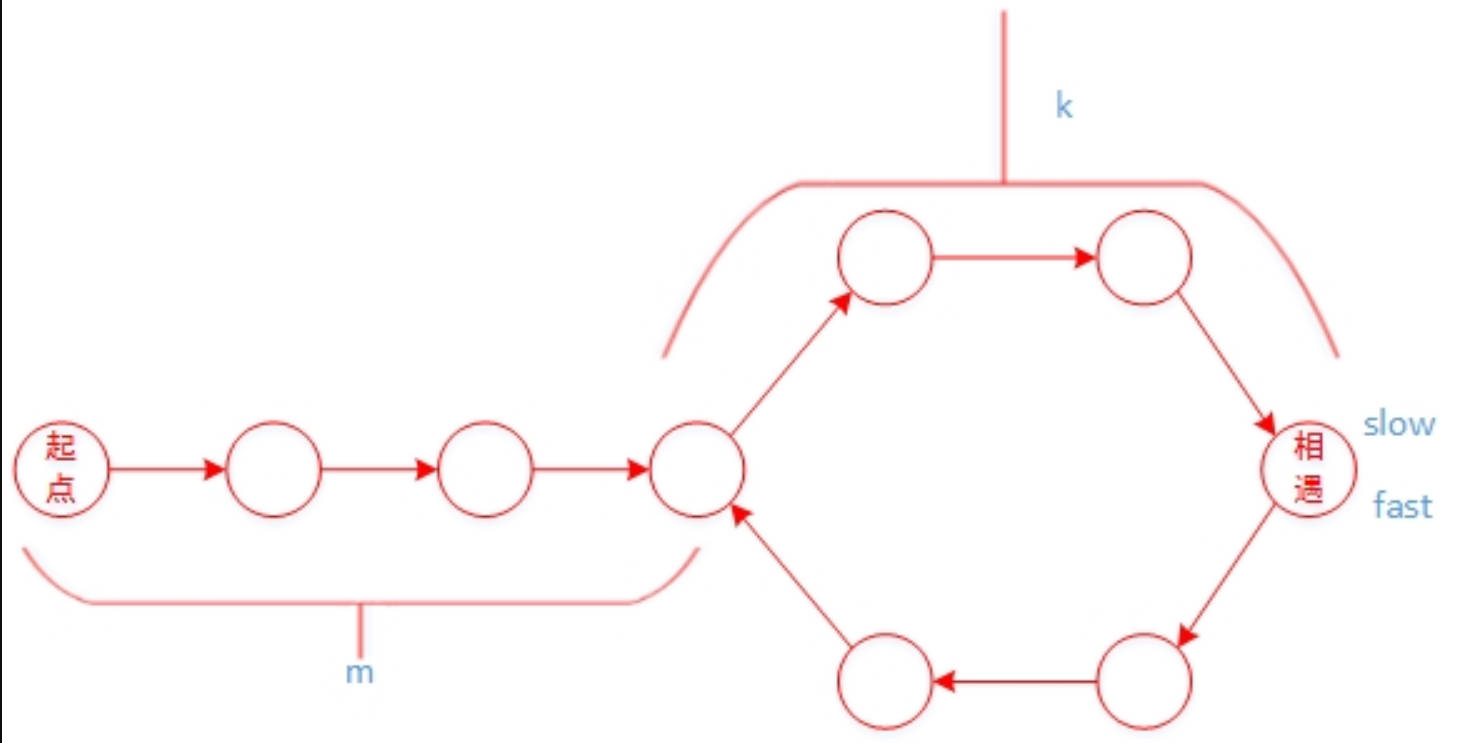
  • 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

    /* S=m+A*n+k 2S=m+B*n+k 相减 S=n*c（即是圈数的整数倍） 所以，d*n-k=m m可以是d圈再多一点，所以才有s=n*c 所以把fast放在head，同步slow和fast，再次相遇可以找到环的起点 */ /*对于链表找环路的问题，有一个通用的解法——快慢指针（Floyd 判圈法）。给定两个指针， 分别命名为 slow 和 fast，起始位置在链表的开头。每次 fast 前进两步，slow 前进一步。如果 fast 可以走到尽头，那么说明没有环路；如果 fast 可以无限走下去，那么说明一定有环路，且一定存 在一个时刻 slow 和 fast 相遇。当 slow 和 fast 第一次相遇时，我们将 fast 重新移动到链表开头，并 让 slow 和 fast 每次都前进一步。当 slow 和 fast 第二次相遇时，相遇的节点即为环路的开始点。 */

  • 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

    /** * Definition for singly-linked list. * struct ListNode { * int val; * ListNode *next; * ListNode(int x) : val(x), next(NULL) {} * }; */ class Solution { public: ListNode *detectCycle(ListNode *head) { //判断有环,使用do while先走一遍 ListNode *fast=head; ListNode *slow=head; do{ if(!fast||!fast->next) return nullptr; fast=fast->next->next; slow=slow->next; }while(fast!=slow); //返回起点 fast=head; while(fast!=slow){ fast=fast->next; slow=slow->next; } return fast; } };

• 82. 删除排序链表中的重复元素 II

  存在一个按升序排列的链表，给你这个链表的头节点 head ，请你删除链表中所有存在数字重复情况的节点，只保留原始链表中 没有重复出现 的数字。

  返回同样按升序排列的结果链表。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38

  /** * Definition for singly-linked list. * struct ListNode { * int val; * ListNode *next; * ListNode() : val(0), next(nullptr) {} * ListNode(int x) : val(x), next(nullptr) {} * ListNode(int x, ListNode *next) : val(x), next(next) {} * }; */ class Solution { public: ListNode* deleteDuplicates(ListNode* head) { if(!head){ return head; } //创建哑巴节点，防止11 22 33开头即重复 ListNode *dummyHead=new ListNode(-101,head); ListNode *pre=dummyHead; ListNode *cur=dummyHead->next; while(cur &&cur->next){ if(cur->val==cur->next->val){ //保存变量 int x=cur->val; //一直找下一个指针 while(cur&&cur->val==x){ cur=cur->next; } pre->next=cur; }else{ //都往前移动 pre=cur; cur=cur->next; } } return dummyHead->next; } };

• 15. 三数之和

  给你一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 *a，b，c ，*使得 a + b + c = 0 ？请你找出所有和为 0 且不重复的三元组。

  **注意：**答案中不可以包含重复的三元组。

  • 使用dfs回溯，但是超时

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42

  vector<vector<int>> ret; vector<int> path; void backtracking(vector<int>& nums,int sum, int target,int start){ if(path.size()==3&&sum==target){ ret.push_back(path); return; } if(sum>target){ return; } if(path.size()>3){ return; } for(int i=start;i<nums.size();++i){ //去重操作，树的横向遍历,注意是大于start，不是大于0，以此保证第一个数可以插入 if(i>start&&nums[i]==nums[i-1]){ continue; } path.push_back(nums[i]); sum+=nums[i]; //递归 backtracking(nums, sum, target, i+1); //回溯 path.pop_back(); sum-=nums[i]; } } vector<vector<int>> threeSum(vector<int>& nums) { //先排序防止重复 sort(nums.begin(),nums.end()); int n=nums.size(); path.clear(); ret.clear(); int sum=0; backtracking(nums, sum, 0, 0); return ret; }

  • 使用双指针，缩减为twosum问题

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59

  class Solution { public: //思路1：采用dfs穷举 //思路2：采用twosum双指针 vector<vector<int>> twosum(vector<int>& nums,int start,int target){ int left=start; int right=nums.size()-1; vector<vector<int>> ret; while(left<right){ int sum=nums[left]+nums[right]; if(sum>target){ --right; }else if(sum<target){ ++left; } else{ vector<int> temp{nums[left],nums[right]}; ret.push_back(temp); //防止重复 while(left<right&&nums[left+1]==nums[left]){ ++left; } while(left<right&&nums[right]==nums[right-1]){ --right; } ++left; --right; } } return ret; } vector<vector<int>> threeSum(vector<int>& nums) { //先排序防止重复 sort(nums.begin(),nums.end()); int n=nums.size(); vector<vector<int>> ret; if(n<3){ return ret; }else{ int i=0; while(i<n-2){ vector<vector<int>> temp; temp=twosum(nums, i+1, 0-nums[i]); for(auto &j:temp){ j.push_back(nums[i]); ret.emplace_back(j); } //防止重复 while(i+1<n-2&&nums[i]==nums[i+1]){ ++i; } ++i; } } return ret; } };

• 844. 比较含退格的字符串

  给定 s 和 t 两个字符串，当它们分别被输入到空白的文本编辑器后，请你判断二者是否相等。# 代表退格字符。

  如果相等，返回 true ；否则，返回 false 。

  注意：如果对空文本输入退格字符，文本继续为空。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90

  class Solution { public: bool backspaceCompare(string s, string t) { // //思路1：直接得到最后的字符串进行比较 // int n1=s.size(); // int n2=t.size(); // string s1,t1; // for(int i=0;i<n1;++i){ // if(s[i]=='#'){ // if(s1.empty()){ // continue; // }else{ // s1.pop_back(); // } // }else{ // s1.push_back(s[i]); // } // } // for(int i=0;i<n2;++i){ // if(t[i]=='#'){ // if(t1.empty()){ // continue; // }else{ // t1.pop_back(); // } // }else{ // t1.push_back(t[i]); // } // } // if(s1==t1){ // return true; // } // return false; //思路2：双指针进行逆序比较 int n1=s.size(); int n2=t.size(); int skipS=0; int skipT=0; int pointS=n1-1; int pointT=n2-1; //注意while循环一定是或，不是与，否则缺少一种判断false的情况 while(pointS>=0||pointT>=0){ //统计s的# while(pointS>=0){ if(s[pointS]=='#'){ skipS++; --pointS; }else{ if(skipS>0){ --pointS; skipS--; }else{ //指向非#号字符 break; } } } //统计t的# while(pointT>=0){ if(t[pointT]=='#'){ skipT++; --pointT; }else{ if(skipT>0){ --pointT; skipT--; }else{ //指向非#号字符 break; } } } if(pointS>=0&&pointT>=0){ if(s[pointS]!=t[pointT]){ return false; } }else{ //因为已经指向非#字符了，如果有一个存在，另外一个不存在，那么就不等 //只有都不存在，才符合 if(pointS>=0||pointT>=0){ return false; } } --pointS; --pointT; } return true; } };

• 986. 区间列表的交集

  给定两个由一些 闭区间 组成的列表，firstList 和 secondList ，其中 firstList[i] = [starti, endi] 而 secondList[j] = [startj, endj] 。每个区间列表都是成对 不相交 的，并且 已经排序 。

  返回这 两个区间列表的交集 。

  形式上，闭区间 [a, b]（其中 a <= b）表示实数 x 的集合，而 a <= x <= b 。

  两个闭区间的 交集 是一组实数，要么为空集，要么为闭区间。例如，[1, 3] 和 [2, 4] 的交集为 [2, 3] 。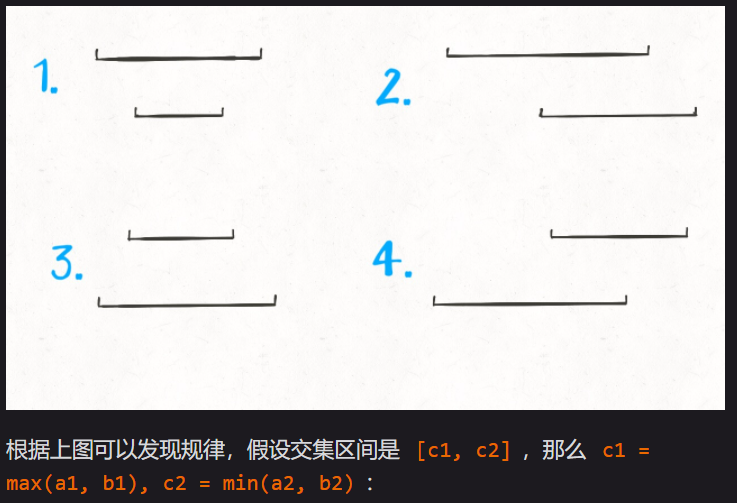

  

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46

  class Solution { public: vector<vector<int>> ret; vector<vector<int>> intervalIntersection(vector<vector<int>>& firstList, vector<vector<int>>& secondList) { int n1=firstList.size(); int n2=secondList.size(); int fir=0;int sec=0; ret.clear(); while(fir<n1&&sec<n2){ int a1=firstList[fir][0]; int a2=firstList[fir][1]; int b1=secondList[sec][0]; int b2=secondList[sec][1]; // //存在交集的条件 // if(b2>=a1&&a2>=b1){ // vector<int> temp{max(a1,b1),min(a2,b2)}; // ret.emplace_back(temp); // if(b2>a2){ // ++fir; // }else{ // ++sec; // } // } // else{ // if(a1>b2){ // ++sec; // }else if(a2<b1){ // ++fir; // } // } //优化的点：if条件可以合并 //存在交集的条件 if(b2>=a1&&a2>=b1){ vector<int> temp{max(a1,b1),min(a2,b2)}; ret.emplace_back(temp); } if(a2>b2){ ++sec; }else{ ++fir; } } return ret; } };

高频面试题之盛水容器和接雨水

• 11. 盛最多水的容器思路

  给你 n 个非负整数 a1，a2，...，a``n，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0) 。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

  说明: 你不能倾斜容器。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35

  class Solution { public: int maxArea(vector<int>& height) { //暴力解法，超时 // int n=height.size(); // int left=0; // int right=left+1; // int ret=0; // while(left<n-1){ // while(right<n){ // ret=max(ret,min(height[left],height[right])*(right-left)); // ++right; // } // ++left; // right=left+1; // } // return ret; //优化：双指针，移动较小的高度，以期许获得更大的面积；移动较大的高度，一定会比现在的面积小 int left=0; int right=height.size()-1; int ret=0; while(left<right){ ret=max(ret,min(height[left],height[right])*(right-left)); if(height[left]<height[right]){ ++left; }else{ --right; } } return ret; } };

• 42. 接雨水

  给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。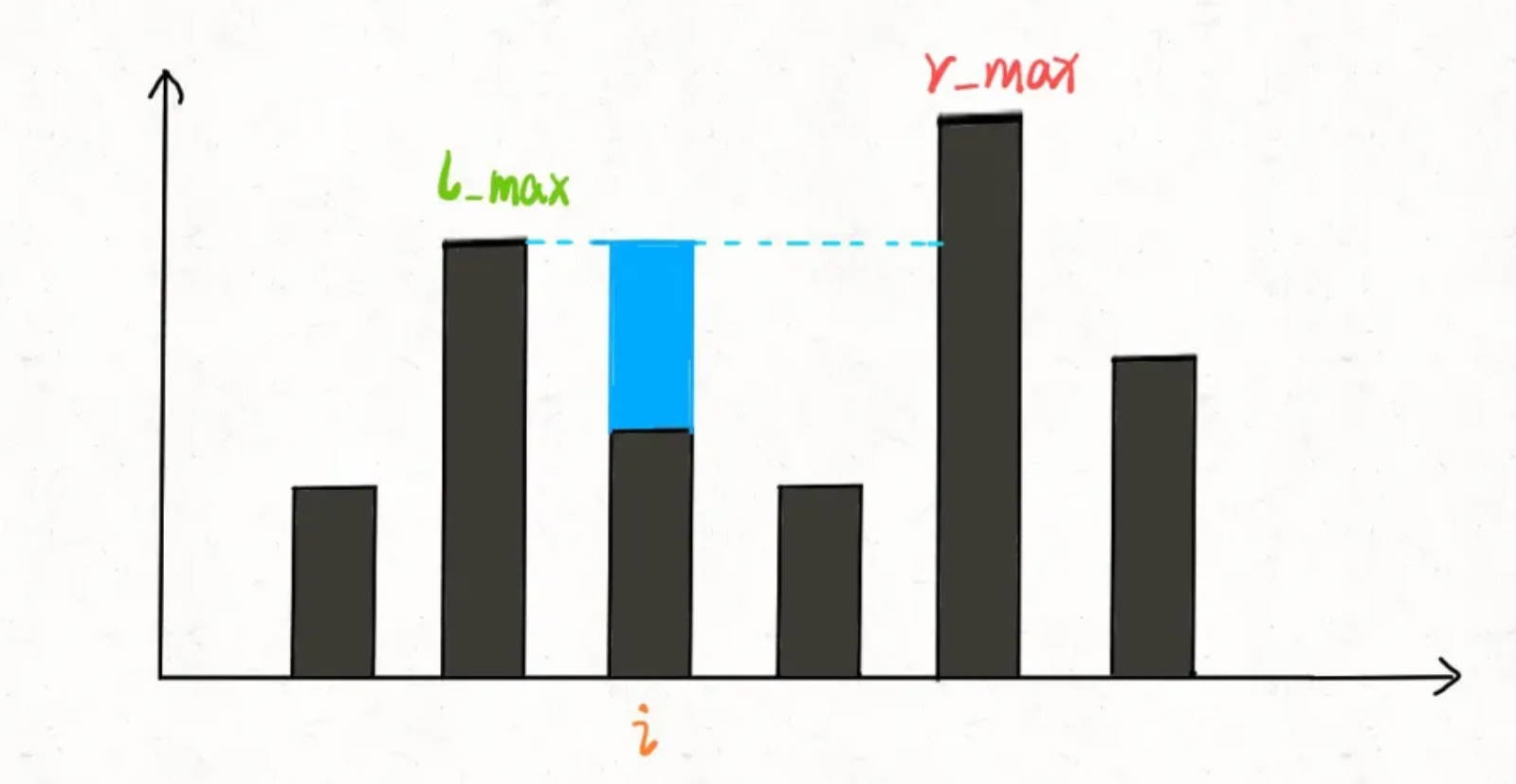

  

• 思路一：

  我们开两个数组r_max和l_max充当备忘录，l_max[i]表示位置i左边最高的柱子高度，r_max[i]表示位置i右边最高的柱子高度。预先把这两个数组计算好，避免重复计算。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34

  class Solution { public: int trap(vector<int>& height) { //方法一：备忘录。思考暴力解法，每根柱子最多接水为min(maxleft,maxright)-height int n=height.size(); if(n<=1){ return 0; } vector<int> maxleft(n); vector<int> maxright(n); int left_flag=height[0]; maxleft[0]=height[0]; for(int i=1;i<n;++i){ left_flag=max(left_flag,height[i]); maxleft[i]=left_flag; } int right_flag=height[n-1]; maxright[n-1]=height[n-1]; for(int i=n-2;i>=0;--i){ right_flag=max(right_flag,height[i]); maxright[i]=right_flag; } int ret=0; for(int i=0;i<n;++i){ int temp=min(maxleft[i],maxright[i])-height[i]; if(temp<0){ temp=0; } ret+=temp; } return ret; } };

• 思路二：双指针法

  

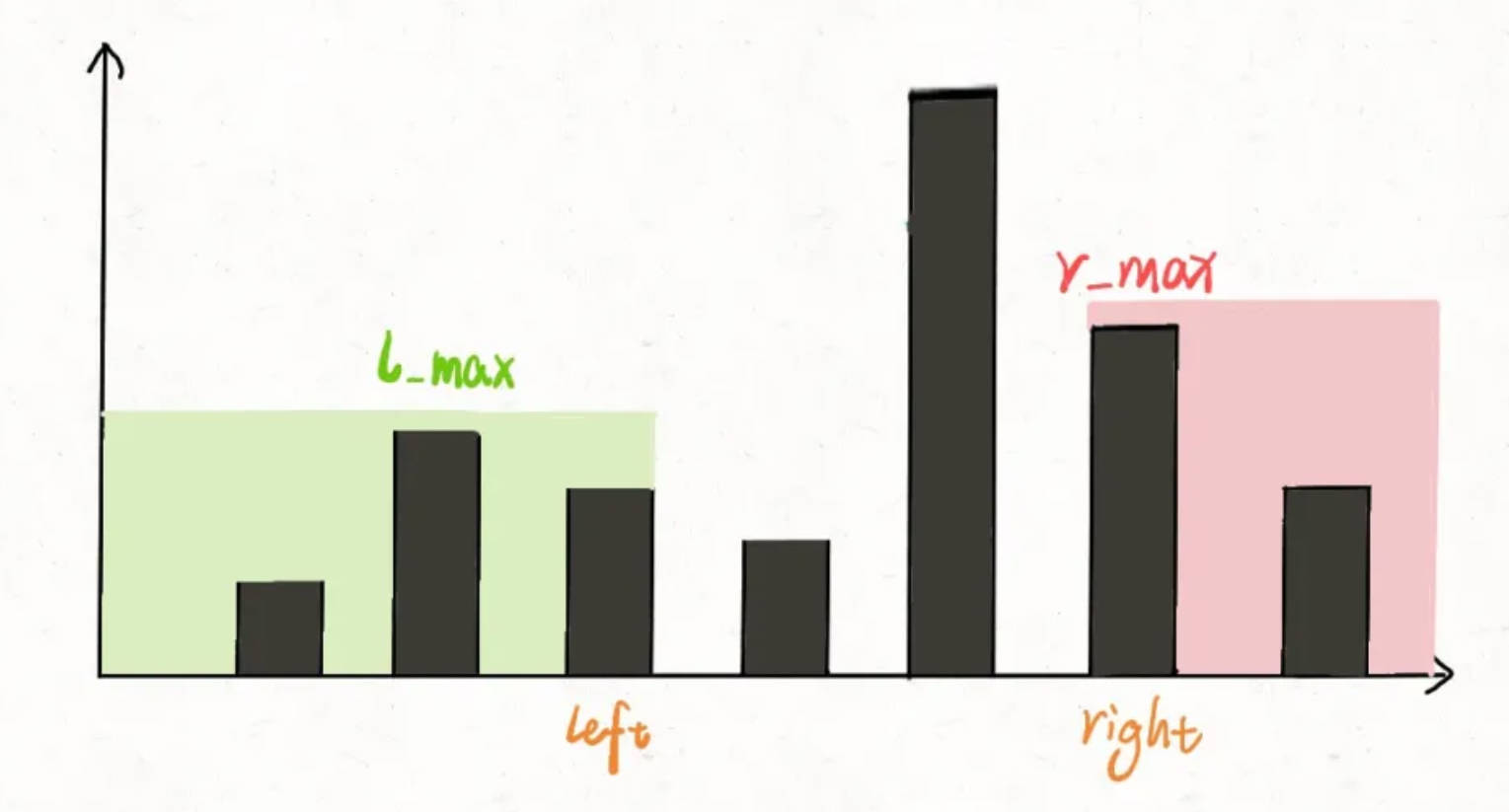
  我们只在乎min(l_max, r_max)。对于上图的情况，我们已经知道l_max < r_max了，至于这个r_max是不是右边最大的，不重要。重要的是height[i]能够装的水只和较低的l_max之差有关。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29

  class Solution { public: int trap(vector<int>& height) { //双指针法 int n=height.size(); if(n<=1){ return 0; } //left_flag是height[0left]中最高柱子的高度，right_flag是height[rightend]的最高柱子的高度。 int left=0; int right=n-1; int ret=0; int left_flag=height[0]; int right_flag=height[n-1]; while(left<right){ left_flag=max(height[left],left_flag); right_flag=max(height[right],right_flag); //移动小的一边，因为小的一边已经是确定了的可接水的容量，不关心大的一边是不是真的最大。 if(left_flag<right_flag){ ret+=left_flag-height[left]; ++left; }else{ ret+=right_flag-height[right]; --right; } } return ret; } };

• 1868. 两个行程编码数组的积

  行程编码 （Run-length encoding） 是一种压缩算法，能让一个含有许多段连续重复数字的整数类型数组 nums 以一个（通常更小的）二维数组 encoded 表示。每个 encoded[i] = [vali, freqi] 表示 nums 中第 i 段重复数字，其中 vali 是该段重复数字，重复了 freqi 次。

  • 例如， nums = [1,1,1,2,2,2,2,2] 可表示称行程编码数组 encoded = [[1,3],[2,5]] 。对此数组的另一种读法是“三个 1 ，后面有五个 2 ”。

  两个行程编码数组 encoded1 和 encoded2 的积可以按下列步骤计算：

  1. 将 encoded1 和 encoded2 分别扩展成完整数组 nums1 和 nums2 。
  2. 创建一个新的数组 prodNums ，长度为 nums1.length 并设 prodNums[i] = nums1[i] * nums2[i] 。
  3. 将 prodNums 压缩成一个行程编码数组并返回之。

  给定两个行程编码数组 encoded1 和 encoded2 ，分别表示完整数组 nums1 和 nums2 。nums1 和 nums2 的长度相同。 每一个 encoded1[i] = [vali, freqi] 表示 nums1 中的第 i 段，每一个 encoded2[j] = [valj, freqj] 表示 nums2 中的第 j 段。

  返回 encoded1 和 encoded2 的乘积。

  注：行程编码数组需压缩成可能的最小长度。

  • 思路：暴力破解时间复杂度过高，使用双指针，难点在于原地修改数组，这样可以避免一系列判断。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32

  class Solution { public: vector<vector<int>> findRLEArray(vector<vector<int>>& encoded1, vector<vector<int>>& encoded2) { int n1=encoded1.size(); int n2=encoded2.size(); int i=0,j=0; vector<vector<int>> ret; //直接原地修改，就不用新加其他的判断了 while(i<n1 && j<n2){ int sum=encoded1[i][0]*encoded2[j][0]; int len=min(encoded1[i][1],encoded2[j][1]); vector<int> curr{sum,len}; //原地修改 encoded1[i][1]-=len; encoded2[j][1]-=len; //考虑和前一个相等，需要合并 if(!ret.empty() && ret.back()[0]==sum){ ret.back()[1]+=len; }else{ ret.emplace_back(curr); } //更新指针 if(encoded1[i][1]==0){ ++i; } if(encoded2[j][1]==0){ ++j; } } return ret; } };

滑动窗口

• 代码套路

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28

  /* 滑动窗口算法框架 */ //一些前提，判断函数等等 void slidingWindow(string s, string t) { unordered_map<char, int> need, window; for (char c : t) need[c]++; int left = 0, right = 0; while (right < s.size()) { // c 是将移入窗口的字符 char c = s[right]; ++right; // 进行窗口内数据的一系列更新 ... // 判断左侧窗口是否要收缩 while (window needs shrink) { // d 是将移出窗口的字符 char d = s[left]; // 左移窗口 ++left; // 进行窗口内数据的一系列更新 ... } } }

单调队列和优先队列

• 顾名思义，所谓单调队列，那么其中的元素从队头到队尾一定要具有单调性（单调升、单调降等）。它被广泛地用于“滑动窗口”这一类RMQ问题，其功能是O(n)的维护整个序列中长度为k的区间最大值或最小值。

• 使用deque维护单调队列。

• 优先队列有另一个名字：二叉堆。功能是维护一堆数的最大值（大根堆）/最小值（小根堆），存放在堆顶（也就是根）。

• 使用priority_queue作为优先队列

• 239. 滑动窗口最大值

  给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

  返回 滑动窗口中的最大值 。

  • 一般这种题目都是使用单调队列或者优先队列。

  • 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

    //使用优先队列，默认大顶堆，注意添加位置！！ class Solution { public: vector<int> maxSlidingWindow(vector<int>& nums, int k) { int n=nums.size(); vector<int> ret; priority_queue<pair<int,int>> dp; //一个数值，一个是位置 for(int i=0;i<k;++i){ // dp.emplace(nums[i],i); dp.push(pair<int,int>{nums[i],i}); } ret.emplace_back(dp.top().first); int right=k; while(right<n){ dp.push(pair<int,int>{nums[right],right}); while(dp.top().second<=(right-k)){ dp.pop(); } ret.emplace_back(dp.top().first); ++right; } return ret; } };

  • 使用deque双头队列维持单调队列，队列元素的是数组的值的位置，不断加入，但是肯定比前面的位置大，满足单调队列的性质。

  • 当滑动窗口向右移动时，我们需要把一个新的元素放入队列中。为了保持队列的性质，我们会不断地将新的元素与队尾的元素相比较，如果前者大于等于后者，那么队尾的元素就可以被永久地移除，我们将其弹出队列。我们需要不断地进行此项操作，直到队列为空或者新的元素小于队尾的元素。

  • 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31

    class Solution { public: vector<int> maxSlidingWindow(vector<int>& nums, int k) { int n=nums.size(); deque<int> dp; for(int i=0;i<k;++i){ //等于也删除，更新最大的位置,一直维护单调队列 while(!dp.empty() &&nums[dp.back()]<=nums[i]){ dp.pop_back(); } dp.push_back(i); } vector<int> ret; ret.push_back(nums[dp.front()]); int right=k; while(right<n){ //等于也删除，更新最大的位置 while(!dp.empty() &&nums[dp.back()]<=nums[right]){ dp.pop_back(); } dp.push_back(right); //判断左边 while(dp.front()<=(right-k)){ dp.pop_front(); } ret.push_back(nums[dp.front()]); ++right; } return ret; } };

• 1004. 最大连续1的个数 III

  给定一个二进制数组 nums 和一个整数 k ，如果可以翻转最多k 个 0 ，则返回 数组中连续 1 的最大个数 。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27

  class Solution { public: int longestOnes(vector<int>& nums, int k) { int n=nums.size(); int left=0; int right=0; int ret=0; int count=0; while(right<n){ if(nums[right]==0){ ++count; } if(count>k){ ret=max(ret,right-left); } while(count>k){ if(nums[left]==0){ --count; } ++left; } ret=max(ret,right-left+1); ++right; } return ret; } };

• 159. 至多包含两个不同字符的最长子串

  给定一个字符串 *s* ，找出 至多 包含两个不同字符的最长子串 *t* ，并返回该子串的长度。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48

  class Solution { public: int lengthOfLongestSubstringTwoDistinct(string s) { int n=s.size(); unordered_map<char,int> need; int left=0,right=0; int ret=0; while(right<n){ //更新窗口 char temp=s[right]; need[temp]++; //收缩窗口 //计算第一次ret if(need.size()>2){ // int sum=0; // for(auto &i:need){ // if(i.first!=temp){ // sum+=i.second; // } // } // ret=max(ret,sum); //直接左右指针相减就是了 ret=max(ret,(right-left)); } while(need.size()>2&&left<=right){ char temp1=s[left]; need[temp1]--; //判断是否删除，即使等于0还是有 if(need[temp1]==0){ need.erase(temp1); } ++left; } // //计算第二次ret // int sum1=0; // for(auto &i:need){ // sum1+=i.second; // } // ret=max(ret,sum1); ret=max(ret,right-left+1); ++right; } return ret; } };

• 340. 至多包含 K 个不同字符的最长子串

  给定一个字符串 *s* ，找出 至多 包含 k 个不同字符的最长子串 *T*。

  • 思路：和T159思路很类似。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

  class Solution { public: int lengthOfLongestSubstringKDistinct(string s, int k) { int n=s.size(); unordered_map<char,int> window; int ret=0; int left=0,right=0; while(right<n){ char temp1=s[right]; window[temp1]++; //计算第一次ret if(window.size()>k){ ret=max(ret,right-left); } while(window.size()>k&&left<=right){ char temp2=s[left]; window[temp2]--; if(window[temp2]==0){ window.erase(temp2); } ++left; } //计算第二次ret ret=max(ret,right-left+1); ++right; } return ret; } };

• 438. 找到字符串中所有字母异位词

  给定两个字符串 s 和 p，找到 s 中所有 p 的 异位词 的子串，返回这些子串的起始索引。不考虑答案输出的顺序。

  异位词 指由相同字母重排列形成的字符串（包括相同的字符串）。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47

  //记住模板，就可以做 class Solution { public: vector<int> findAnagrams(string s, string p) { unordered_map<char,int> need,window; int ns=s.size(); int np=p.size(); vector<int> ret; if(ns<np){ return ret; } //初始化need for(auto &i:p){ need[i]++; } int left=0; int right=0; int valid=0;//记住判断是否一致的参数 while(right<ns){ char c=s[right]; ++right; if(need.count(c)){ window[c]++; if(window[c]==need[c]){ ++valid; } } //窗口收缩 while((right-left)>=np){ //证明这个数组可以 if(valid==need.size()){ ret.push_back(left); } //收缩 char c=s[left]; ++left; if(window.count(c)){ if(window[c]==need[c]){ --valid; } window[c]--; } } } return ret; } };

• 713. 乘积小于K的子数组

  给定一个正整数数组 nums和整数 k 。

  请找出该数组内乘积小于 k 的连续的子数组的个数。

  • 思路：这道题不是典型滑动窗口题目，难道在于巧妙计算
  • 窗口左边界和右边界。一直移动右边界，当乘积小于k时，此时两个左右边界指针之间有多少个数字，就找到了多少个数字乘积小于k的子数组。当乘积大于等于k时候，移动左边界。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23

  class Solution { public: int numSubarrayProductLessThanK(vector<int>& nums, int k) { int n=nums.size(); int ret=0; int left=0; int right=0; long long sum=1; while(right<n){ sum=sum*nums[right]; ++right; //收缩窗口 while(right>left&&sum>=k){ sum/=nums[left]; ++left; } //左右指针之差即为子数组个数，如[1,5,7],可以有[157][57][7]三个子数组 ret+=right-left; } return ret; } };

• 209. 长度最小的子数组

  给定一个含有 n 个正整数的数组和一个正整数 target 。

  找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度**。**如果不存在符合条件的子数组，返回 0 。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

  class Solution { public: int minSubArrayLen(int target, vector<int>& nums) { int n=nums.size(); int left=0; int right=0; int sum=0; int ret=INT_MAX; while(right<n){ sum+=nums[right]; ++right; while(right>left&&sum>=target){ ret=min(ret,right-left); sum-=nums[left]; ++left; } } if(ret==INT_MAX){ ret=0; } return ret; } };

• 3. 无重复字符的最长子串

  给定一个字符串 s ，请你找出其中不含有重复字符的 最长子串 的长度

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33

  //思路：框架三步走，注意用unordered_map，定义字符在窗口中存在的个数。 class Solution { public: int lengthOfLongestSubstring(string s) { unordered_map<char,int> record; int n=s.size(); if(n==0){ return 0; } int left=0,right=0; int ret=0; while(right<n){ //1.更新右边 char c=s[right]; ++right; record[c]++;//更新窗口,映射数目+1 //2.更新左边 //判断收缩，一直循环 while(record[c]>1){ char d=s[left]; ++left; record[d]--;//更新窗口 } //3.更新答案 ret=max(ret,right-left); } return ret; } };

• 567. 字符串的排列

  给你两个字符串 s1 和 s2 ，写一个函数来判断 s2 是否包含 s1 的排列。如果是，返回 true ；否则，返回 false 。

  换句话说，s1 的排列之一是 s2 的 子串 。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88

  class Solution { public: //第一种方式超时 // bool checkInclusion(string s1, string s2) { // unordered_map<char,int> window; // unordered_map<char ,int> need; // for(auto &i:s1){ // window[i]++; // } // int n=s2.size(); // int n1=s1.size(); // if(n<n1){ // return false; // } // int left=0; // while(left<=n-n1){ // char c=s2[left]; // if(window[c]){ // need[c]++; // bool flag=true; // int i=1; // while(i<n1){ // char d=s2[left+i]; // if(window[d]){ // need[d]++; // if(need[d]>window[d]){ // flag=false; // break; // } // }else{ // flag=false; // break; // } // ++i; // } // if(flag){ // return true; // } // } // ++left; // need.clear(); // } // return false; //思路二：经典滑动窗口框架 bool checkInclusion(string s1, string s2) { unordered_map<char,int> window; unordered_map<char ,int> need; for(auto &i:s1){ need[i]++; } int left=0,right=0; int valid=0;//符合的字符数 int n2=s2.size(); int n1=s1.size(); while(right<n2){ char c=s2[right]; ++right; //更新窗口 if(need.count(c)){ //先添加，后判断 window[c]++; if(window[c]==need[c]){ ++valid; } } //判断是否收缩窗口 while(right-left>=n1){ //注意不是n2，而是哈希表的数目，因为有重复的情况 if(valid==need.size()){ return true; } char d=s2[left]; ++left; if(need.count(d)){ //先更新valid，后删除键值 if(window[d]==need[d]){ --valid; } window[d]--; } } } return false; } };

• 76. 最小覆盖子串 ——滑动窗口

  给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 "" 。

  注意：

  • 对于 t 中重复字符，我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
  • 如果 s 中存在这样的子串，我们保证它是唯一的答案。

• 输入：s = "ADOBECODEBANC", t = "ABC"
  输出："BANC"
  

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53

  class Solution { public: //定义两个哈希判断，因为没有顺序要求，只有数量要求 unordered_map<char,int> ori,dst; //判断是否包含函数 bool check(){ for(auto &p:ori){ if(dst[p.first]<p.second){//p.first是一个字符char return false; } } return true; } //s查找t string minWindow(string s, string t) { //初始化ori for(auto &c:t){ ++ori[c]; } //定义标志 int len=INT_MAX; int l=0,r=-1; int ansl=-1;//多加的标志 int ansr=-1; int siz_len=s.size(); while(++r<siz_len){ //!=即存在,先走完r if(ori.find(s[r])!=ori.end()){ ++dst[s[r]]; } while(check()&&l<=r){ //取最小长度 if(len>r-l+1){ ansl=l; ansr=r;//r=-1是最好的选择，这样就不用r-1，每次都指着这次的指针 len=r-l+1; } //l指针往前走，因为唯一，所以往前走要判断是否存在 if(ori.find(s[l])!=ori.end()){ --dst[s[l]];//当存在的时候要进一步减少，免得判断失败 } ++l; } } if(ansl==-1){ return string() ; }else{ return s.substr(ansl, len); } } };

• 633 平方数之和

• 给定一个非负整数 c ，你要判断是否存在两个整数 a 和 b，使得 a2 + b2 = c 。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32

  class Solution { public: bool judgeSquareSum(int c) { //双指针,本来是int，然后出错了，所以可以知道类型转换有时候出错，且耗时，最好都是高一级的 long i=0; long j=(long)sqrt(c); while(i<=j){ long sum1=i*i+j*j; if(sum1==c){ return true; }else if(sum1>c){ --j; }else{ ++i; } } return false; // long left = 0; // long right = (long) sqrt(c); // while (left <= right) { // long sum = left * left + right * right; // if (sum == c) { // return true; // } else if (sum > c) { // right--; // } else { // left++; // } // } // return false; } };

• 680. 验证回文字符串 Ⅱ

  给定一个非空字符串 s，最多删除一个字符。判断是否能成为回文字符串。

  • 若一个字符串的正序与倒序相同,则称其为回文字符串;

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33

  class Solution { public: bool check_valid(int left,int right,const string &s){ int i=left; int j=right; while(i<j){ if(s[i]!=s[j]){ return false; }else{ ++i; --j; } } return true; } bool validPalindrome(string s) { int i=0; int j=s.size()-1; while(i<j){ if(s[i]!=s[j]){ return (check_valid(i+1,j, s)) || (check_valid(i,j-1, s)); break; }else{ ++i; --j; } } return true; } };

• 524. 通过删除字母匹配到字典里最长单词

  给你一个字符串 s 和一个字符串数组 dictionary ，找出并返回 dictionary 中最长的字符串，该字符串可以通过删除 s 中的某些字符得到。

  如果答案不止一个，返回长度最长且字母序最小的字符串。如果答案不存在，则返回空字符串。

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51

  class Solution { public: //是否包含，双指针 bool check_include(const string &src,const string &dst,int len_r){ int i=0,j=0; int len_d=dst.size(); while(i<len_r&&j<len_d){ if(src[i]==dst[j]){ ++i; ++j; }else{ ++i; } } if(j==len_d) return true; else return false; } string findLongestWord(string s, vector<string>& dictionary) { int num=dictionary.size(); int siz=s.size(); int len=0;//不能写负数，因为size是无符号数，会自动转化 string out=string();//空字符串 for(int i=0;i<num;++i){ string temp=dictionary[i]; if(len<=temp.size()){ if(check_include(s, temp, siz)){ if(len<temp.size()){ len=temp.size(); out=temp; }else{ //相同字长取最小字母序 for(int te=0;te<temp.size();++te){ if(out[te]<temp[te]){ break; } else if(out[te]>temp[te]){ out=temp; break; } } } } } } return out; } };

二叉树

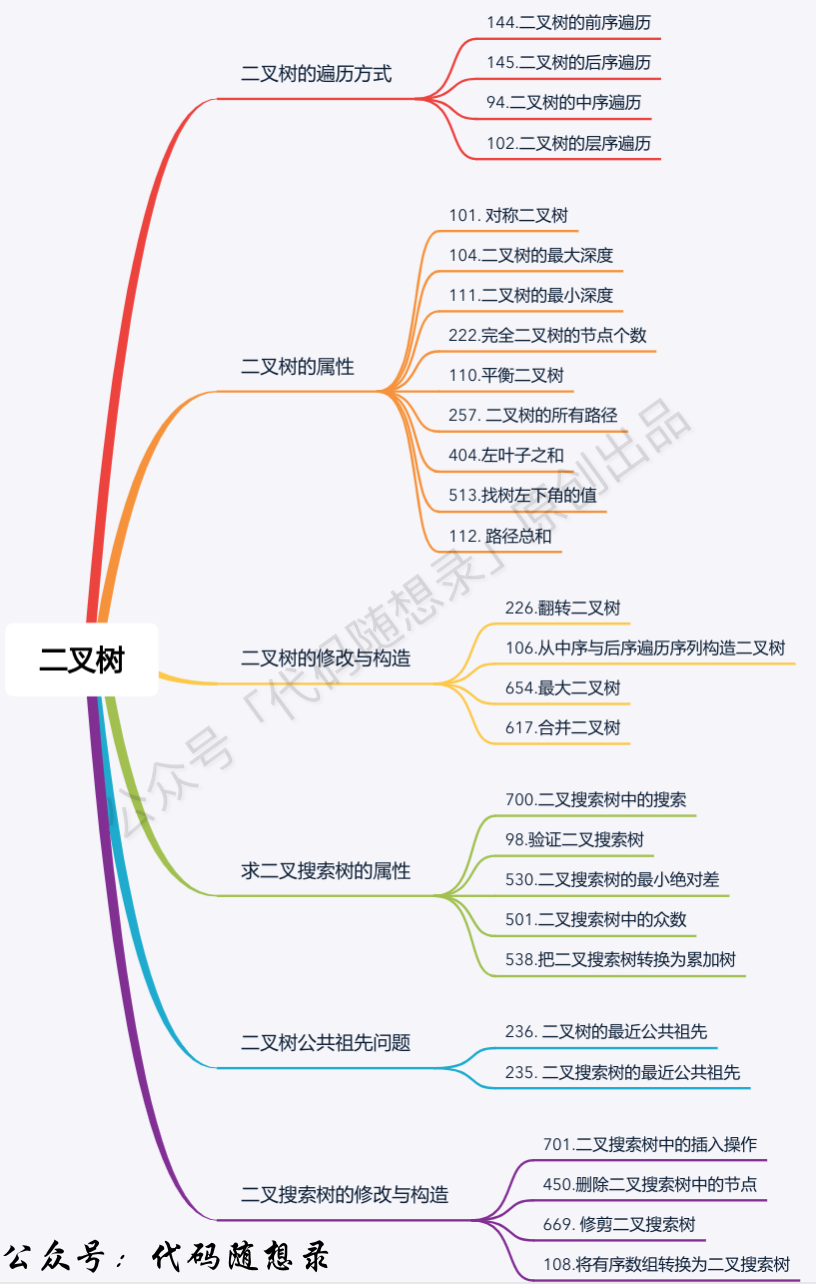
基本理论

• 满二叉树：所有节点都是满的

  满二叉树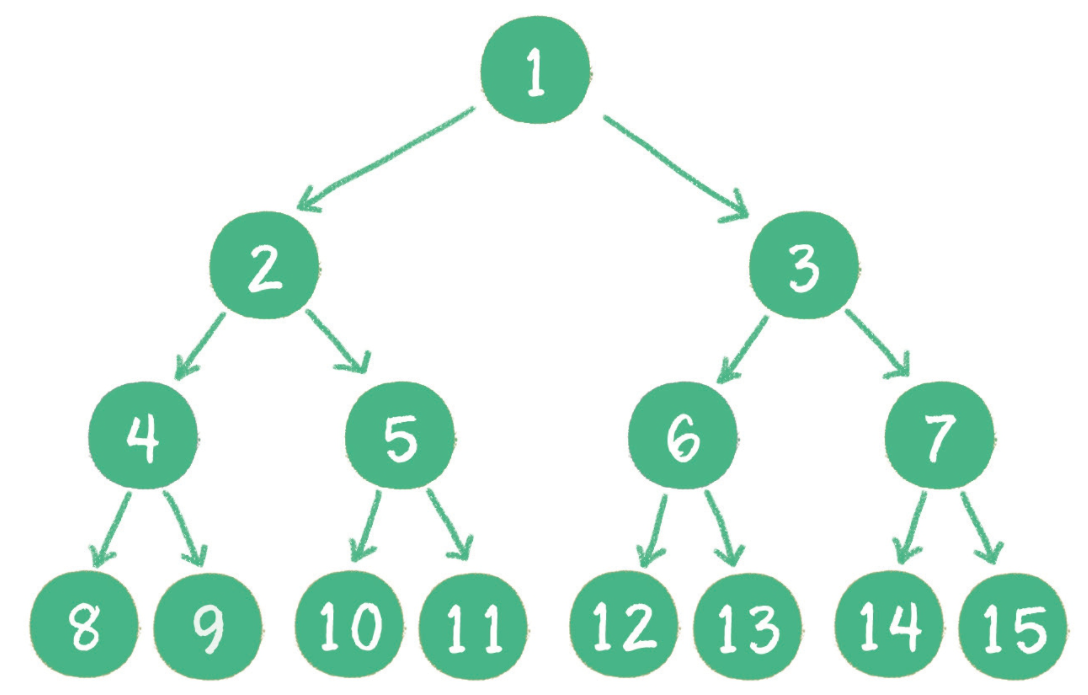

  

• 完全二叉树：满足节点从1-n的树，可以顺序储存

  完全二叉树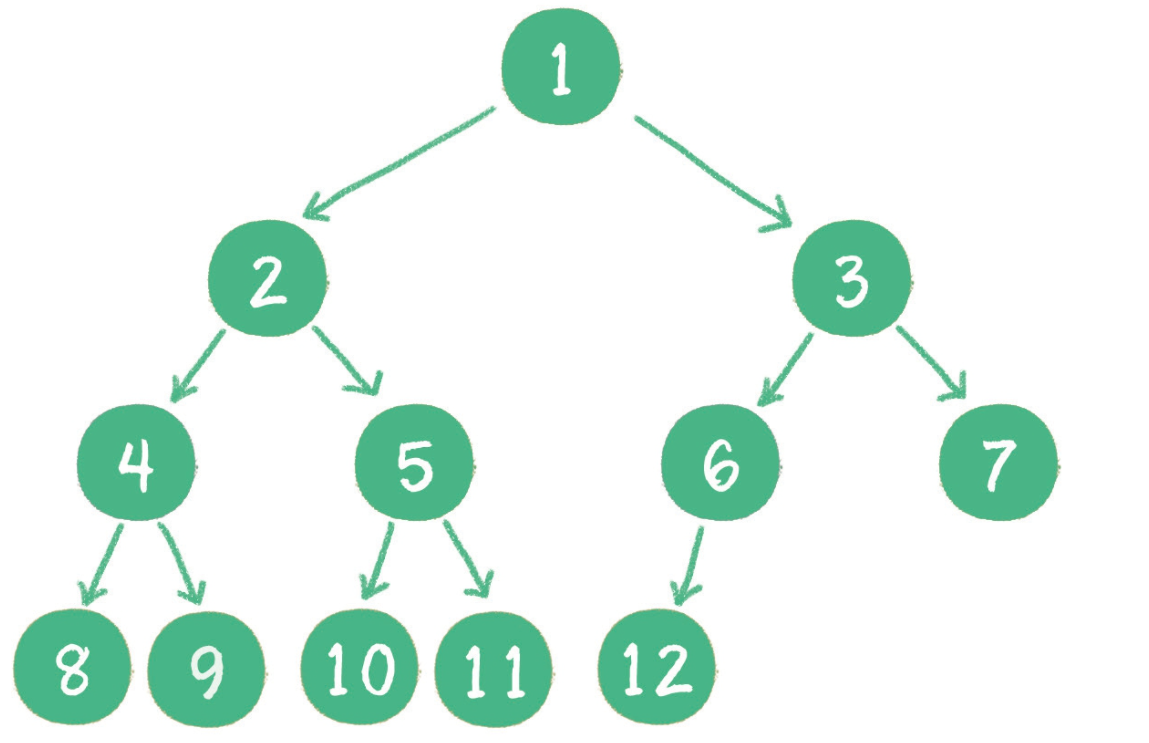

  

• 二叉查找树（Binary Search Tree）：也叫二叉搜索树、二叉排序树。若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值； 它的左、右子树也分别为二叉排序树。

• BST和二叉堆的区别就是，BST是用来查找的，二叉堆是用来排序的。

• 平衡数：一般的二叉查找树的查询复杂度取决于目标结点到树根的距离（即深度），因此当结点的深度普遍较大时，查询的均摊复杂度会上升。为了实现更高效的查询，产生了平衡树。在这里，平衡指所有叶子的深度趋于平衡，更广义的是指在树上所有可能查找的均摊复杂度偏低。

  • AVL树
  • 红黑树

例题

• 默认的框架

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

  struct TreeNode { int val; TreeNode *left; TreeNode *right; TreeNode() : val(0), left(nullptr), right(nullptr) {} TreeNode(int x) : val(x), left(NULL), right(NULL) {} }; //动态创建 TreeNode * dp=new TreeNode(value); //解题框架 if{ 终止条件 } //递归左子树/右子树 //返回值/或者节点操作

• 104 二叉树的最大深度——深度优先搜素

• 给定一个二叉树，找出其最大深度。

  二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

  说明: 叶子节点是指没有子节点的节点。

  学会递归，约束递归结束条件，自底向上，后序遍历

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33

  /** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: int maxDepth(TreeNode* root) { if(root==nullptr){ return 0; } return max(maxDepth(root->left),maxDepth(root->right))+1; } }; class Solution { public: int maxDepth(TreeNode* root) { if(!root){ return 0; } int l=maxDepth(root->left); int r=maxDepth(root->right); return max(l,r)+1; } };

• 919. 完全二叉树插入器

  完全二叉树 是每一层（除最后一层外）都是完全填充（即，节点数达到最大）的，并且所有的节点都尽可能地集中在左侧。

  设计一种算法，将一个新节点插入到一个完整的二叉树中，并在插入后保持其完整。

  实现 CBTInserter 类:

  • CBTInserter(TreeNode root) 使用头节点为 root 的给定树初始化该数据结构；
  • CBTInserter.insert(int v) 向树中插入一个值为 Node.val == val的新节点 TreeNode。使树保持完全二叉树的状态，并返回插入节点 TreeNode 的父节点的值；
  • CBTInserter.get_root() 将返回树的头节点。

• 思路1：使用队列，把能够添加子节点的插入队列，左右节点都添加完后排出队列。

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40

  class CBTInserter { public: TreeNode *m_root; queue<TreeNode*> m_qe; CBTInserter(TreeNode* root) { m_root = root; queue<TreeNode*> qe; qe.push(root); while(qe.size()){ TreeNode* tmp = qe.front(); qe.pop(); if(tmp->left){ qe.push(tmp->left); } if(tmp->right){ qe.push(tmp->right); } if(!tmp->left || !tmp->right){ m_qe.push(tmp); } } } int insert(int val) { TreeNode* new1 = new TreeNode(val); TreeNode* tmp = m_qe.front(); if(!tmp->left){ tmp->left = new1; }else{ tmp->right = new1; m_qe.pop(); } m_qe.push(new1); return tmp->val; } TreeNode* get_root() { return m_root; } };

• 思路2：位操作。注意，若给完全二叉树排序，从1开始，那么最后一个叶子节点假设为x，则其左子树就是2*x；右子树就是2*x+1。因此我们用二进制的位表示左右子树。例如，8号在第三层第一个节点，8的二进制是1000。那么忽略最高位的1，开始，0表示为当前节点的右子树，1表示当前节点的左子树，知道最后的0得到当前节点的位置。

• 

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48

  class CBTInserter { public: queue<TreeNode*> m_qe; TreeNode * m_root; int cnt = 0; CBTInserter(TreeNode* root) { m_root = root; queue<TreeNode*> qe; qe.push(root); while(qe.size()){ TreeNode* tmp = qe.front(); qe.pop(); ++cnt; if(tmp->left){ qe.push(tmp->left); } if(tmp->right){ qe.push(tmp->right); } } } int insert(int val) { TreeNode* newR = new TreeNode(val); TreeNode * curr = m_root; ++cnt;//当前节点的位置 int hight = 32 - __builtin_clz(cnt); hight = hight-1;//忽略最高位的1 //定位父节点 for(int i = hight-1;i>=1;--i){ if(cnt&(1<<i)){ curr = curr->right; }else{ curr = curr->left; } } if(cnt&1){ curr->right = newR; }else{ curr->left = newR; } return curr->val; } TreeNode* get_root() { return m_root; } };

• 110 判断是否为平衡二叉树

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60

  /** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: //自顶向下，类似前序遍历 int height(TreeNode * root){ if(root==nullptr){ return 0; } return max(height(root->left),height(root->right))+1; } bool isBalanced(TreeNode* root) { if(root==nullptr){ return true; } //前序遍历，先根，后左，后右 return (abs(height(root->left)-height(root->right))<=1)&&(isBalanced(root->left))&& (isBalanced(root->right)); } }; class Solution { public: //自底向上，类似后序遍历 int height(TreeNode * root){ if(root==nullptr){ return 0; } int left=height(root->left);//后序遍历 int right=height(root->right); if(left==-1||right==-1||(abs(left-right)>1)){ return -1; }else{ return max(left,right)+1; } } bool isBalanced(TreeNode* root) { int result=height(root); if(result==-1){ return false; } return true; } };

• 543. 二叉树的直径

  给定一棵二叉树，你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32

  /** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: //深度优先搜索 int ans; int dep_tree(TreeNode *root){ if(root==nullptr){ return 0; } int left=dep_tree(root->left); int right=dep_tree(root->right); ans=max(left+right,ans); return max(left,right)+1; } int diameterOfBinaryTree(TreeNode* root) { ans=0; dep_tree(root); return ans; } };

• 437. 路径总和 III

  给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的 路径 的数目。

  路径 不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40

  /** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: //双重深度优先搜索,两次前序遍历，以该根节点 int check_root(TreeNode *root,int targetSum){ if(root==nullptr){ return 0; } int ans=0; if(root->val==targetSum){ ++ans; } ans+=check_root(root->left, targetSum-root->val); ans+=check_root(root->right, targetSum-root->val); return ans; } //查找整棵树 int pathSum(TreeNode* root, int targetSum) { if(root==nullptr){ return 0; } int ret=0; ret+=check_root(root, targetSum); ret+=pathSum(root->left, targetSum);//以左子树为新的节点判断路径 ret+=pathSum(root->right,targetSum); return ret; } };

前缀和

• 一种预处理手段

• 二、如何得到前缀和？

  一维前缀和：

  很容易就可以发现：

  代码实现如下：

  1 2 3 4 5

  for(int i=0;i<n;i++) { if(i==0) y[i]=x[i]; else y[i]=y[i-1]+x[i]; }

  二维前缀和：（面积）

  二维前缀和实际上就是一个矩阵内值的和，而矩阵又可以由两个行数或列数少一的子矩阵组合后，删去重合部分再加上右下角的值来构成，也就是以下式子：

  

  代码实现如下：

• 101 镜像对称二叉树

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34

  /** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: //辅助 bool check_symmertric(TreeNode *left,TreeNode *right){ //&&的情况下尽量return false，只有完全可能才应该返回true if(!left&&!right){ return true; } if(!left||!right){ return false; } if(left->val!=right->val){ return false; } return (check_symmertric(left->left, right->right)&&check_symmertric(left->right,right->left)); } bool isSymmetric(TreeNode* root) { //深度优先搜索 return check_symmertric(root->left, root->right); } };

• 1110. 删点成林

  给出二叉树的根节点 root，树上每个节点都有一个不同的值。

  如果节点值在 to_delete 中出现，我们就把该节点从树上删去，最后得到一个森林（一些不相交的树构成的集合）。

  返回森林中的每棵树。你可以按任意顺序组织答案。

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44

  /** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: //后序遍历，辅助函数 TreeNode * dfs(TreeNode * root, unordered_set<int> &dic,vector<TreeNode *> &forests){ if(!root){ return nullptr; } //后序遍历 root->left=dfs(root->left, dic, forests);//更改节点 root->right=dfs(root->right,dic,forests); if(dic.count(root->val)){ if(root->left){ forests.push_back(root->left); } if(root->right){ forests.push_back(root->right); } root=nullptr;//删除节点 } return root;//返回 } vector<TreeNode*> delNodes(TreeNode* root, vector<int>& to_delete) { unordered_set<int> dic_dor(to_delete.begin(),to_delete.end());//使用哈希查询 vector<TreeNode *> forests; TreeNode * ret=dfs(root, dic_dor,forests);//保存根节点 if(ret){ forests.push_back(ret); } return forests; } };

• 637 二叉树的层平均值

  • 给定一个非空二叉树, 返回一个由每层节点平均值组成的数组。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39

  /** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: //广度优先搜索,使用队列，一个节点队列，两个入队 vector<double> averageOfLevels(TreeNode* root) { vector<double> out; queue<TreeNode *> now; double sum=0; now.push(root); while(!now.empty()){ int num=now.size(); for(int i=0;i<num;++i){ TreeNode* temp=now.front(); now.pop(); sum+=temp->val; if(temp->left){ now.push(temp->left); } if(temp->right){ now.push(temp->right); } } sum=sum/num; out.push_back(sum); sum=0; } return out; } };

• 105 从前序和中序排列构建二叉树

  前提是所有的值没有重复

  • 思路

  • 

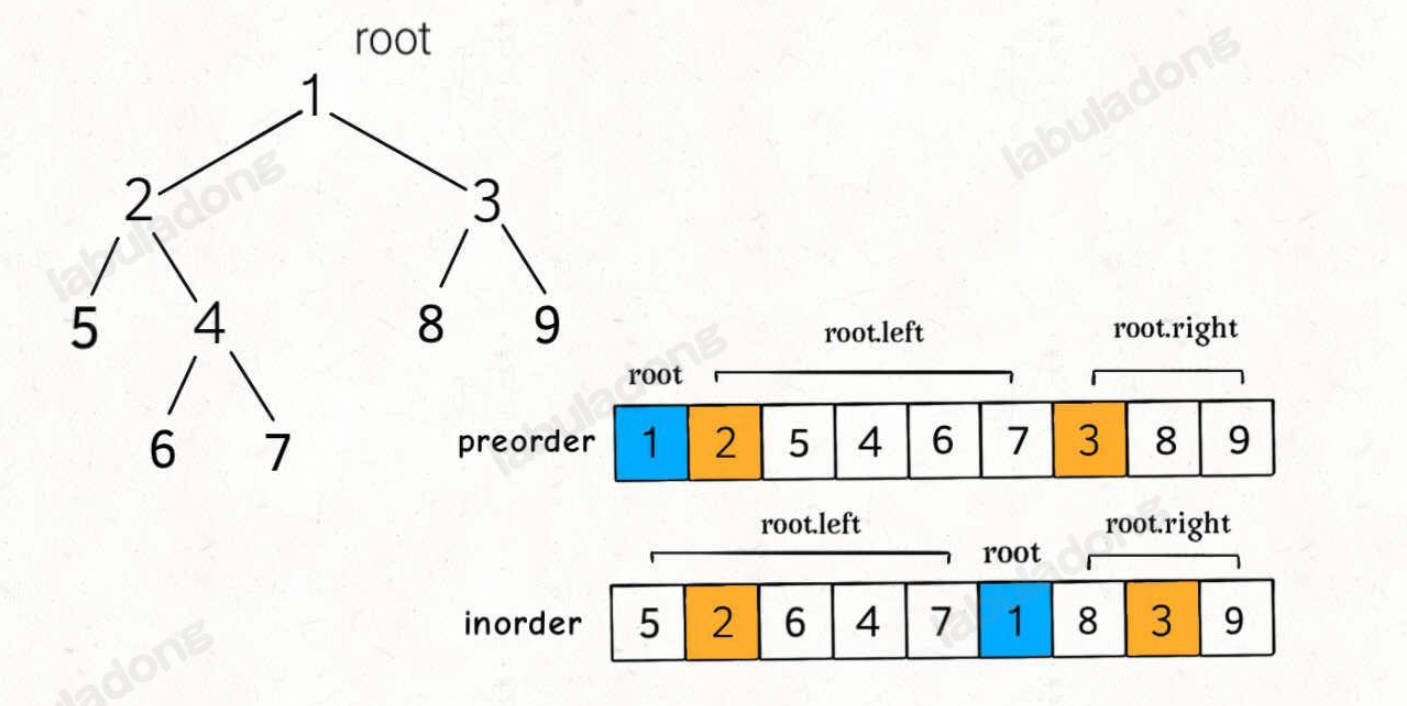
    前序遍历结果第一个就是根节点的值，然后再根据中序遍历结果确定左右子树的节点。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48

  /** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: TreeNode * mybuildtree(vector<int>& preorder, vector<int>& inorder,unordered_map<int, int> &index1, int pre_left, int pre_right,int in_left ,int in_right){ //等于表示是一个数，要包含 if(pre_left>pre_right){ return nullptr; } //找根节点 int root=pre_left; TreeNode * node=new TreeNode(preorder[root]); //找中序结点 int left_index=index1[preorder[root]]; int left_len=left_index-in_left; //递归左子树 node->left=mybuildtree(preorder,inorder, index1, pre_left+1, pre_left+left_len, in_left, left_index-1); //递归右子树 node->right=mybuildtree(preorder, inorder, index1, pre_left+left_len+1, pre_right, left_index+1, in_right); return node; } TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) { if(preorder.empty()) return nullptr; //构建哈希表 unordered_map<int,int> hash1; int n=preorder.size(); for(int i=0;i<n;++i){ hash1[inorder[i]]=i; } TreeNode* out=mybuildtree(preorder, inorder, hash1, 0, n-1, 0, n-1); return out; } };

• 1469. 寻找所有的独生节点

  二叉树中，如果一个节点是其父节点的唯一子节点，则称这样的节点为 “独生节点” 。二叉树的根节点不会是独生节点，因为它没有父节点。

  给定一棵二叉树的根节点 root ，返回树中 所有的独生节点的值所构成的数组 。数组的顺序 不限 。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26

  class Solution { public: //直接前序遍历就是了 vector<int> ret; void bacektracking(TreeNode* root){ if(!root->left&&!root->right){ return; } else if(root->left&&!root->right){ ret.emplace_back(root->left->val); bacektracking(root->left); } else if(root->right&&!root->left){ ret.emplace_back(root->right->val); bacektracking(root->right); }else{ bacektracking(root->left); bacektracking(root->right); } } vector<int> getLonelyNodes(TreeNode* root) { ret.clear(); bacektracking(root); return ret; } };

• 144 二叉树的前序遍历

  • 递归法

    1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31

    /** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: void helper(TreeNode *root,vector<int> &ret){ if(!root){ return; } ret.push_back(root->val); helper(root->left, ret); helper(root->right, ret); return; } vector<int> preorderTraversal(TreeNode* root) { vector<int> ret; if(!root){ return ret; } helper(root, ret); return ret; } };

  • 迭代法，使用栈

    1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37

    /** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: vector<int> preorderTraversal(TreeNode* root) { vector<int> ret; if(!root){ return ret; } //非递归，使用栈,因为lifo，所以右节点先入栈 stack<TreeNode *> temp; temp.push(root); while(!temp.empty()){ TreeNode * node=temp.top(); temp.pop(); ret.push_back(node->val); if(node->right){ temp.push(node->right); } if(node->left){ temp.push(node->left); } } return ret; } };

• 二叉树的中序遍历

  • 递归法

    1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28

    /** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: void helper(TreeNode * root, vector<int> &ret){ if(!root){ return; } helper(root->left, ret); ret.push_back(root->val); helper(root->right, ret); } vector<int> inorderTraversal(TreeNode* root) { vector<int> out; helper(root, out); return out; } };

  • 迭代法

    1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38

    /** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: vector<int> inorderTraversal(TreeNode* root) { vector<int> out; TreeNode * p=root; stack<TreeNode*> temp; if(!root){ return out; } while(p||!temp.empty()){ //疯狂压左子树入栈 while(p){ temp.push(p); p=p->left; } //栈非空 if(!temp.empty()){ TreeNode * temp2=temp.top(); temp.pop(); out.push_back(temp2->val); p=temp2->right; } } return out; } };

• 145 二叉树的后序遍历

  • 递归法

    1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

    class Solution { public: void helper(TreeNode * root, vector<int> & ret){ if(!root){ return; } helper(root->left, ret); helper(root->right, ret); ret.push_back(root->val); } vector<int> postorderTraversal(TreeNode* root) { vector<int> out; helper(root, out); return out; } };

  • 迭代法——镜像类前序遍历

    1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

    class Solution { public: vector<int> postorderTraversal(TreeNode* root) { vector<int> ret; stack<TreeNode *> node; if(!root){ return ret; } node.push(root); while(!node.empty()){ TreeNode * temp=node.top(); node.pop(); ret.push_back(temp->val); //不过先压左节点 if(temp->left){ node.push(temp->left); } if(temp->right){ node.push(temp->right); } } reverse(ret.begin(), ret.end());//反转一下 return ret; } };

  • 迭代法——标志法

    1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32

    class Solution { public: vector<int> postorderTraversal(TreeNode* root) { vector<int> ret; stack<TreeNode *> node; if(!root){ return ret; } TreeNode * temp_root=root; TreeNode * prev=nullptr; while(temp_root || !node.empty()){ //疯狂压左子树 while(temp_root){ node.push(temp_root); temp_root=temp_root->left; } if(!node.empty()){ TreeNode * temp=node.top(); if(!temp->right||temp->right==prev){ ret.push_back(temp->val); node.pop(); prev=temp;//更改标志，已读 temp_root=nullptr;//继续循环 }else{ temp_root=temp->right; } } } return ret; } };

• 二叉树的层序遍历

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28

  class Solution { public: vector<vector<int>> levelOrder(TreeNode* root) { queue<TreeNode*> ret; vector<vector<int>> out; if(!root){ return out; } ret.push(root); while(!ret.empty()){ int n=ret.size(); vector<int> inclu; for(int i=0;i<n;++i){ TreeNode * temp=ret.front(); ret.pop(); inclu.push_back(temp->val); if(temp->left){ ret.push(temp->left); } if(temp->right){ ret.push(temp->right); } } out.push_back(inclu); } return out; } };

• 112. 路径总和

• 给你二叉树的根节点 root 和一个表示目标和的整数 targetSum ，判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。

  叶子节点 是指没有子节点的节点。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

  /** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: bool hasPathSum(TreeNode* root, int targetSum) { if(!root){return false;} //判断是否为叶子节点 if(!root->left&&!root->right){ return root->val==targetSum; } return hasPathSum(root->left,targetSum-root->val)|| hasPathSum(root->right,targetSum-root->val); } };

• 106 从中序遍历和后序遍历创建二叉树

• 思路：后序遍历结果最后一个就是根节点的值，然后再根据中序遍历结果确定左右子树的节点。

  

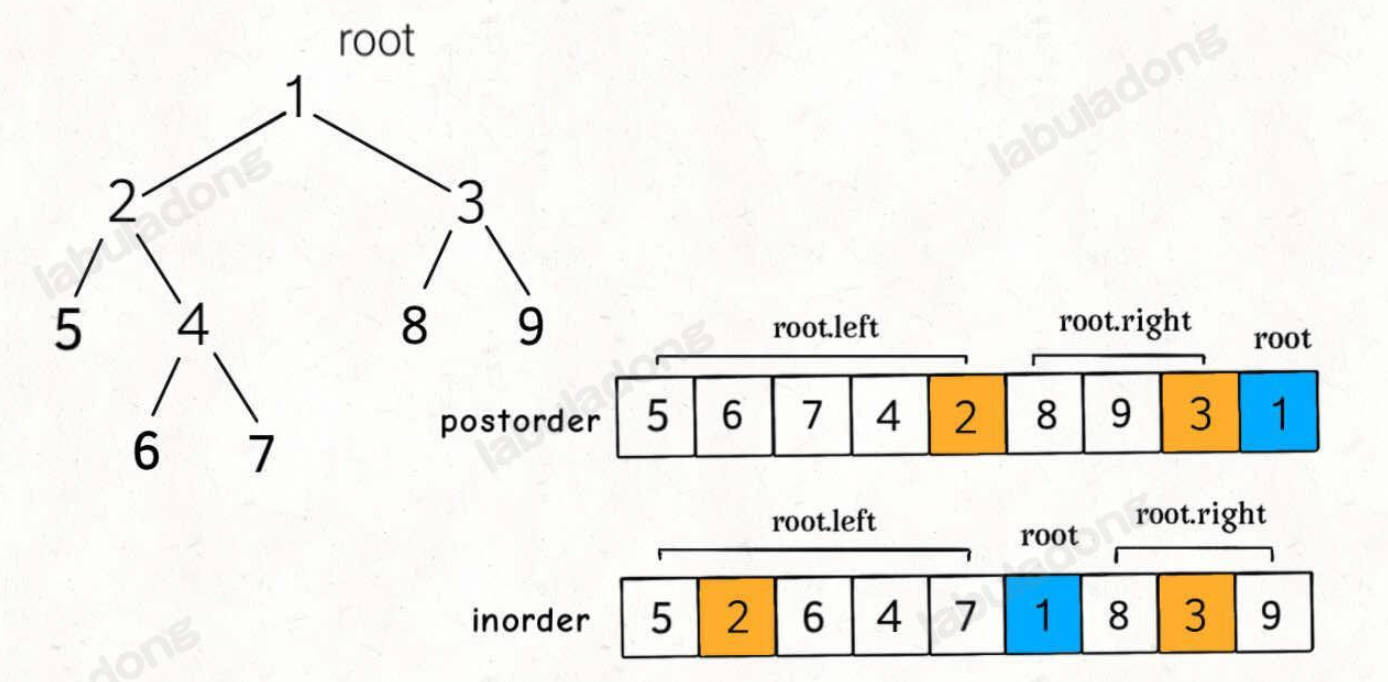
  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

  class Solution { public: TreeNode * mybuild(vector<int>& inorder, vector<int>& postorder,unordered_map<int,int> &index1, int in_begin, int in_end ,int post_begin, int post_end){ if(post_begin>post_end){ return nullptr; } //找根节点 int root=post_end; TreeNode * temp=new TreeNode(postorder[root]);//创建根节点 //找分界线 int mid_indx=index1[postorder[root]]; int len=mid_indx-in_begin; temp->left=mybuild(inorder, postorder, index1, in_begin, mid_indx-1, post_begin, post_begin+len-1); temp->right=mybuild(inorder, postorder, index1, mid_indx+1, in_end, post_begin+len, post_end-1); return temp; } TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) { int n=inorder.size(); //创建哈希表 unordered_map<int,int> index1; for(int i=0;i<n;++i){ index1[inorder[i]]=i; } TreeNode * out= mybuild(inorder,postorder, index1, 0, n-1, 0, n-1); return out; } };

• 116 填充每一个节点的右侧指针next

  • 给定一个 完美二叉树 ，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：

    struct Node { int val; Node *left; Node *right; Node *next; } 填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

    初始状态下，所有 next 指针都被设置为 NULL

  • 层序遍历

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46

  /* // Definition for a Node. class Node { public: int val; Node* left; Node* right; Node* next; Node() : val(0), left(NULL), right(NULL), next(NULL) {} Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {} Node(int _val, Node* _left, Node* _right, Node* _next) : val(_val), left(_left), right(_right), next(_next) {} }; */ class Solution { public: Node* connect(Node* root) { queue<Node *> temp; if(!root){ return nullptr; } temp.push(root); while(!temp.empty()){ int n=temp.size(); for(int i=0;i<n;++i){ Node * ret=temp.front(); temp.pop(); if(i<n-1){ Node * ret1=temp.front(); ret->next=ret1; } if(ret->left){ temp.push(ret->left); } if(ret->right){ temp.push(ret->right); } } } return root; } };

LCA 最近公共祖先

• 236 二叉树的最近公共祖先——LCA

  • 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

    百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

  • 这是已经构建了一棵二叉树。

  • 后序遍历

  • 最重要是会设置条件

  • 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32

    /** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode(int x) : val(x), left(NULL), right(NULL) {} * }; */ class Solution { public: TreeNode * ans; bool dfs(TreeNode* root, TreeNode* p, TreeNode* q){ if(!root){ return false; } bool lef=dfs(root->left, p, q);//左节点是否存在 bool rig=dfs(root->right,p,q); //左右同时包含 或者 其中一个是根节点，另外一个包含,这样保证是最大深度 if((lef&&rig) || ((lef||rig)&&(root->val==p->val||root->val==q->val))){ ans=root; } return lef||rig||root->val==p->val||root->val==q->val; } TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) { dfs(root, p, q); return ans; } };

• 只有后序遍历才能保证是最近的公共祖先

• 669 修剪二叉搜索树

  • 给你二叉搜索树的根节点 root ，同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树，使得所有节点的值在[low, high]中。修剪树不应该改变保留在树中的元素的相对结构（即，如果没有被移除，原有的父代子代关系都应当保留）。 可以证明，存在唯一的答案。

    所以结果应当返回修剪好的二叉搜索树的新的根节点。注意，根节点可能会根据给定的边界发生改变。

  • 思路：小于，剪去左边

    大于，剪去右边

    ​ 在中间，递归左右子树

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31

  /** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: TreeNode* trimBST(TreeNode* root, int low, int high) { //直接先序遍历，根节点的小于low，裁掉左边，返回右边，大于high，裁掉右边，返回左边 if(!root){ return nullptr; } if(root->val<low){ return trimBST(root->right, low, high); } if(root->val>high){ return trimBST(root->left, low, high); } //以上都不发生，遍历左右节点，修剪左右子树。只有这三种情况 root->left=trimBST(root->left, low, high); root->right=trimBST(root->right, low, high); return root; } };

• 思路2：迭代法

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

  class Solution { public: TreeNode* trimBST(TreeNode* root, int low, int high) { //先确定根节点 while(root&&(root->val<low || root->val>high)){ if(root->val<low){ root = root->right; }else{ root = root->left; } } if(root == nullptr){ return nullptr; } //迭代替换左右节点，注意有else，保证最后可以有nullptr for(TreeNode* node = root;node->left;){ if(node->left->val<low){ node->left = node->left->right; }else node = node->left; } for(auto node = root;node->right;){ if(node->right->val>high){ node->right = node->right->left; }else node = node->right; } return root; } };

• 96. 不同的二叉搜索树，

• 求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32

  //思路 ：回溯+备忘录dp class Solution { public: int backtracking(int start, int end, vector<vector<int>> &dp){ //返回条件 if(start>end){ return 1; } //查看dp if(dp[start][end]!=0){ return dp[start][end]; } //递归回溯 int res=0; for(int i=start;i<=end;++i){ int left=backtracking(start, i-1, dp); int right=backtracking(i+1, end, dp); res=res+left*right;//注意是左右子树相乘，实际的根节点就是两个for循环 } dp[start][end]=res; return res; } int numTrees(int n) { vector<vector<int>> dp(n+1,vector<int>(n+1,0)); if(n==1){ return 1; } return backtracking(1, n, dp); } };

• 思路二：能用dp备忘录的一般都可以进行动态规划

  

  

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

  //因为都是顺序的，关键点是G（n）和序列的内容无关，只和序列的长度有关 class Solution { public: int numTrees(int n) { vector<int> G(n + 1, 0); G[0] = 1; G[1] = 1; for (int i = 2; i <= n; ++i) { for (int j = 1; j <= i; ++j) { G[i] += G[j - 1] * G[i - j]; } } return G[n]; } };

• 95 不同的二叉搜索树2

• 给你一个整数 n ，请你生成并返回所有由 n 个节点组成且节点值从 1 到 n 互不相同的不同 二叉搜索树 。可以按 任意顺序 返回答案。

  • 思路，回溯法，后序遍历，分成左右子树进行生成，生成树一般采用后序遍历

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50

  /** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: vector<TreeNode*> backtracking(int begin, int end){ if(begin>end){ return {nullptr}; } vector<TreeNode*> alltree; ///后序遍历,递归回溯 //横向遍历 for(int i=begin;i<=end;++i){ //得到所有左子树集合 vector<TreeNode*> lefttree=backtracking(begin, i-1);//纵向遍历 //得到所有右子树集合 vector<TreeNode*> righttree=backtracking(i+1, end); //接到根节点上 for(auto &l1:lefttree){ for(auto &r1:righttree){ TreeNode * root=new TreeNode(i);//注意一定for里面初始化root,往上传root，才能生成树 root->left=l1; root->right=r1; alltree.push_back(root); } } } return alltree; } vector<TreeNode*> generateTrees(int n) { if(n==0){ return {nullptr}; } return backtracking(1, n); } };

• 863. 二叉树中所有距离为 K 的结点

  给定一个二叉树（具有根结点 root）， 一个目标结点 target ，和一个整数值 k 。

  返回到目标结点 target 距离为 k 的所有结点的值的列表。 答案可以以 任何顺序 返回。

  • 思路：哈希表加深度优先搜索

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57

  /** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode(int x) : val(x), left(NULL), right(NULL) {} * }; */ class Solution { public: vector<int> ret; unordered_map<int,TreeNode *> parents; void findAns(TreeNode* node, TreeNode* from, int depth, int k) { if (node == nullptr) { return; } if (depth == k) { ret.push_back(node->val); return; } //用from节点判断从那来，从而避免重复递归 if (node->left != from) { findAns(node->left, node, depth + 1, k); } if (node->right != from) { findAns(node->right, node, depth + 1, k); } if (parents[node->val] != from) { findAns(parents[node->val], node, depth + 1, k); } } //建立父节点 void findParents(TreeNode* root){ if(!root){ return; } if(root->left){ parents[root->left->val]=root; findParents(root->left); } if(root->right){ parents[root->right->val]=root; findParents(root->right); } } vector<int> distanceK(TreeNode* root, TreeNode* target, int k) { parents.clear(); ret.clear(); findParents(root); findAns(target, nullptr, 0, k); return ret; } };

序列化二叉树

• 剑指 Offer 37. 序列化二叉树

请实现两个函数，分别用来序列化和反序列化二叉树。

你需要设计一个算法来实现二叉树的序列化与反序列化。这里不限定你的序列 / 反序列化算法执行逻辑，你只需要保证一个二叉树可以被序列化为一个字符串并且将这个字符串反序列化为原始的树结构。

**提示：**输入输出格式与 LeetCode 目前使用的方式一致，详情请参阅 LeetCode 序列化二叉树的格式。你并非必须采取这种方式，你也可以采用其他的方法解决这个问题。

• 思路1：采用先序遍历，解码同理采用先序遍历

• 编码格式为val, val, None, None,

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52

  /** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode(int x) : val(x), left(NULL), right(NULL) {} * }; */ class Codec { public: // Encodes a tree to a single string. string serialize(TreeNode* root) { string ret; if(!root){ return "None,"; } ret += to_string(root->val); ret += ","; ret += serialize(root->left); ret += serialize(root->right); return ret; } //没有递归退出条件，因为如果编码正确的是，随着双头队列的元素的删减最终是会自然退出的 TreeNode* dfs(deque<string> &src){ if(src.front()=="None"){ src.pop_front(); return nullptr; } string curr = src.front(); src.pop_front(); TreeNode *ret = new TreeNode(atoi(curr.c_str())); ret->left = dfs(src); ret->right = dfs(src); return ret; } // Decodes your encoded data to tree. TreeNode* deserialize(string data) { //先解码 deque<string> curr; stringstream ss(data); string s2(""); while(getline(ss, s2, ',')) { curr.emplace_back(s2); } return dfs(curr); } };

• 思路2：采用层序遍历。

基环树

• 基环树是一种图，它由一个环组成，环上每个点都是一棵树点树根，所以称为基环树。

基环内向树

• 首先它是一个有向图，它构成类似基环树的结构，有一个特点是每个点都有且只有一个出度，并且环外的节点方向指向环内。
• 

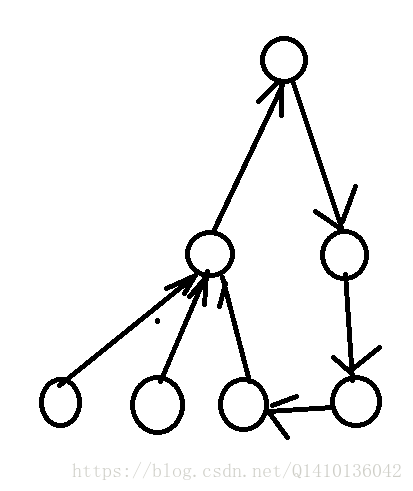
基环外向树

• 与基环内向树相反，它有且只有一个入度（基环内向树是出度），并且并且由环指向环外。
• 

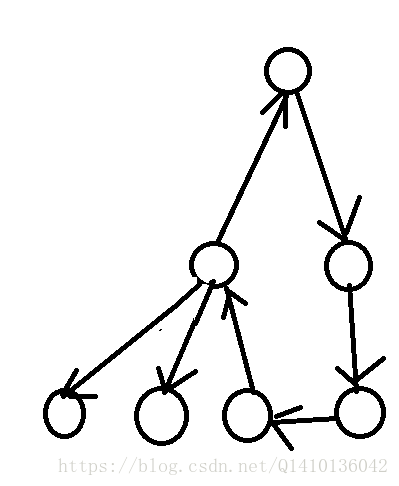
通用处理方法

这种方法针对的是基环内向树。

我们可以通过一次拓扑排序「剪掉」所有树枝，因为拓扑排序后，树枝节点的入度均为 0，基环节点的入度均为 1。这样就可以将基环和树枝分开，从而简化后续处理流程：

• 如果要遍历基环，可以从拓扑排序后入度为 1 的节点出发，在图上搜索；
• 如果要遍历树枝，可以以基环与树枝的连接处为起点，顺着反图来搜索树枝（搜索入度为 00 的节点），从而将问题转化成一个树形问题。

例题

• 6134. 找到离给定两个节点最近的节点

  给你一个 n 个节点的 有向图 ，节点编号为 0 到 n - 1 ，每个节点 至多 有一条出边。

  有向图用大小为 n 下标从 0 开始的数组 edges 表示，表示节点 i 有一条有向边指向 edges[i] 。如果节点 i 没有出边，那么 edges[i] == -1 。

  同时给你两个节点 node1 和 node2 。

  请你返回一个从 node1 和 node2 都能到达节点的编号，使节点 node1 和节点 node2 到这个节点的距离 较大值最小化。如果有多个答案，请返回 最小 的节点编号。如果答案不存在，返回 -1 。

  注意 edges 可能包含环。

• 思路：遍历两个节点求出所有的连接节点，最后判断最短距离就好。

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73

  //我写的 class Solution { public: int closestMeetingNode(vector<int>& edges, int node1, int node2) { unordered_map<int,int> distNod1; distNod1[node1] = 0; int step = 0; while(1){ int next = edges[node1]; if(next==-1){ break; } if(distNod1.count(next)){ break; } ++step; distNod1[next] = step; node1 = next; } unordered_map<int,int> distNod2; set<pair<int,int>> ret; distNod2[node2] = 0; if(distNod1.count(node2)){ ret.insert(pair<int,int>{distNod1[node2],node2}); } step = 0; while(1){ int next = edges[node2]; if(next==-1){ break; } if(distNod2.count(next)){ break; } ++step; distNod2[next] = step; if(distNod1.count(next)){ ret.insert(pair<int,int>{max(distNod1[next],step),next}); } node2 = next; } if(ret.size()){ return (*ret.begin()).second; } return -1; } }; //大神写的 class Solution { public: int closestMeetingNode(vector<int> &edges, int node1, int node2) { //时间复杂度O（n） int n = edges.size(), min_dis = n, ans = -1; auto calc_dis = [&](int x) -> vector<int> { vector<int> dis(n, n); //x>0判断终点，dis[x]==n判环 for (int d = 0; x >= 0 && dis[x] == n; x = edges[x]) dis[x] = d++; return dis; }; auto d1 = calc_dis(node1), d2 = calc_dis(node2); //计算较大值最小的节点 for (int i = 0; i < n; ++i) { int d = max(d1[i], d2[i]); if (d < min_dis) { min_dis = d; ans = i; } } return ans; } };

• 6135. 图中的最长环

  给你一个 n 个节点的 有向图 ，节点编号为 0 到 n - 1 ，其中每个节点 至多 有一条出边。

  图用一个大小为 n 下标从 0 开始的数组 edges 表示，节点 i 到节点 edges[i] 之间有一条有向边。如果节点 i 没有出边，那么 edges[i] == -1 。

  请你返回图中的 最长 环，如果没有任何环，请返回 -1 。

  一个环指的是起点和终点是 同一个 节点的路径。

• 思路：不用floyd判环，超时。直接加入一个时间戳判断，同时也可判断是否访问当前节点。复杂度O(N)

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

  //大神的思路 class Solution { public: //使用时间戳 int longestCycle(vector<int> &edges) { int n = edges.size(), ans = -1; vector<int> time(n,0); for (int i = 0, clock = 1; i < n; ++i) { if (time[i]) continue; //x>0判断非末尾节点 for (int x = i, start_time = clock; x >= 0; x = edges[x]) { if (time[x]) { // 重复访问 //大于等于这次循环的开始时间，才能说明是这个环的，否则存在多个环交叉判断失败 if (time[x] >= start_time) ans = max(ans, clock - time[x]); //找到第一个就退出了，否则超时 break; } time[x] = clock++; } } return ans; } };

• 我写的，存在很多冗余的信息

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34

  class Solution { public: int longestCycle(vector<int>& edges) { int len = edges.size(); vector<bool> visites(len,false); int ans = -1; for(int i = 0;i<len;++i){ if(visites[i]){ continue; } int clock = 1; visites[i] = true; if(edges[i]==-1){ continue; } unordered_map<int,int> times; times[i] = clock; int curr = edges[i]; while(curr!=-1&&!times.count(curr)){ if(visites[curr]){ curr = -1; break; } visites[curr] = true; times[curr] = ++clock; curr = edges[curr]; } if(curr!=-1){ ans = max(ans,clock+1-times[curr]); } } return ans; } };

位运算

基本理论

• C++ 提供了按位与（&）、按位或（| ）、按位异或（^）、取反（~）、左移（<<）、右移（>>）这 6 种位运算符。 这些运算符只能用于整型操作数，即只能用于带符号或无符号的 char、short、int 与 long 类型。

• 

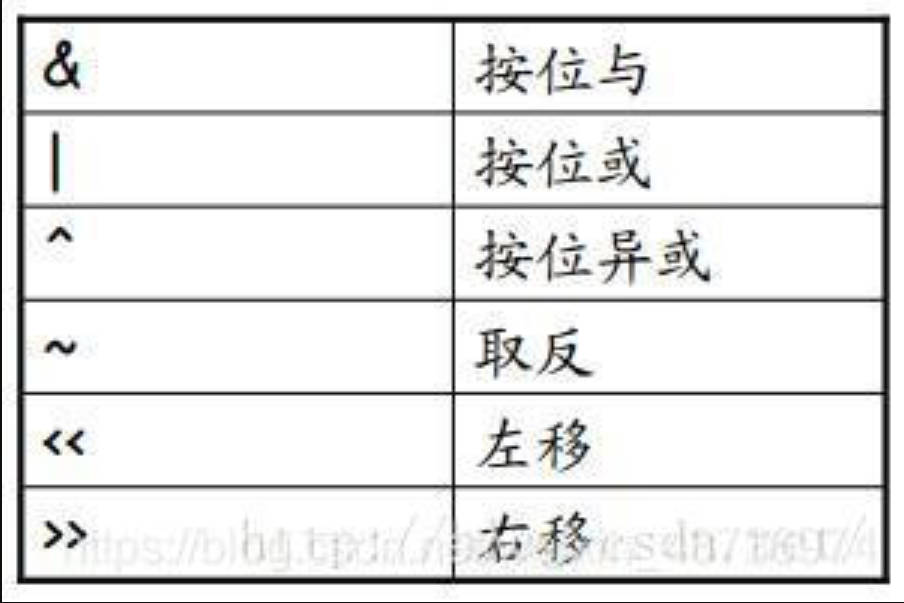
• 左移：依次向左移，低位补0；表现为乘2。负数会保留最高的符号位。

• 右移：依次向右移，高位补0；表现除以2。负数会保留最高的符号位。

• Brian Kernighan 算法

  该算法可以被描述为这样一个结论：记 f(x) 表示 x 和 x-1 进行与运算所得的结果（即 f(x)=x & (x−1)），那么f(x) 恰为 x 删去其二进制表示中最右侧的 1 的结果。

• 201. 数字范围按位与

  给你两个整数 left 和 right ，表示区间 [left, right] ，返回此区间内所有数字 按位与 的结果（包含 left 、right 端点）。

  • 思路：找出公共前缀和，后面补0
  • 

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

  class Solution { public: int rangeBitwiseAnd(int left, int right) { int m=left; int n=right; int shift=0; while(m<n){ m>>=1;//右移等于，复合运算符 n>>=1; ++shift; } return m<<shift; } };

  • 方法2：采用Brian Kernighan 算法，一直删去n后面的1，知道n<=m

  1 2 3 4 5 6 7 8 9 10 11 12

  class Solution { public: int rangeBitwiseAnd(int left, int right) { int m=left; int n=right; while(n>m){ n&=(n-1); } return n; } };

• 题目：请编写一个函数用于判断输入的int数是否是-2的整数次幂加1，即$ ((-2)^N+1)$

• 思路：先对n-1取绝对值，然后判断n&(n-1)==0，因为2的整数次幂，其二进制表示只有一个1。n-1和n按位与，一定等于0。

• 1 2 3 4 5 6 7 8 9 10 11 12 13

  #include <bits/stdc++.h> using namespace std; bool isPlusMod(int n){ int temp = n-1; temp = abs(temp); return ((temp&(temp-1))==0); } int main() { bool coss = isPlusMod(5); return 0; }

• 题目：请实现一个函数，输入一个整数，输出该数二进制表示中1的个数。

• 思路1：左移统计二进制中1的个数，但是这种解法循环次数等于二进制的位数，32位的整数需要循环32次。

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23

  int NumberOfOne(int n) { int count = 0; unsigned int flag = 1; while (flag > 0) { if (n & flag) { ++count; } flag = flag << 1; } return count; } int main() { int nn = NumberOfOne(-7); return 0; } /*进制 -7 11111001 补码 结果 30 ./

• 思路2：整数中有几个1就循环几次。把一个整数减去1, 再和原整数做与算法，会把整数最右边的1变为0。

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14

  int NumberOfOne(int n) { int count = 0; while (n) { ++count; n=n&(n-1);//去除最后的1 } return count; } int main() { int nn = NumberOfOne(7); return 0; }

格雷码

• 89. 格雷编码

  n 位格雷码序列 是一个由 $2^n$ 个整数组成的序列，其中：

  • 每个整数都在范围 [0, 2n - 1] 内（含 0 和 2n - 1）
  • 第一个整数是 0
  • 一个整数在序列中出现 不超过一次
  • 每对 相邻 整数的二进制表示 恰好一位不同 ，且
  • 第一个 和 最后一个 整数的二进制表示 恰好一位不同

  给你一个整数 n ，返回任一有效的 n 位格雷码序列 。

  • 解法1：按格雷码定义，由原本的二进制数得到格雷码，保留最高位；次高位为二进制码最高位和次高位相异或，其余位数格雷码依次类推。

  • 1 2 3 4 5 6 7 8 9 10 11 12

    class Solution { public: vector<int> grayCode(int n) { vector<int> ret(1<<n);//赋予数组大小 iota(ret.begin(), ret.end(), 0); for(int i=0;i<ret.size();++i){ int temp=ret[i]>>1;//保留最高位 ret[i]=ret[i]^temp;//依次异或 } return ret; } };

  • 解法2：镜像生成

  • 

  • 步骤1：1位格雷码有两个码字——0和1；

  • 步骤2：(n+1)位格雷码中的前$2^n$个码字等于n位格雷码的码字，按顺序书写，加前缀0；

  • 步骤3：(n+1)位格雷码中的后$2^n$个码字等于n位格雷码的码字，按逆序书写，加前缀1;

  • 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

    class Solution { public: vector<int> grayCode(int n) { vector<int> ret; ret.push_back(0);//先加0 int first=1;//前缀 for (int i = 1; i <= n; i++) { int m = ret.size(); //翻转+前缀 for (int j = m - 1; j >= 0; j--) { ret.push_back(ret[j]+first); } //前缀更替 first=first<<1; } return ret; } };

正则表达式

基本理论

• 掌握特殊字符、限定符、定位符

• 特殊字符：有些符号在正则表达式中有特殊含义，比如星号 *，要匹配时必须先用反斜杠 \ 转义，\* 表示星号字符。

• 特殊字符	转义表达	特殊含义
  ()	\(\)	标记一个子表达式的开始和结束位置。子表达式可以获取供以后使用
  $	\$	匹配输入字符串的结尾位置
  *	\*	匹配前面的子表达式零次或多次
  +	\+	匹配前面的子表达式一次或多次
  .	\.	匹配除换行符 \n 之外的任何单字符
  [ ]	\[\]	标记一个中括号表达式的开始。要匹配 [，请使用 [。
  ?	\?	匹配前面的子表达式零次或一次，或指明一个非贪婪限定符
  \	\\	将下一个字符标记为或特殊字符、或原义字符、或向后引用、或八进制转义符
  ^	\^	匹配输入字符串的开始位置，除非在方括号表达式中使用，当该符号在方括号表达式中使用时，表示不接受该方括号表达式中的字符集合
  {}	\{\}	标记限定符表达式的开始
  |	\|	指明两项之间的一个选择

• 限定符：限定符用来指定正则表达式的一个给定组件必须要出现多少次才能满足匹配。 *、+ 限定符都是贪婪的，因为它们会尽可能多的匹配文字。通过在 *、+ 或 ? 限定符之后放置 ?，该表达式从”贪心”表达式转换为”非贪心”表达式或者最小匹配。

  • 字符	描述
    *	匹配前面的子表达式零次、一次或多次，等价于{0,}。例如，zo* 能匹配 z、zo、zoo 和 zoooooooo。
    +	匹配前面的子表达式一次或多次，等价于 {1,}。例如，zo+ 能匹配 zo、zoo 和 zoooo，但不能匹配 z。
    ?	匹配前面的子表达式零次或一次，等价于 {0,1}。例如，do(es)? 可以匹配 do 中的 do，does 中的 does，doxy 中的 do 。
    {n}	匹配确定的 n 次（非负整数）。例如，o{2} 不能匹配 Bob 中的 o，但是能匹配 food 中的 oo。
    {n,}	至少匹配 n 次（非负整数）。例如，’o{2,}’ 不能匹配 “Bob” 中的 ‘o’，但能匹配 “foooood” 中的所有 o。’o{1,}’ 等价于 ‘o+’。’o{0,}’ 则等价于 ‘o*’。
    {n,m}	最少匹配 n 次且最多匹配 m 次（m 和 n 均为非负整数，且n <= m）。例如，”o{1,3}” 将匹配 “fooooood” 中的前三个 o。注意在逗号和两个数之间不能有空格。

• 定位符：定位符使您能够将正则表达式固定到行首或行尾，或一个单词的开头或结尾。

  定位符用来描述字符串或单词的边界，^ 和 $ 分别指字符串的开始与结束，\b 描述单词的前或后边界，\B 表示非单词边界。 注意：不能将限定符与定位符一起使用。由于在紧靠换行或者字边界的前面或后面不能有一个以上位置，因此不允许诸如 ^* 之类的表达式。

• 定位符	表达含义
  ^	字符串开始的位置
  $	字符串结束的位置
  \b	限定单词(字)的字符，常用来确定一个单词，可以结合两个‘\b’使用
  \B	限定非单词(字)边界的字符，用的很少

• grep 命令从输入文件中查找匹配到给定模式列表的行。发现匹配到的行后，默认情况下会复制这一行到标准输出流，也可以通过选项产生任何其他类型的输出。

  grep 匹配文本时，对输入行长度没有限制（但受内存限制），并且可以匹配一行中的任意字符。如果输入文件的最后一个字节不是换行符，那么 grep 会提供一个。由于换行符也是模式列表的分隔符，因此无法在文本中匹配换行符

• awk 是一种程序设计语言，语言风格类似 C 语言，设计目的是写那种一行搞定事情的脚本，常用于文本处理的脚本。包含常用的内置函数，支持用户函数和动态正则表达式，支持数组。

  awk 是一种弱类型语言，不需要提前声明就可以使用变量，变量的类型转换也是隐含的，在不同的上下文中变量可能是不同类型。awk 的字符串连结操作不需要任何操作符，只要把需要连结的串并列写在一起即可。

• 193. 有效电话号码

  给定一个包含电话号码列表（一行一个电话号码）的文本文件 file.txt，写一个单行 bash 脚本输出所有有效的电话号码。

  你可以假设一个有效的电话号码必须满足以下两种格式： (xxx) xxx-xxxx 或 xxx-xxx-xxxx。（x 表示一个数字）

  你也可以假设每行前后没有多余的空格字符。

• 示例：

  假设 file.txt 内容如下：

  1 2 3

  987-123-4567 123 456 7890 (123) 456-7890

  你的脚本应当输出下列有效的电话号码：

  1 2	987-123-4567 (123) 456-7890

  • 1	grep -P '^([0-9]{3}-|\([0-9]{3}\) )[0-9]{3}-[0-9]{4}$' file.txt

单调栈

• 一次遍历计算右边第一个严格小于和左边第一个小于等于的位置

• 1 2 3 4 5 6 7 8 9

  for(int i = 0;i<n;++i){ while(st.size()&& heights[st.top()]>heights[i]){ right[st.top()] = i; st.pop(); } //左边小于等于没关系 left[i] = (st.empty() ? -1 : st.top()); st.emplace(i); }

• 907. 子数组的最小值之和

  给定一个整数数组 arr，找到 min(b) 的总和，其中 b 的范围为 arr 的每个（连续）子数组。

  由于答案可能很大，因此 返回答案模 10^9 + 7 。

• 2104. 子数组范围和

  给你一个整数数组 nums 。nums 中，子数组的 范围 是子数组中最大元素和最小元素的差值。

  返回 nums 中 所有 子数组范围的 和 。

  子数组是数组中一个连续 非空 的元素序列。

• 思路1：暴力枚举，固定左边界，遍历右边界，更新最大最小值即可，时间复杂度$O(n^2)$ 。

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

  class Solution { public: using ll = long long; long long subArrayRanges(vector<int>& nums) { int n = nums.size(); ll ret = 0L; for(int i = 0;i<n;++i){ int minidx = nums[i]; int maxidx = nums[i]; for(int j = i+1;j<n;++j){ minidx = min(minidx,nums[j]); maxidx = max(maxidx,nums[j]); ret += (maxidx-minidx); } } return ret; } };

• 思路2：单调栈法。

• 需要注意的是一个取等号，一个不取等号，防止重复计算

• 

• 

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55

  class Solution { public: using ll = long long; long long subArrayRanges(vector<int>& nums) { stack<int> st; int n = nums.size(); vector<int> leftmin(n,-1);//左边第一个严格小于 vector<int> rightmin(n,n);//右边第一个小于等于 vector<int> leftmax(n,-1);//左边第一个严格大于 vector<int> rightmax(n,n);//右边第一个大于等于 for(int i = 0;i<n;++i){ while(st.size()&&nums[st.top()]>=nums[i]){ int curr = st.top(); st.pop(); rightmin[curr] = i; } st.emplace(i); } while(st.size()) st.pop(); for(int i = 0;i<n;++i){ while(st.size()&&nums[st.top()]<=nums[i]){ int curr = st.top(); st.pop(); rightmax[curr] = i; } st.emplace(i); } while(st.size()) st.pop(); for(int i = n-1;i>=0;--i){ while(st.size()&&nums[st.top()]>nums[i]){ int curr = st.top(); st.pop(); leftmin[curr] = i; } st.emplace(i); } while(st.size()) st.pop(); for(int i = n-1;i>=0;--i){ while(st.size()&&nums[st.top()]<nums[i]){ int curr = st.top(); st.pop(); leftmax[curr] = i; } st.emplace(i); } ll ret = 0L; for(int i = 0;i<n;++i){ ll tmp1 = ((rightmax[i]-i)*(i-leftmax[i])); ll tmp2 = ((rightmin[i]-i)*(i-leftmin[i])); ret += (tmp1-tmp2)*nums[i]; } return ret; } };

• 1856. 子数组最小乘积的最大值

  一个数组的 最小乘积 定义为这个数组中 最小值 乘以 数组的 和 。

  • 比方说，数组 [3,2,5] （最小值是 2）的最小乘积为 2 * (3+2+5) = 2 * 10 = 20 。

  给你一个正整数数组 nums ，请你返回 nums 任意 非空子数组 的最小乘积 的 最大值 。由于答案可能很大，请你返回答案对 109 + 7 取余 的结果。

  请注意，最小乘积的最大值考虑的是取余操作 之前 的结果。题目保证最小乘积的最大值在 不取余 的情况下可以用 64 位有符号整数 保存。

  子数组 定义为一个数组的 连续 部分。

• 思路：单调战车处理左右第一个严格小于当前元素的元素的位置；同时预处理前缀和，最后遍历一遍判断即可。

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38

  class Solution { public: const int mod = 1000000007; using ll = long long; int maxSumMinProduct(vector<int>& nums) { int n = nums.size(); vector<ll> sumPre(n,0); sumPre[0] = nums[0]; vector<int> left(n,-1); vector<int> right(n,n); for(int i = 1;i<n;++i){ sumPre[i] = sumPre[i-1]+(ll)nums[i]; } stack<int> st; for(int i = 0;i<n;++i){ while(st.size()&&nums[st.top()]>nums[i]){ right[st.top()] = i; st.pop(); } st.emplace(i); } while(st.size()) st.pop(); for(int i = n-1;i>=0;--i){ while(st.size()&&nums[st.top()]>nums[i]){ left[st.top()] = i; st.pop(); } st.emplace(i); } ll ret = 0L; for(int i = 0;i<n;++i){ ll tmp = sumPre[right[i]-1] - sumPre[left[i]+1] + nums[left[i]+1]; tmp = tmp*nums[i];//在这里取模会报错，要保证是最终答案再取模 ret = max(ret,tmp); } return (int)(ret%mod); } };

• 84. 柱状图中最大的矩形

  给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

  求在该柱状图中，能够勾勒出来的矩形的最大面积。

• 思路：计算左右两边第一个严格小于当前元素的元素的位置

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

  class Solution { public: int largestRectangleArea(vector<int>& heights) { int n = heights.size(); //使用单调栈,分别计算左边第一个严格小于和右边第一个严格小于的序列 vector<int> left(n,-1); vector<int> right(n,n); stack<int> st; for(int i = 0;i<n;++i){ while(st.size()&& heights[st.top()]>heights[i]){ right[st.top()] = i; st.pop(); } //左边小于等于没关系 left[i] = (st.empty() ? -1 : st.top()); st.emplace(i); } int ret = 0; for(int i = 0;i<n;++i){ int tmp = heights[i] * (right[i]-left[i]-1); ret = max(ret,tmp); } return ret; } };

• 剑指 Offer II 039. 直方图最大矩形面积

  给定非负整数数组 heights ，数组中的数字用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

  求在该柱状图中，能够勾勒出来的矩形的最大面积。

• 思路：和上面那题没有任何区别，可以分两次遍历；两次遍历可以控制都是严格小于；一次遍历的话可以只能一边严格小于一边小于等于。但是结果没什么区别。

• 一次遍历时间更快

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23

  class Solution { public: int largestRectangleArea(vector<int>& heights) { int n = heights.size(); vector<int> left(n,-1); vector<int> right(n,n); stack<int> st; //一次遍历，右边严格小于，左边小于等于 for(int i = 0;i<n;++i){ while(st.size()&&heights[st.top()]>heights[i]){ right[st.top()] = i; st.pop(); } if(st.size()) left[i] = st.top(); st.emplace(i); } int ret = 0; for(int i = 0;i<n;++i){ ret = max(ret,heights[i]*(right[i]-left[i]-1)); } return ret; } };

• 901. 股票价格跨度

  编写一个 StockSpanner 类，它收集某些股票的每日报价，并返回该股票当日价格的跨度。

  今天股票价格的跨度被定义为股票价格小于或等于今天价格的最大连续日数（从今天开始往回数，包括今天）。

  例如，如果未来7天股票的价格是 [100, 80, 60, 70, 60, 75, 85]，那么股票跨度将是 [1, 1, 1, 2, 1, 4, 6]。

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29

  class StockSpanner { public: StockSpanner() { //插入最初的值 st.emplace(pair<int,int>{-1,INT_MAX}); m_ind = -1; } int next(int price) { //使用单调栈，单调减 while(price>=st.top().second){ st.pop(); } //当前数的下标 ++m_ind; int ret = m_ind - st.top().first; st.emplace(pair<int,int>{m_ind,price}); return ret; } private: stack<pair<int,int>> st; int m_ind; }; /** * Your StockSpanner object will be instantiated and called as such: * StockSpanner* obj = new StockSpanner(); * int param_1 = obj->next(price); */

脑筋急转弯

• 6131. 不可能得到的最短骰子序列

  给你一个长度为 n 的整数数组 rolls 和一个整数 k 。你扔一个 k 面的骰子 n 次，骰子的每个面分别是 1 到 k ，其中第 i 次扔得到的数字是 rolls[i] 。

  请你返回 无法 从 rolls 中得到的 最短 骰子子序列的长度。

  扔一个 k 面的骰子 len 次得到的是一个长度为 len 的 骰子子序列 。

  注意 ，子序列只需要保持在原数组中的顺序，不需要连续。

  示例 1：

  1 2 3 4 5 6

  输入：rolls = [4,2,1,2,3,3,2,4,1], k = 4 输出：3 解释：所有长度为 1 的骰子子序列 [1] ，[2] ，[3] ，[4] 都可以从原数组中得到。 所有长度为 2 的骰子子序列 [1, 1] ，[1, 2] ，... ，[4, 4] 都可以从原数组中得到。 子序列 [1, 4, 2] 无法从原数组中得到，所以我们返回 3 。 还有别的子序列也无法从原数组中得到

• 思路：因为是k位的所有排列，所有可以遍历数组。不妨考虑一下，在我们已经找到了所有长度为t的所有排列时，怎样才能找到所有长度为t+1的排列？

• 结论是：当且仅当在已经使用过的序列之后，还能找到1~k的所有数，这样就能形成所有排列 比如示例rolls = [4,2,1,2,3,3,2,4,1], k = 4中，就有[4,2,1,3],[3,2,4,1]两个完整的子序列，则3就是最小的找不到的序列 因此题目可以转化为能形成多少个互不交叉的完整的序列(不必有序)

• 使用哈希表记录找到的个数即可

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

  class Solution { public: int shortestSequence(vector<int>& rolls, int k) { int n = rolls.size(); int i=0; int step = 1; for(;i<n;){ unordered_set<int> us; while(i<n&&us.size()<k){ us.insert(rolls[i]); ++i; } if(us.size()==k){ ++step; } } return step; } };

• 6127. 优质数对的数目

  给你一个下标从 0 开始的正整数数组 nums 和一个正整数 k 。

  如果满足下述条件，则数对 (num1, num2) 是 优质数对 ：

  • num1 和 num2 都 在数组 nums 中存在。
  • num1 OR num2 和 num1 AND num2 的二进制表示中值为 1 的位数之和大于等于 k ，其中 OR 是按位 或 操作，而 AND 是按位 与 操作。

  返回 不同 优质数对的数目。

  如果 a != c 或者 b != d ，则认为 (a, b) 和 (c, d) 是不同的两个数对。例如，(1, 2) 和 (2, 1) 不同。

  **注意：**如果 num1 在数组中至少出现 一次 ，则满足 num1 == num2 的数对 (num1, num2) 也可以是优质数对。

• 注意num1 OR num2 和 num1 AND num2 的二进制表示中值为 1 的位数之和，其实就是num1的1的位数+num2的位数。这个是解题关键！

• 然后就是代码的一些优化，去重操作，如何计算二进制1的次数。可以使用库函数__builtin_popcount(i)。也可以自己写。

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

  class Solution { public: using ll = long long; long long countExcellentPairs(vector<int>& nums, int k) { unordered_set<int> us(nums.begin(),nums.end());//去除重复的元素,多个1只能当成是1个1 unordered_map<int,int> cnt; for(auto &i:us){ int cc = __builtin_popcount(i);//计算二进制1的位数 cnt[cc]++;//当成位数为cc的次数，用于乘法准则 } ll ans = 0L; for(auto &[x,cx]:cnt){ for(auto &[y,cy]:cnt){ if(x+y>=k){ ans += cx*cy; } } } return ans; } };

• 自己写位数函数

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32

  class Solution { public: using ll = long long; //计算1的位数，n&(n-1) int num1c(int i){ int cnt = 0; while(i){ i = i&(i-1); ++cnt; } return cnt; } long long countExcellentPairs(vector<int>& nums, int k) { unordered_set<int> us(nums.begin(),nums.end());//去除重复的元素,多个1只能当成是1个1 unordered_map<int,int> cnt; for(auto &i:us){ int cc = num1c(i);//计算二进制1的位数 cnt[cc]++;//当成位数为cc的次数，用于乘法准则 } ll ans = 0L; for(auto &[x,cx]:cnt){ for(auto &[y,cy]:cnt){ if(x+y>=k){ ans += cx*cy; } } } return ans; } };

• 使用后缀和优化双重for循环，相当于多一个备忘录，减少计算次数，优化时间复杂度

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23

  class Solution { static constexpr int U = 30; public: long long countExcellentPairs(vector<int> &nums, int k) { int cnt[U] = {0};//初始化为0，最多29位，因为10^9 for (int x : unordered_set<int>(nums.begin(), nums.end())) // 去重 cnt[__builtin_popcount(x)]++; long ans = 0L; int s = 0; //计算后缀和 for (int i = k; i < U; ++i) s += cnt[i]; for (int cx = 0; cx < U; ++cx) { ans += (long) cnt[cx] * s; // 更新后缀和 int cy = k - 1 - cx; if (0 <= cy && cy < U) { s += cnt[cy]; } } return ans; } };

• 593. 有效的正方形

  给定2D空间中四个点的坐标 p1, p2, p3 和 p4，如果这四个点构成一个正方形，则返回 true 。

  点的坐标 pi 表示为 [xi, yi] 。输入 不是 按任何顺序给出的。

  一个 有效的正方形 有四条等边和四个等角(90度角)。

• 思路：一般证明是正方形，是通过边或角证明的，初中证明题。

  • 四条边相等证明是菱形，两条对角线相等，证明是正方形。
  • 四个等腰直角三角形。
  • 证明是平行四边形+矩形+正方形。

• 采取前两个思路比较简单

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27

  class Solution { public: using ll = long long; //采用方法1，只有两种长度 bool validSquare(vector<int>& p1, vector<int>& p2, vector<int>& p3, vector<int>& p4) { vector<ll> dis; dis.push_back(pow(p1[0]-p2[0],2)+pow(p1[1]-p2[1],2)); dis.push_back(pow(p2[0]-p3[0],2)+pow(p2[1]-p3[1],2)); dis.push_back(pow(p3[0]-p4[0],2)+pow(p3[1]-p4[1],2)); dis.push_back(pow(p2[0]-p4[0],2)+pow(p2[1]-p4[1],2)); dis.push_back(pow(p3[0]-p1[0],2)+pow(p3[1]-p1[1],2)); dis.push_back(pow(p1[0]-p4[0],2)+pow(p1[1]-p4[1],2)); unordered_set<ll> us; for(auto &i:dis){ // 等于0 表示同一个点 if(i==0){ return false; } us.insert(i); } if(us.size()==2){ return true; }else{ return false; } } };

• 6133. 分组的最大数量

  给你一个正整数数组 grades ，表示大学中一些学生的成绩。你打算将 所有 学生分为一些 有序 的非空分组，其中分组间的顺序满足以下全部条件：

  • 第 i 个分组中的学生总成绩 小于 第 (i + 1) 个分组中的学生总成绩，对所有组均成立（除了最后一组）。
  • 第 i 个分组中的学生总数 小于 第 (i + 1) 个分组中的学生总数，对所有组均成立（除了最后一组）。

  返回可以形成的 最大 组数。

• 思路1：排序+贪心模拟

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45

  class Solution { public: using ll = long long; int maximumGroups(vector<int>& grades) { //贪心 sort(grades.begin(),grades.end()); int ans = 1; ll curr = (ll)grades[0]; int len = grades.size(); int i = 0; while(i<len){ ++ans; int left = i; int rigth = i+ans; if(rigth>=len){ return --ans; break; } ll sum = 0; for(int j =left+1;j<=rigth;++j){ sum +=grades[j]; } if(sum>curr){ curr = sum; i = rigth; }else{ int idx = rigth+1; while(idx<len){ sum +=grades[idx]; ++idx; if(sum>curr){ break; } } if(sum>curr){ curr = sum; i = idx-1; }else{ return --ans; } } } return ans; } };

• 思路2：和贪心没有一点关系，只要符合1+2+3+4+..+n，就能分n组。等差数列公式计算

• 1 2 3 4 5 6 7 8 9 10 11 12

  class Solution { public: int maximumGroups(vector<int>& grades) { //跟贪心没半毛钱关系 int ans = 1, len = grades.size(); for(int i=1;i*(i+1)<=2*len;++i){ ans = i; } return ans; } };

预处理左右下标+数学

• 828. 统计子串中的唯一字符

  我们定义了一个函数 countUniqueChars(s) 来统计字符串 s 中的唯一字符，并返回唯一字符的个数。

  例如：s = "LEETCODE" ，则其中 "L", "T","C","O","D" 都是唯一字符，因为它们只出现一次，所以 countUniqueChars(s) = 5 。

  本题将会给你一个字符串 s ，我们需要返回 countUniqueChars(t) 的总和，其中 t 是 s 的子字符串。输入用例保证返回值为 32 位整数。

  注意，某些子字符串可能是重复的，但你统计时也必须算上这些重复的子字符串（也就是说，你必须统计 s 的所有子字符串中的唯一字符）。

• 思路1：乘法原理+数学

• 

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28

  class Solution { public: int uniqueLetterString(string s) { int n = s.size(); int pre[26]; memset(pre, -1, sizeof(pre)); vector<int> last(26,n); vector<int> left(n,-1); vector<int> right(n,n); //记录左侧 for(int i = 0;i<n;++i){ int idx = s[i] - 'A'; left[i] = pre[idx]; pre[idx] = i; } //记录右侧 for(int i = n-1;i>=0;--i){ int idx = s[i] - 'A'; right[i] = last[idx]; last[idx] = i; } int ans = 0; for(int i = 0;i<n;++i){ ans+=(i-left[i])*(right[i]-i); } return ans; } };

单调栈模板

• 若是计算右边严格小于当前元素的第一个元素，采用单调增的栈。

  • 当元素小于栈顶元素，栈顶元素出栈，记录映射，继续循环；

  • 否则当前元素入栈

  • 1 2 3 4 5 6 7

    for(int i = 0;i<n;++i){ while(st.size()&&arr[i]<arr[st.top()]){ right[st.top()] = i; st.pop(); } st.emplace(i); }

• 1 2 3 4 5 6 7

  for(int i = n-1;i>=0;--i){ while(st.size()&& heights[st.top()]>heights[i]){ left[st.top()] = i; st.pop(); } st.emplace(i); }

• 907. 子数组的最小值之和

  给定一个整数数组 arr，找到 min(b) 的总和，其中 b 的范围为 arr 的每个（连续）子数组。

  由于答案可能很大，因此 返回答案模 10^9 + 7 。

• 

• 思路就是：预处理左右数组，使用单调栈计算右边第一个严格小于当前元素的元素的位置；左边第一个小于等于当前元素的元素的位置。

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38

  class Solution { public: const int mod = 1000000007; int sumSubarrayMins(vector<int>& arr) { int n = arr.size(); vector<int> left(n,-1); vector<int> right(n,n); //单调栈求左右两边第一个小的，left严格小于，rigght小于等于 stack<int> st; //先求右边, 求小于，则是单调增的栈;最后如果栈非空，说明没有小于的，取默认的n for(int i = 0;i<n;++i){ while(st.size()&&arr[i]<arr[st.top()]){ right[st.top()] = i; st.pop(); } st.emplace(i); } //再求左边，小于等于 while(st.size()){ st.pop(); } for(int i = n-1;i>=0;--i){ while(st.size()&&arr[i]<=arr[st.top()]){ left[st.top()] = i; st.pop(); } st.emplace(i); } long long ans =0; for(int i = 0;i<n;++i){ long long tmp1 = i-left[i]; long long tmp2 = right[i] - i; ans += arr[i]*tmp1*tmp2; ans = ans%mod; } return (int)ans; } };

字符串总引力/ 统计子串的唯一字符

• 2262. 字符串的总引力

  字符串的 引力 定义为：字符串中 不同 字符的数量。

  • 例如，"abbca" 的引力为 3 ，因为其中有 3 个不同字符 'a'、'b' 和 'c' 。

  给你一个字符串 s ，返回 其所有子字符串的总引力 。

  子字符串 定义为：字符串中的一个连续字符序列。

• 

• 

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

  class Solution { public: using ll = long long; long long appealSum(string s) { int n = s.size(); int idx[26]; memset(idx,-1,sizeof(idx)); ll total = 0L; ll res = 0L; for(int i = 0;i<n;++i){ int tmp = s[i]-'a'; total += i-idx[tmp]; res += total; idx[tmp] = i; } return res; } };

• 828. 统计子串中的唯一字符

  我们定义了一个函数 countUniqueChars(s) 来统计字符串 s 中的唯一字符，并返回唯一字符的个数。

  例如：s = "LEETCODE" ，则其中 "L", "T","C","O","D" 都是唯一字符，因为它们只出现一次，所以 countUniqueChars(s) = 5 。

  本题将会给你一个字符串 s ，我们需要返回 countUniqueChars(t) 的总和，其中 t 是 s 的子字符串。输入用例保证返回值为 32 位整数。

  注意，某些子字符串可能是重复的，但你统计时也必须算上这些重复的子字符串（也就是说，你必须统计 s 的所有子字符串中的唯一字符）。

• 思路2：在预处理左右数组的前提下使用数学计算优化空间，我称之为DP的优化。

• 

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21

  class Solution { public: int uniqueLetterString(string s) { int n = s.size(); int last0[26];//上一次字母的位置 int last1[26];//上上次字母的位置 //初始化都为-1 memset(last0,-1,sizeof(last0)); memset(last1,-1,sizeof(last1)); int total = 0, ans = 0; for(int i = 0;i<n;++i){ int curr = s[i]-'A'; total += i-(2*last0[curr])+last1[curr]; ans += total; //更新 last1[curr] = last0[curr]; last0[curr] = i; } return ans; } };

卡塔兰数

• 参考

• 96. 不同的二叉搜索树

  给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

• 思路1：使用动态规划，dp的含义是第i个节点组成的二叉搜索树的个数。

• 递推公式：以1为根节点+以2为根节点+。。。+以n为根节点的数的和。

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14

  class Solution { public: int numTrees(int n) { vector<int> dp(n+1,0); dp[0] = 1; dp[1] = 1; for(int i = 2;i<=n;++i){ for(int j = 1;j<=i;++j){ dp[i] += dp[j-1]*dp[i-j]; } } return dp[n]; } };

• 思路2：数学证明

• 

• 1 2 3 4 5 6 7 8 9 10 11

  class Solution { public: int numTrees(int n) { using ll = long long; ll C=1; for(int i=0;i<n;++i){ C = C*2*(2*i+1)/(i+2); } return C; } };

• 思考3：组合数学

• 

• 1049. 最后一块石头的重量 II

  有一堆石头，用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。

  每一回合，从中选出任意两块石头，然后将它们一起粉碎。假设石头的重量分别为 x 和 y，且 x <= y。那么粉碎的可能结果如下：

  • 如果 x == y，那么两块石头都会被完全粉碎；
  • 如果 x != y，那么重量为 x 的石头将会完全粉碎，而重量为 y 的石头新重量为 y-x。

  最后，最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下，就返回 0。

• 思路：分割等和子集的进阶版，脑筋急转弯+dp

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29

  class Solution { public: int lastStoneWeightII(vector<int>& stones) { //脑筋急转弯 //问题转换为分为左右重量最接近的两半，然后对撞粉碎，得出最小重量 //分割等和子集的进阶版 int sum = accumulate(stones.begin(), stones.end(), 0); int len = sum/2; vector<bool> dp(len+1,false); dp[0] = true; for(int &stone:stones){ if(stone>len){ continue; } for(int i = len;i>=stone;--i){ dp[i] = dp[i] || dp[i-stone]; } } int ans=0; for(int i = len;i>=0;--i){ if(dp[i]){ ans = i; break; } } return sum-2*ans; } };

• 899. 有序队列

  给定一个字符串 s 和一个整数 k 。你可以从 s 的前 k 个字母中选择一个，并把它加到字符串的末尾。

  返回 在应用上述步骤的任意数量的移动后，字典上最小的字符串 。

• 思路：当k=1时，只有一种移动方法，计算字符串的最小表示法——循环同构。当k>=2时，直接排序就好了，因为始终可以移动到排好序的结果，具体自己可以思考下，假设排序结果，先排最后两个，再依次排下去，类似冒泡。

• 这里循环同构采用朴素算法，直接O(N^2)。最小代表法可以降低一个数量级。

• 

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27

  class Solution { public: string orderlyQueue(string s, int k) { if(s.size()==1){ return s; } if(k==1){ //转n-1次 int n = s.size(); string ret = s; for(int i = 0;i<n;++i){ char tmp = s[0]; for(int j = 0;j<n-1;++j){ s[j] = s[j+1]; } s[n-1] = tmp; if(ret>s){ ret = s; } } return ret; }else{ sort(s.begin(),s.end()); return s; } } };

整数拆分使得乘积最大

• 343. 整数拆分

  给定一个正整数 n ，将其拆分为 k 个 正整数 的和（ k >= 2 ），并使这些整数的乘积最大化。

  返回 你可以获得的最大乘积 。

• 思路：动态规划或者数学，数学是一种脑筋急转弯（注意和质因数分解的区别）

• 2和3可以组成的所有正整数（>1）

• 未完待续

随机数洗牌算法

• 384. 打乱数组

  给你一个整数数组 nums ，设计算法来打乱一个没有重复元素的数组。

  实现 Solution class:

  • Solution(int[] nums) 使用整数数组 nums 初始化对象
  • int[] reset() 重设数组到它的初始状态并返回
  • int[] shuffle() 返回数组随机打乱后的结果

• 为什么随机一个数选取，添加新数列，然后删除这个数再随机就是概率相等呢

  • 例如3个数，第一个取概率1/3；然后删除这个，剩下两个随机一个，2/3*1/2=1/3，所有概率相等。

    1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49

    class Solution { public: vector<int> src,ret; Solution(vector<int>& nums) { src.assign(nums.begin(),nums.end()); } vector<int> reset() { return src; } vector<int> shuffle() { // //方法1，调用库函数 // ret.assign(src.begin(),src.end()); // random_shuffle(ret.begin(), ret.end()); // return ret; // //方法2，使用随机数函数rand // vector<int> temp(src.begin(),src.end()); // ret=vector<int>(temp.size());//赋予空间，不初始化 // for(int i=0;i<src.size();++i){ // int j=rand()%(temp.size()); // auto it=temp.begin()+j; // ret[i]=*it; // temp.erase(it); // } // return ret; // //方法3：使用洗牌算法1,随机数和末尾交换，前面的再随机 // ret.assign(src.begin(),src.end()); // int n=src.size(); // for(int i=0;i<n;++i){ // int j=rand()%(n-i); // swap(ret[j], ret[n-1-i]); // } // return ret; //方法4：使用洗牌算法，随机数和开头的交换，后面的再随机 ret.assign(src.begin(),src.end()); int n=src.size(); for(int i=0;i<n;++i){ int j=i+rand()%(n-i); swap(ret[j], ret[i]); } return ret; } };

• 202. 快乐数

  编写一个算法来判断一个数 n 是不是快乐数。

  「快乐数」定义为：

  • 对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。
  • 然后重复这个过程直到这个数变为 1，也可能是 无限循环 但始终变不到 1。
  • 如果 可以变为 1，那么这个数就是快乐数。

  如果 n 是快乐数就返回 true ；不是，则返回 false 。

  • 思路：

    根据我们的探索，我们不断平方和会有以下三种可能。

    1. 最终会得到 1。
    2. 最终会进入循环。
    3. 值会越来越大，最后接近无穷大。

    但是第三种情况一定不会发生，因为：

  

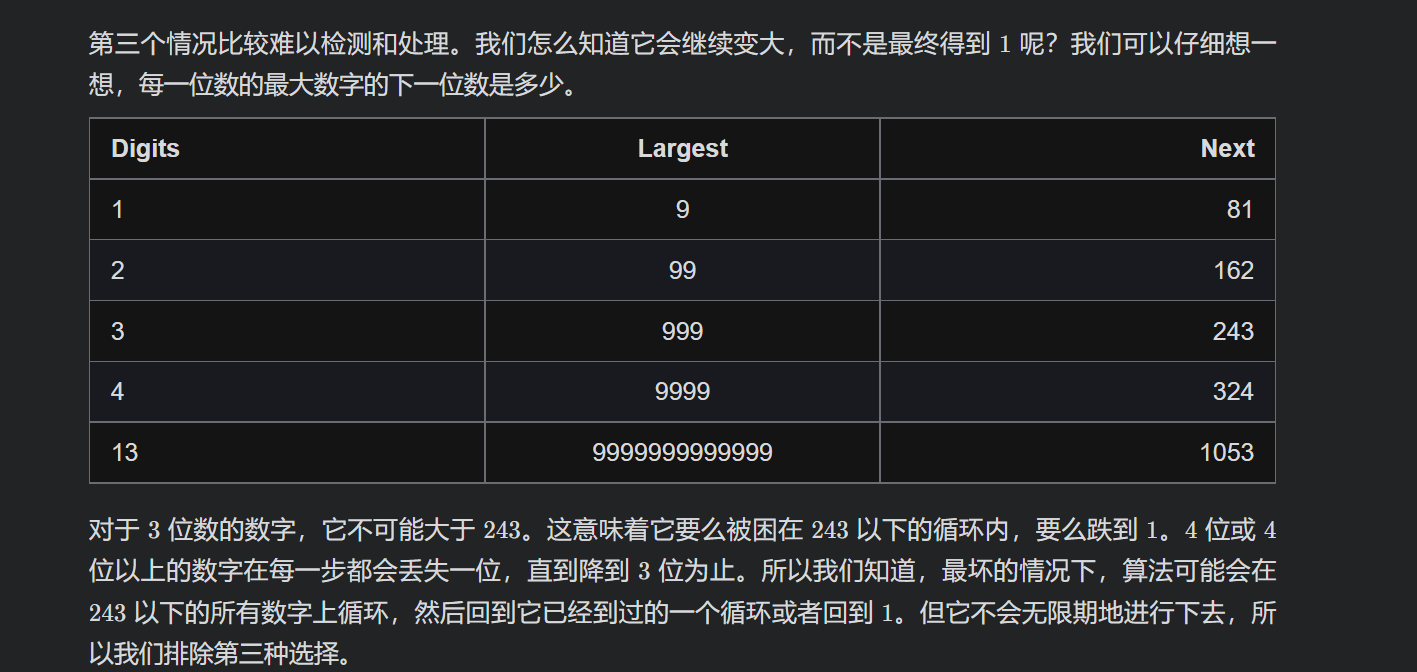
  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31

  class Solution { public: int square(int n){ int ret=0; int cur=0; while(n>0){ cur=n%10; ret+=cur*cur; n/=10; } return ret; } bool isHappy(int n) { if(n==1){ return true; } int ret=n; unordered_set<int> dp; ret=square(ret); dp.insert(ret); while(ret!=1){ ret=square(ret); if(dp.count(ret)){ return false; } dp.insert(ret); } return true; } };

• 思路2：使用快慢指针

• 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

  class Solution { public: using ll = long long; ll digital(ll n){ ll ret = 0; while(n>0){ ll tmp = n%10; ret += tmp*tmp; n = n/10; } return ret; } bool isHappy(int n) { //没必要判断起点，判断入圈就好 ll fastNode = n; ll slowNode = n; do{ if(fastNode ==1){ return true; } slowNode = digital(slowNode); fastNode = digital(digital(fastNode)); }while(fastNode!=slowNode); if(fastNode==1){ return true; } return false; } };

• 149. 直线上最多的点数思路

  给你一个数组 points ，其中 points[i] = [xi, yi] 表示 X-Y 平面上的一个点。求最多有多少个点在同一条直线上。

  • 细节题
    • 使用哈希表记录斜率个数
    • 不能使用浮点数记录斜率
    • 最大公约数的算法——辗转相除法

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48

  class Solution { public: //求最大公约数，辗转相除法,不需要特别输出a、b哪个数大，即使a<b，一次辗转相除之后就会转换位置，然后也依次类推，知道余数等于0，输出除数 int gcd(int a, int b) { return b==0 ? a:gcd(b, a % b) ; } int maxPoints(vector<vector<int>>& points) { int n = points.size(); if (n <= 2) { return n; } int ret = 0; //依次计算每个点的所有斜率 for (int i = 0; i < n; i++) { //过半的点或者大于剩下的数的点的斜率，就已经是最大的了，优化步骤 if (ret >= n - i || ret > n / 2) { break; } unordered_map<int, int> mp; for (int j = i + 1; j < n; j++) { int x = points[i][0] - points[j][0]; int y = points[i][1] - points[j][1]; if (x == 0) { y = 1;//竖线 } else if (y == 0) { x = 1;//横线 } else { if (y < 0) {//规定分子都大于0 x = -x; y = -y; } int gcdXY = gcd(abs(x), abs(y)); x /= gcdXY, y /= gcdXY; } //因为本题的范围<10的4 mp[y + x * 20001]++; } int maxn = 0; for (auto& i : mp) { maxn = max(maxn, i.second + 1); } ret = max(ret, maxn); } return ret; } };

扫描线模板

• 850. 矩形面积 II

  我们给出了一个（轴对齐的）二维矩形列表 rectangles 。 对于 rectangle[i] = [x1, y1, x2, y2]，其中（x1，y1）是矩形 i 左下角的坐标， (xi1, yi1) 是该矩形 左下角 的坐标， (xi2, yi2) 是该矩形 右上角 的坐标。

  计算平面中所有 rectangles 所覆盖的 总面积 。任何被两个或多个矩形覆盖的区域应只计算 一次 。

  返回 总面积 。因为答案可能太大，返回 109 + 7 的 模 。

• 个人觉得难点是如何维护[覆盖的线段长度]，题解都看不懂！

• 待续

迷宫生成算法

• 待续