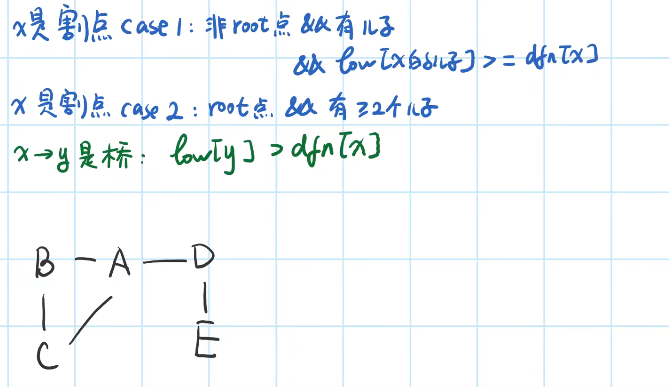绪论
-
七桥问题:一次性走完七座桥。
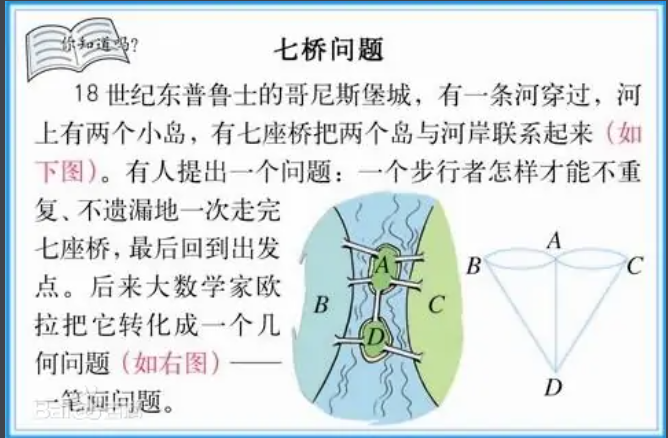
欧拉证明是不可能的,因为该图中每一个顶点都和奇数条边相连。(边就是桥,顶点是ABC)
基本定义
-
顶点:在上面的七桥问题中,小 A 、小 B 、小 C 等均称为「图」的顶点。用集合
V表示。Vertex: 顶点 -
边:顶点之间的连接线称为边。用
E这个集合表示。Edge: 边缘 -
路径:从一个顶点到另一个顶点之间经过的所有顶点的集合。注意:**两个顶点之间的路径可以是很多条。
-
路径长度:一条路径上经过的边的数量。
-
连通性:两个不同顶点之间存在至少一条路径,则称这两个顶点是连通的。
-
环:起点和终点为同一个顶点的路径。
-
负权环:在加权图中,如果一个环的所有边的权重加起来为负数,我们就称之为负权环。
-
表示方法:
-
邻接列表:在邻接列表实现中,每一个顶点会存储一个从它这里开始的边的列表。比如,如果顶点A 有一条边到B、C和D,那么A的列表中会有3条边
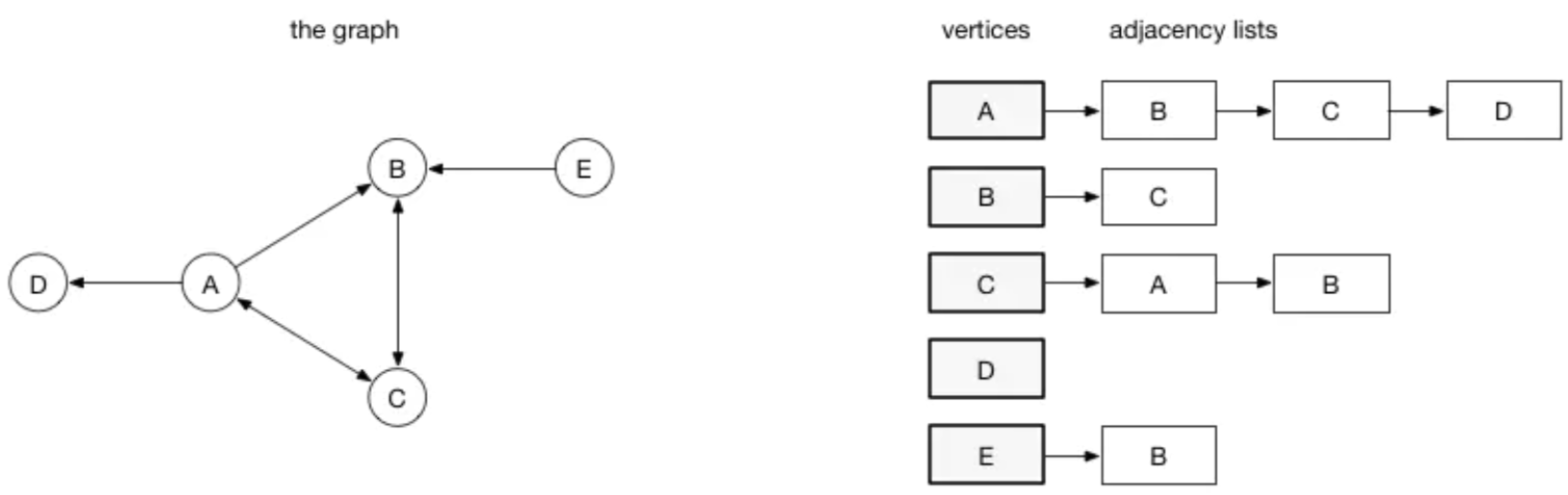
-
邻接矩阵:在邻接矩阵实现中,由行和列都表示顶点,由两个顶点所决定的矩阵对应元素表示这里两个顶点是否相连、如果相连这个值表示的是相连边的权重。例如,如果从顶点A到顶点B有一条权重为 5.6 的边,那么矩阵中第A行第B列的位置的元素值应该是5.6:

-
无向图
- 连通图(一般都是指无向图):如果图中任意俩顶点都连通,则该图为连通图。
- 连通分量:与连通图对应,一般书上说的都是特指无向图。极大连通子图是无向图的连通分量。(暗指极大连通子图也指无向图)。
- 顶点的度:「度」适用于无向图,指的是和该顶点相连接的所有边数称为顶点的度。
有向图
- 强连通图(特指有向图):在有向图中,若都存在从顶点v到m和从顶点m到v的双向路径,则称这俩顶点时强连通的。若任意一对顶点都是强连通的,称此图为强连通图。
- 强连通分量:有向图中的极大强连通子图称为有向图的强连通分量。
- 弱连通图:将有向图的所有的有向边替换为无向边,所得到的图称为原图的基图。如果一个有向图的基图是连通图,则有向图是弱连通图。
- 弱连通分量:有向图中的极大弱连通子图称为有向图弱连通分量。
- 顶点的入度:「入度」适用于有向图,一个顶点的入度为d,则表示有d条与顶点相连的边指向该顶点。
- 顶点的出度:「出度」适用于有向图,它与「入度」相反。一个顶点的出度为d,则表示有d条与顶点相连的边以该顶点为起点。
生成树
-
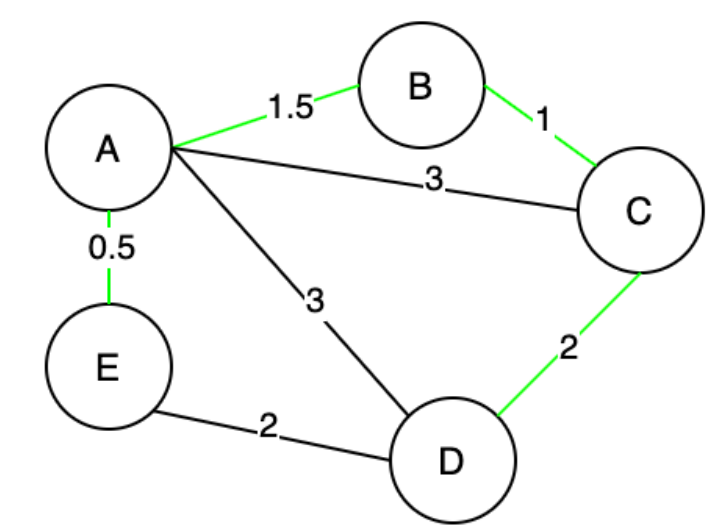
生成树:一个连通图(特指无向图)的最小连通子图称作该图的生成树。有n个顶点的连通图的生成树有n个顶点和n - 1条边。生成树指的是「无向图」中,具有该图的 全部顶点且边数最少的连通子图。下图中,所有粉色线条组成的一棵树[(A, B), (A, C), (A, D), (A, E)],就是该无向图的其中一个生成树。其实[(A, E),(A, B), (B, C), (C, D)]也是该无向图的一个生成树。由此可见,一个「无向图」的生成树可以是多个。

-
最小生成树:最小生成树指的是「加权无向图」中总权重最小的生成树。下图中,所有绿色线条组成的一颗生成树[(A, E),(A, B), (B, C), (C, D)],就是该加权无向图的其中一个最小生成树。其实[(A, E), (E, D), (A, B), (B, C)]也是该加权无向图的另一个最小生成树,由此可见,一个「加权无向图」的最小生成树可以是多个。
并查集
- 用于判断无向图的连通性,以及计算连通分量的个数。
图的深度优先搜索算法
-
在前面的「并查集」数据结构中,大家已经知道如何检查两个顶点之间的连通性。那如果给你一个「图」,你该如何找出它所有的顶点呢?以及你又如何找出它两个顶点之间的所有路径呢?此时,「深度优先搜索」算法就可以登场了。
-
「深度优先搜索」(又称「Depth First Search」,简称「DFS」)算法在「图」中主要用途:
- 遍历「图」中所有顶点;
- 遍历「图」中任意两点之间的所有路径。
-
数据结构——
stack栈,用于回退。一般不会直接使用栈,一般使用递归回溯,即隐性的使用了栈。
遍历图的所有顶点
-
栈里面放顶点。
-
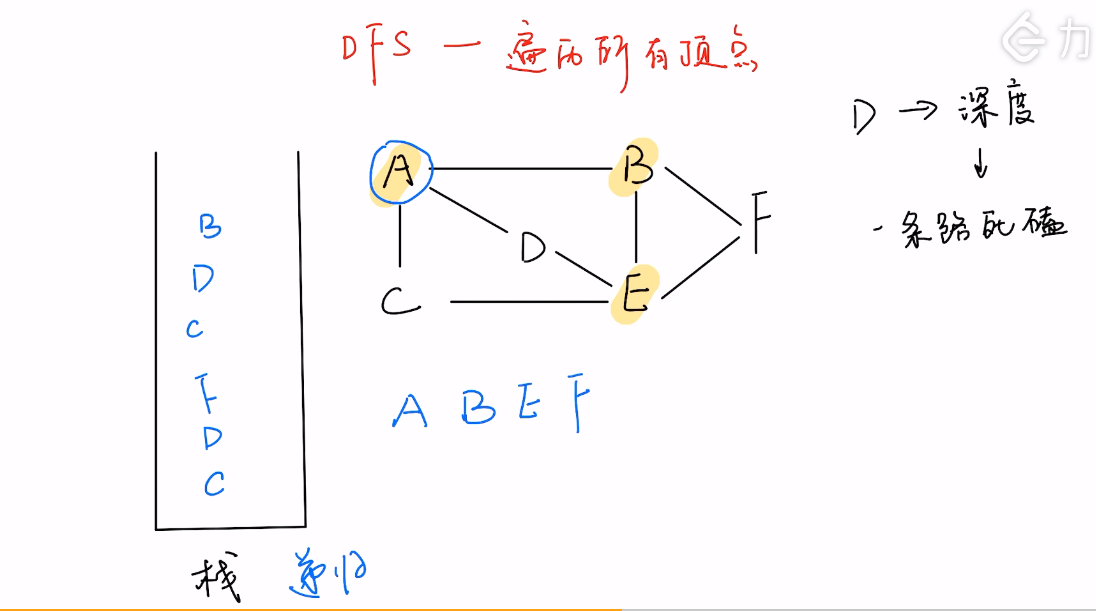
-
时间复杂度:$O(V+E)$,其中V表示顶点数,E表示边数。
-
空间复杂度:$O(V)$,V表示顶点数。
遍历两点之间的所有路径
-
栈里面放边。
-
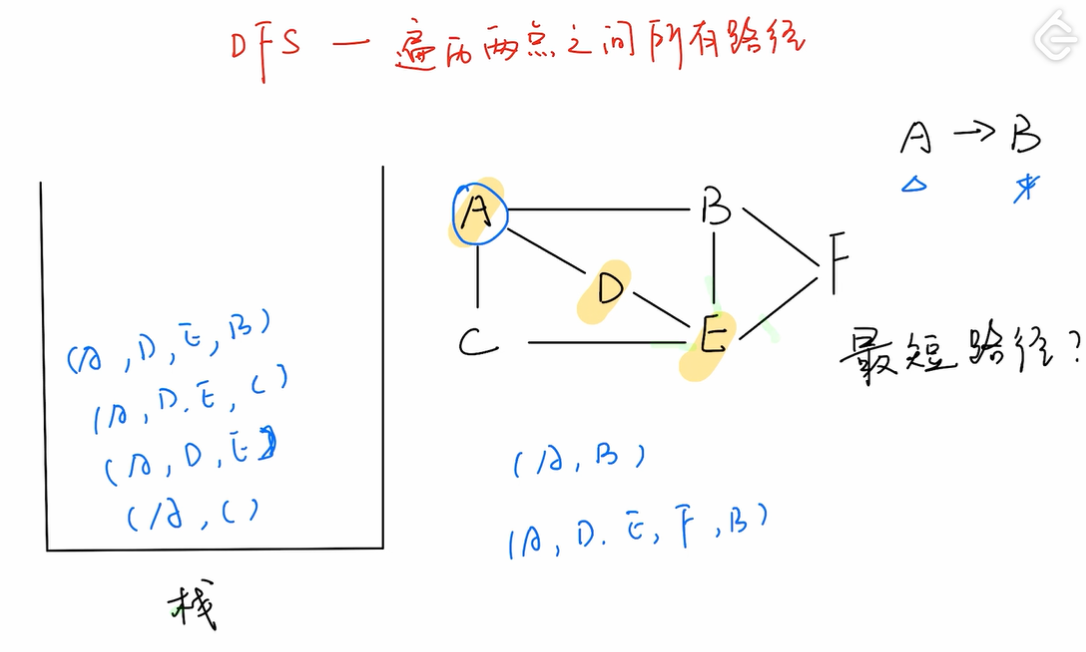
-
时间复杂度:$O((2^V)*(V+E))$,其中V表示顶点数,E表示边数。
-
空间复杂度:$O((2^V)*V)$,其中V表示顶点数。
DFS遍历示例
-
思路:类似回溯,但区别是,回溯的撤回操作在for循环里面;无向图遍历的撤回在for循环外面。
-
回溯代码模板
1 2 3 4 5 6 7 8 9 10 11 12 13//一般无返回值,backtracking函数纵向搜索,for循环横向搜索。 void backtracking(路径,选择列表) { if (终止条件) { 存放结果; return; } for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) { 处理节点; backtracking(路径,选择列表); // 递归 回溯,撤销处理结果 } } -
一般需要visited数组标记信息。以防重复遍历。
-
在 for 循环里面和外面唯一的区别就是对根节点的处理。
比如下面两种多叉树的遍历:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29//撤回在for循环外面,会打印包括根节点的所有信息 void traverse(TreeNode *root) { if (!root) { return; } cout << root->val << endl;//处理节点 for (auto &i : root.children) { traverse(i); } cout << root->val << endl;//撤销节点 } //撤回在for循环里面,会缺少整棵树的根节点的进入和离开信息,和回溯代码模板很像 void traverse_2(TreeNode *root) { if (!root) { return; } for (auto &i : root.children) { cout << "child" << root->val << endl;//处理节点 traverse(i); cout << "child" << root->val << endl;//撤销节点 } } -
为什么回溯算法框架会用后者?因为回溯算法关注的不是节点,而是树枝。参考下图。
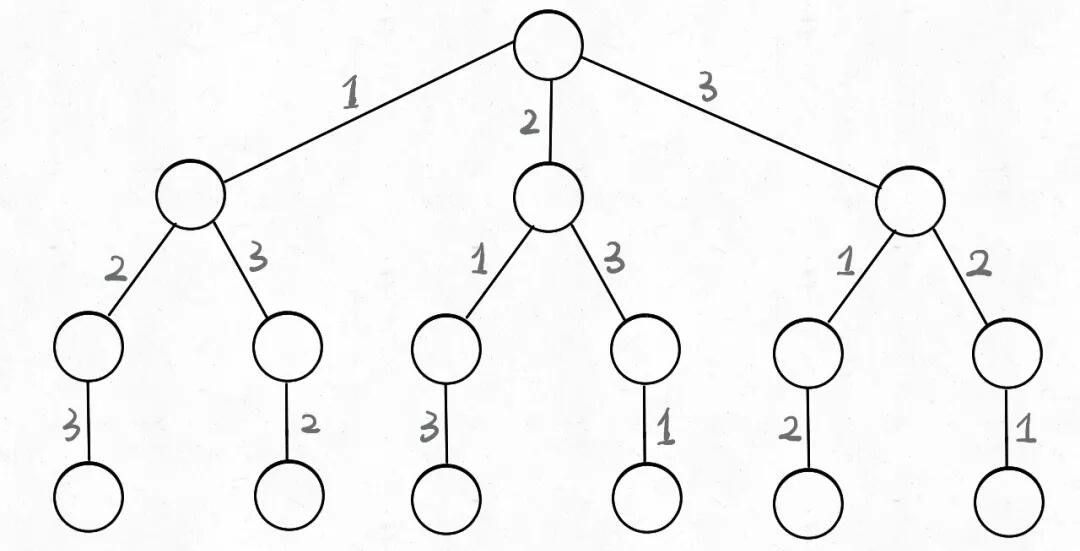
-
无向图遍历模板
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27vector<vector<int>> ret; vector<int> path; void dfs(vector<vector<int>>& graph, vector<bool> &visited, int start){ if(visited[start]){ return; } //终止条件 if(start==graph.size()-1){ path.push_back(start); ret.push_back(path); path.pop_back(); return; } //处理节点 path.push_back(start); visited[start]=true; //递归 for(auto &i:graph[start]){ dfs(graph,visited,i); } //回溯,撤回 path.pop_back(); visited[start]=false; } -
给你一个有
n个节点的 有向无环图(DAG),请你找出所有从节点0到节点n-1的路径并输出(不要求按特定顺序)二维数组的第
i个数组中的单元都表示有向图中i号节点所能到达的下一些节点,空就是没有下一个结点了。译者注:有向图是有方向的,即规定了 a→b 你就不能从 b→a 。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39class Solution { public: vector<vector<int>> ret; vector<int> path; void dfs(vector<vector<int>>& graph, vector<bool> &visited, int start){ if(visited[start]){ return; } //终止条件 if(start==graph.size()-1){ path.push_back(start); ret.push_back(path); path.pop_back(); return; } //处理节点 path.push_back(start); visited[start]=true; //递归 for(auto &i:graph[start]){ dfs(graph,visited,i); } //回溯,撤回 path.pop_back(); visited[start]=false; } vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) { ret.clear(); path.clear(); int n=graph.size(); vector<bool> visited(n,false); dfs(graph, visited, 0); return ret; } };
图的广度优先搜索算法
-
「广度优先搜索」算法不仅可以遍历「图」的所有顶点,也可以遍历两个顶点的所有路径。但是,「广度优先搜索」最高效的用途是:当在权重相等且均为正数的「图」 中,它可以快速的找到两点之间的最短路径。
-
「广度优先遍历」(又称「Breath First Search」,简称「BFS」)算法在「图」中主要用途:
- 遍历「图」中所有顶点;
- 针对权重相等且均为正数的「图」,快速找出两点之间的最短路径。
-
数据结构——队列
queue,先进先出,层层
遍历图的所有顶点
-
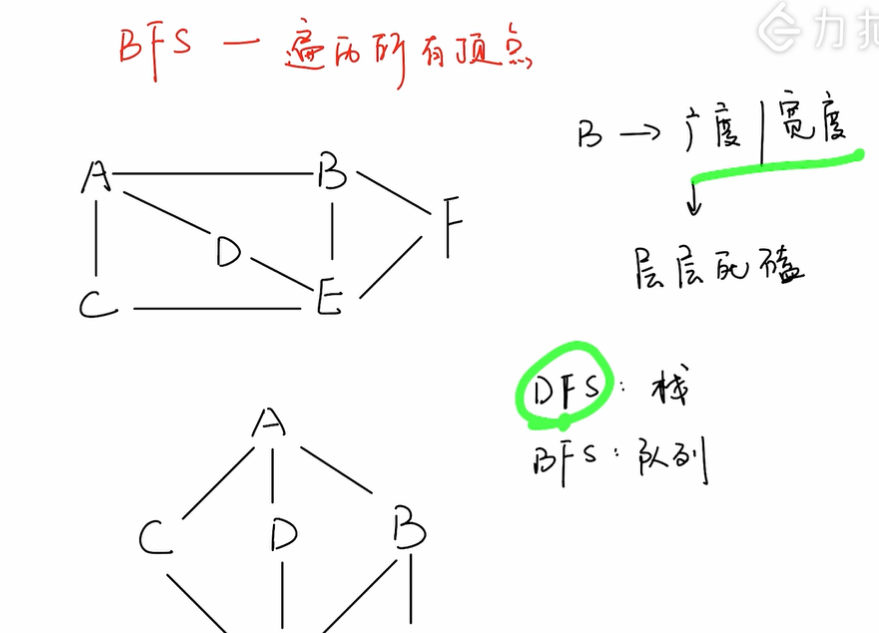
-
时间复杂度:$O(V+E)$,其中V表示顶点数,E表示边数。
-
空间复杂度:$O(V)$,V表示顶点数。
求两顶点之间的最短路径
-
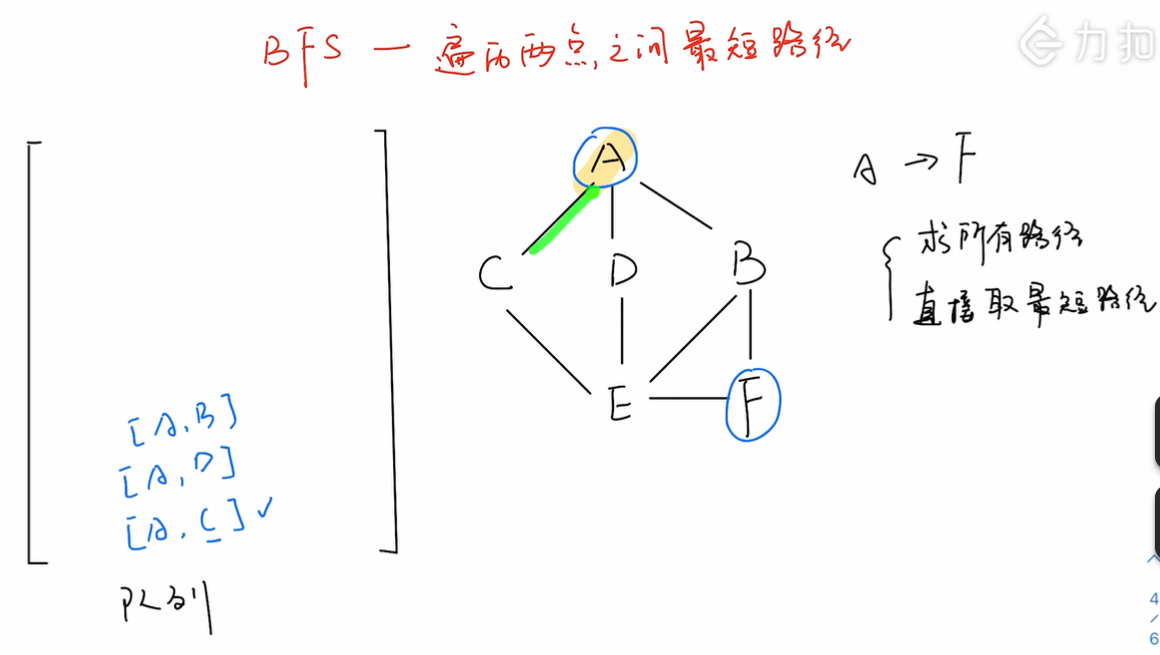
-
时间复杂度:$O(V+E)$,其中V表示顶点数,E表示边数。
-
空间复杂度:$O(V)$,V表示顶点数。
BFS遍历示例
-
给你一个有
n个节点的 有向无环图(DAG),请你找出所有从节点0到节点n-1的路径并输出(不要求按特定顺序)graph[i]是一个从节点i可以访问的所有节点的列表(即从节点i到节点graph[i][j]存在一条有向边)。 -
思路:设置
queue<vector<int>> bfs进行BFS遍历。相对来说比DFS好写一点。1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32class Solution { public: vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) { vector<vector<int>> ret; vector<int> path; queue<vector<int>> bfs; path.push_back(0); for(auto &i:graph[0]){ path.push_back(i); bfs.push(path); path.pop_back(); } int end_num=graph.size()-1; while(!bfs.empty()){ auto temp=bfs.front(); bfs.pop(); if(temp.back()==end_num){ ret.push_back(temp); continue; } auto temp2=graph[temp.back()]; if(!temp2.empty()){ for(auto &i:temp2){ temp.push_back(i); bfs.push(temp); temp.pop_back(); } } } return ret; } };
最小生成树相关算法
切分定理
-
两个基本概念
-
切分:将「图」切成两个部分,称之为一个「切分」。下面的切分图就是一个「切分」,其中(B, A, E)为一个部分,(C, D)为另外一个部分。
-
横切边:如果一条边连接的两个顶点属于切分的两个部分,这个边称为「横切边」。在切分图中,(B, C), (A, C), (A, D), (E, D) 均为「横切边」。
切分图 -
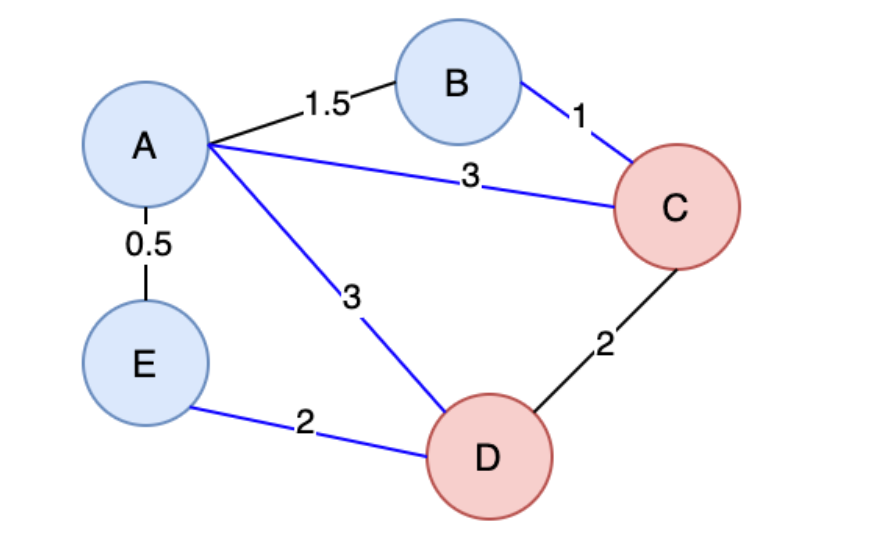
-
切分定理是 Kruskal 算法和 Prim 算法的重要的理论支撑。那么什么是「切分定理」呢?根据 维基百科 的定义,「切分定理」指的是:
在一幅连通加权无向图中,给定任意的切分,如果有一条横切边的权值严格小于所有其他横切边,则这条边必然属于图的最小生成树中的一条边。
- 两个关键词——任意切分、严格小于
Kruskal算法
基本理论
- Kruskal算法是一种用来查找最小生成树的算法,是一种贪心算法的应用。克鲁斯克尔算法。
- 步骤
-
- 新建图G,G 中拥有原图中相同的节点,但没有边。
-
- 将原图中所有的边按权值从小到大排序。
-
- 从权值最小的边开始,如果这条边连接的两个节点于图G 中不在同一个连通分量中(是否形成一个环,形成就跳过到下一条边),则添加这条边到图G中。
-
- 重复3,直至图G中所有的节点都在同一个连通分量中,即添加n-1条边,n为节点个数。
-
- 证明
- 为什么这一定是最小生成树呢?关键还是步骤3中对边的选取。算法中总共选取了n-)条边,每条边在选取的当时,都是连接两个不同的连通分量的权值最小的边。
- 要证明这条边一定属于最小生成树,可以用反证法:如果这条边不在最小生成树中,它连接的两个连通分量最终还是要连起来的,通过其他的连法,那么另一种连法与这条边一定构成了环,而环中一定有一条权值大于这条边的边,用这条边将其替换掉,图仍旧保持连通,但总权值减小了。也就是说,如果不选取这条边,最后构成的生成树的总权值一定不会是最小的。
- 时间复杂度:$O(ElogE)$,E为边数。
- 空间复杂度:$O(V)$,V表示顶点数。
示例
-
给你一个
points数组,表示 2D 平面上的一些点,其中points[i] = [xi, yi]。连接点
[xi, yi]和点[xj, yj]的费用为它们之间的 曼哈顿距离 :|xi - xj| + |yi - yj|,其中|val|表示val的绝对值。请你返回将所有点连接的最小总费用。只有任意两点之间 有且仅有 一条简单路径时,才认为所有点都已连接。
- 思路:创建边Edge 类,创建并查集UnionFind 类,同时注意排序算法,慎重加等号
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91//边 class Edge{ public: int start; int end; int cost; Edge(int start1 ,int end1, int cost1):start(start1),end(end1),cost(cost1){ } }; //并查集 class UnionFind{ public: vector<int> parent; UnionFind(int n){ parent.resize(n); //iota(parent.begin(),parent.end(),0); for(int i=0;i<n;++i){ parent[i]=i; } } int Find(int idx){ if(parent[idx]==idx){ return idx; } //更新父亲 parent[idx]=Find(parent[idx]); return parent[idx]; } //合并 void Union(int idx1, int idx2){ int newroot=Find(idx2); parent[Find(idx1)]=newroot; } //判断是否连通 bool isConnect(int idx1,int idx2){ int par1=Find(idx1); int par2=Find(idx2); if(par1==par2){ return true; }else{ return false; } } }; class Solution { public: int FindLen(vector<int> &point1,vector<int> &point2){ return abs(point1[0]-point2[0])+abs(point1[1]-point2[1]); } int minCostConnectPoints(vector<vector<int>>& points) { int n=points.size(); UnionFind uf(n); vector<Edge> path; for(int i=0;i<n;++i){ for(int j=i+1;j<n;++j){ int len=FindLen(points[i], points[j]); Edge temp(i,j,len); path.emplace_back(temp); } } //排序,注意慎重加=号,否则等于会堆栈溢出报错 sort(path.begin(),path.end(),[](Edge &x, Edge &y)->bool{ return x.cost<y.cost; }); //总边数 int count_edge=0; int ret=0; for(int i=0;i<path.size();++i){ auto tempEdeg=path[i]; int idx1=tempEdeg.start; int idx2=tempEdeg.end; if(uf.isConnect(idx1, idx2)){ continue; }else{ uf.Union(idx1, idx2); ret+=tempEdeg.cost; ++count_edge; } if(count_edge==(n-1)){ return ret; } } return ret; } };
Prim算法
基本理论
-
「Prim 算法」是求解「加权无向图」的「最小生成树」的另一种算法。——普里姆算法。
-
步骤描述:从单一顶点开始,普里姆算法按照以下步骤逐步扩大树中所含顶点的数目,直到遍及连通图的所有顶点。
- 1.输入:一个加权连通图,其中顶点集合为V,边集合为E:
- 2.初始化:$V_{new}$,其中 x 为集合 V 中的任一节点(起始点),$E_{new}$= { }:
- 3.重复下列操作,直到$V_{new}$=V:
- 3.1 在集合 E 中选取权值最小的边
(u,v),其中u为集合$V_{new}$中的元素,而v则是 V 中没有加入$V_{new}$的顶点(如果存在有多条满足前述条件即具有相同权值的边,则可任意选取其中之一); - 3.2 将
v加入集合$V_{new}$中,将(u,v)加入集合$E_{new}$中;
- 3.1 在集合 E 中选取权值最小的边
- 4.输出:使用集合$V_{new}$和$E_{new}$来描述所得到的最小生成树。
-
所以关键点:定义两个顶点数组
visited[]和no_visited[]。 -
Kruskal 算法和 Prim 算法的区别
在「Kruskal 算法」中,我们通过增加边数来扩大「最小生成树」;
在「Prim 算法」中,我们通过增加顶点来扩大「最小生成树」。
-
时间复杂度:
- 普通二叉堆:$O(ElogV)$。
- 斐波那契堆:$O(E+VlogV)$,V表示顶点数,E表示边数。
-
空间复杂度:$O(V)$ ,V表示顶点数。
示例
-
给你一个
points数组,表示 2D 平面上的一些点,其中points[i] = [xi, yi]。连接点
[xi, yi]和点[xj, yj]的费用为它们之间的 曼哈顿距离 :|xi - xj| + |yi - yj|,其中|val|表示val的绝对值。请你返回将所有点连接的最小总费用。只有任意两点之间 有且仅有 一条简单路径时,才认为所有点都已连接。
-
思路:
- 设置
vector<bool> visited(n,false);判断顶点状态 - 添加
Edge类 - 使用
priority_queue优先队列判断进行最小值输出,作为小顶堆。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65class Edge{ public: int start; int end; int cost; Edge(int start1,int end1, int cost1):start(start1),end(end1),cost(cost1){} }; //这是小顶堆的判断结构体 struct cmp { bool operator()(const Edge& f1, const Edge& f2) { return f1.cost>f2.cost; } }; class Solution { public: int cal_cost(vector<vector<int>>& points,int idx1, int idx2){ return abs(points[idx1][0]-points[idx2][0])+abs(points[idx1][1]-points[idx2][1]); } int minCostConnectPoints(vector<vector<int>>& points) { int n=points.size(); vector<bool> visited(n,false); //小顶堆的优先队列 priority_queue<Edge,vector<Edge>,cmp> pq; visited[0]=true; int count=1; int ret=0; //先加入第0个点的所有边 for(int i=0;i<n;++i){ if(!visited[i]){ int cost=cal_cost(points, 0, i); Edge temp(0,i,cost); pq.push(temp); } } while(!pq.empty()&&count<n){ //确认下一顶点没访问过 Edge tempEdge=pq.top(); pq.pop(); int idx=tempEdge.end; while(visited[idx]){ tempEdge=pq.top(); pq.pop(); idx=tempEdge.end; } //添加,修改节点状态 ret+=tempEdge.cost; visited[idx]=true; ++count; //继续加入没访问的节点 for(int i=0;i<n;++i){ if(!visited[i]){ int cost1=cal_cost(points, idx, i); Edge temp(idx,i,cost1); pq.push(temp); } } } return ret; } }; - 设置
单源最短路径算法
先验知识
-
说到「最短路径」,在前面我们也接触过。我们用「广度优先遍历」算法高效的解决了给定两个顶点之间的「最短路径」。但「广度优先遍历」算法只能解决「无权图」的「最短路径」问题。但现实生活中,我们往往将「最短路径」应用在「加权图」。
-
最短路径问题是图论研究中的一个经典算法问题,旨在寻找图(由结点和路径组成的)中两结点之间的最短路径。算法具体的形式包括:
- 确定起点的最短路径问题 - 也叫单源最短路问题,即已知起始结点,求最短路径的问题。在边权非负时适合使用Dijkstra算法,若边权为负时则适合使用Bellman-ford算法或者SPFA算法。
- 确定终点的最短路径问题 - 与确定起点的问题相反,该问题是已知终结结点,求最短路径的问题。在无向图中该问题与确定起点的问题完全等同,在有向图中该问题等同于把所有路径方向反转的确定起点的问题。
- 确定起点终点的最短路径问题 - 即已知起点和终点,求两结点之间的最短路径。
- 全局最短路径问题 - 也叫多源最短路问题,求图中所有的最短路径。适合使用Floyd-Warshall算法。
-
用于解决最短路径问题的算法被称做“最短路径算法”,有时被简称作“路径算法”。最常用的路径算法有:
- Dijkstra算法
- 0-1广度优先搜索
- A*算法
- Bellman-Ford算法
- SPFA算法(Bellman-Ford算法的改进版本)
- Floyd-Warshall算法
- Johnson最短路算法
- 双向搜索
-
这里学习两个基本的「单源最短路径」的算法:
- Dijkstra 算法;迪杰斯特拉
- Bellman-Ford 算法。贝尔曼-福特
「Dijkstra 算法」只能解决加权有向图的权重为非负数的「单源最短路径」问题。
「Bellman-Ford 算法」能解决加权有向图中包含权重为负数的「单源最短路径」问题。
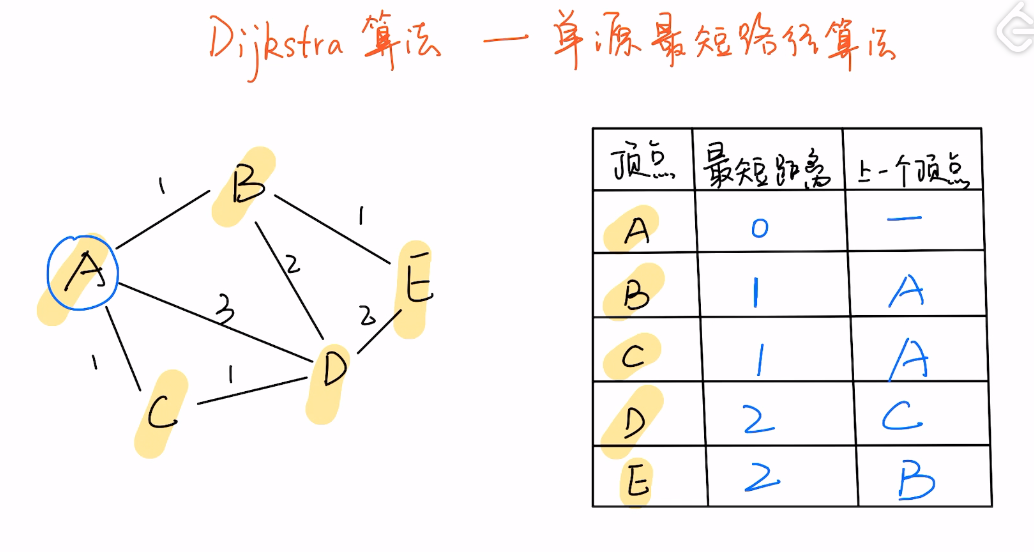
Dijkstra 算法
基本理论
-
朴素版本的Dijkstra算法实现比较简单,优先队列的写法的注意点也只是重载运算符和比较器的写法的注意点。
-
朴素版本
-
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21struct edge { int v, w; }; vector<edge> e[maxn]; int dis[maxn], vis[maxn]; void dijkstra(int n, int s) { memset(dis, 63, sizeof(dis)); dis[s] = 0; for (int i = 1; i <= n; i++) { int u = 0, mind = 0x3f3f3f3f; for (int j = 1; j <= n; j++) if (!vis[j] && dis[j] < mind) u = j, mind = dis[j]; vis[u] = true; for (auto ed : e[u]) { int v = ed.v, w = ed.w; if (dis[v] > dis[u] + w) dis[v] = dis[u] + w; } } } -
优先队列实现
-
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32struct edge { int v, w; }; struct node { int dis, u; bool operator>(const node& a) const { return dis > a.dis; } }; vector<edge> e[maxn]; int dis[maxn], vis[maxn]; priority_queue<node, vector<node>, greater<node> > q; void dijkstra(int n, int s) { memset(dis, 63, sizeof(dis)); dis[s] = 0; q.push({0, s}); while (!q.empty()) { int u = q.top().u; q.pop(); if (vis[u]) continue; vis[u] = 1; for (auto ed : e[u]) { int v = ed.v, w = ed.w; if (dis[v] > dis[u] + w) { dis[v] = dis[u] + w; q.push({dis[v], v}); } } } } -

-
松弛操作是算法的基础,类似两个绳子,一根松一根紧,我们就取紧。
-
算法证明:类似贪心,同时因为是非负权图,所以每一步的最短一定是当前最短,然后再进行松弛操作更新其他最短。最终得出的就是最短的路径。
-
关键:维护两个顶点集合S和Q;松弛操作。
-
「Dijkstra 算法」针对的「图」的类型 必须 满足以下条件:
所有边的权重为非负数。
-
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23//伪代码 //G为带有顶点a=v0,v1,v2...和若干边w(vi,vj) procedure Dijkstra(G:边全为正权的图){ //初始化所有顶点的距离,0和无穷大 for i=1 to n D(vi)=无穷; D(v0)=0;//v0为起始点 S=空集; Q=所有顶点集合; //更新最短路径 while S!=Q(就是循环n次){ u = 不属于S的D(u)最小的顶点;//这里可以使用优先队列、二叉堆进行优化 S += u; //进行松弛操作 for 所有不属于S的顶点v && w(u,v)存在{ if(D(u)+w(u,v)< D(v)){ D(v)=D(u)+w(u,v); } } } //最后的集合D即为所有顶点的最短路径; } -
-
时间复杂度
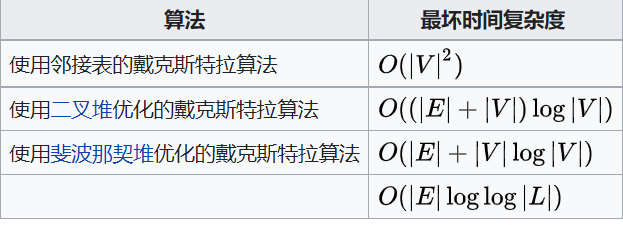
-
空间复杂度:$O(V)$ ,V表示顶点数。
示例
-
有
n个网络节点,标记为1到n。给你一个列表
times,表示信号经过 有向 边的传递时间。times[i] = (ui, vi, wi),其中ui是源节点,vi是目标节点,wi是一个信号从源节点传递到目标节点的时间。现在,从某个节点
K发出一个信号。需要多久才能使所有节点都收到信号?如果不能使所有节点收到信号,返回-1。- 思路:直接Dijkstra算法,组成邻接矩阵,注意下标
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48class Solution { public: int networkDelayTime(vector<vector<int>>& times, int n, int k) { const int inf= INT_MAX;//无穷大 //组成邻接矩阵, 方向从行指向列 vector<vector<int>> graph(n,vector<int>(n,inf)); for(auto &i:times){ graph[i[0]-1][i[1]-1]=i[2]; } //初始化距离 vector<int> Distance(n,inf); //给起点赋初值距离 Distance[k-1]=0; //顶点是否访问数组 vector<bool> used(n,false); //循环n次就够了 for(int i=0;i<n;++i){ //找距离最短同时没使用的点,直接穷举,可以小顶堆优化,优先队列 int x=-1; for(int y=0;y<n;++y){ if(!used[y]){ if(x==-1){ x=y; }else if(Distance[y]<Distance[x]){ x=y; } } } used[x]=true; //松弛操作 for(int y=0;y<n;++y){ if(graph[x][y]==inf||Distance[x]==inf){ continue; }else{ Distance[y]=min(Distance[y],Distance[x]+graph[x][y]); } } } int ret=*max_element(Distance.begin(),Distance.end()); return ret==inf?-1:ret; } }; -
给你一个 m x n 的网格图
grid。grid中每个格子都有一个数字,对应着从该格子出发下一步走的方向。grid[i][j]中的数字可能为以下几种情况:- 1 ,下一步往右走,也就是你会从
grid[i][j]走到grid[i][j + 1] - 2 ,下一步往左走,也就是你会从
grid[i][j]走到grid[i][j - 1] - 3 ,下一步往下走,也就是你会从
grid[i][j]走到grid[i + 1][j] - 4 ,下一步往上走,也就是你会从
grid[i][j]走到grid[i - 1][j]
注意网格图中可能会有 无效数字 ,因为它们可能指向
grid以外的区域。一开始,你会从最左上角的格子
(0,0)出发。我们定义一条 有效路径 为从格子(0,0)出发,每一步都顺着数字对应方向走,最终在最右下角的格子(m - 1, n - 1)结束的路径。有效路径 不需要是最短路径 。你可以花费
cost = 1的代价修改一个格子中的数字,但每个格子中的数字 只能修改一次 。请你返回让网格图至少有一条有效路径的最小代价。
- 思路:构建成每个顶点都有四条边的有向无环图,因为没有负权边,可以使用迪杰特斯拉算法。

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55class Solution { public: const int inf=INT_MAX; const int dirs[4][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}}; struct cmp{ bool operator()(pair<int,int> &a,pair<int,int> &b){ return a.second>b.second; } }; int minCost(vector<vector<int>>& grid) { int m=grid.size(); int n=grid[0].size(); vector<int> Distance(m*n,inf); vector<bool> visited(m*n,false); Distance[0]=0; //小顶堆,pair<int,int>,一个坐标,一个距离 priority_queue<pair<int,int>,vector<pair<int,int>>,cmp> Vetex; Vetex.emplace(0,0); while(!Vetex.empty()){ auto temp_vectex=Vetex.top(); Vetex.pop(); //判断是否查过这个点 if(visited[temp_vectex.first]){ continue; } //已经找到了最短的顶点 int curPoint=temp_vectex.first; int disCurr=temp_vectex.second; visited[curPoint]=true; int row=curPoint/n;//行 int col=curPoint%n;//列 //只有四条边 for(int i=0;i<4;++i){ int newrow=row+dirs[i][0]; int newcol=col+dirs[i][1]; //编程技巧 int newDist=Distance[curPoint]+(grid[row][col]!=(i+1)); if(newrow>=0&&newrow<m&&newcol>=0&&newcol<n){ int newPoint=newrow*n+newcol; //查找没找过的最小顶点,不加也没什么关系 if(visited[newPoint]){ continue; } if(newDist<Distance[newPoint]){ Distance[newPoint]=newDist; Vetex.emplace(newPoint,newDist); } } } } return Distance.back(); } }; - 1 ,下一步往右走,也就是你会从
-
-
这道题很难,看看思路就行
-
思路1:朴素版Dijkstra算法+二分查找
-

-
为什么是K*(D-1)+1,每次递增1,保证D的个数逐渐增加,最后全为D。
-
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98class Solution { public: vector<vector<int>> modifiedGraphEdges(int n, vector<vector<int>> &edges, int source, int destination, int target) { int k = 0; for (const auto &e : edges) { if (e[2] == -1) { ++k; } } if (dijkstra(source, destination, construct(n, edges, 0, target)) > target) { return {}; } if (dijkstra(source, destination, construct(n, edges, static_cast<long long>(k) * (target - 1), target)) < target) { return {}; } long long left = 0, right = static_cast<long long>(k) * (target - 1), ans = 0; while (left <= right) { long long mid = (left + right) / 2; if (dijkstra(source, destination, construct(n, edges, mid, target)) >= target) { ans = mid; right = mid - 1; } else { left = mid + 1; } } for (auto &e : edges) { if (e[2] == -1) { if (ans >= target - 1) { e[2] = target; ans -= (target - 1); } else { e[2] = 1 + ans; ans = 0; } } } return edges; } long long dijkstra(int source, int destination, const vector<vector<int>> &adj_matrix) { // 朴素的 dijkstra 算法 // adj_matrix 是一个邻接矩阵 int n = adj_matrix.size(); vector<long long> dist(n, INT_MAX / 2); vector<int> used(n); dist[source] = 0; for (int round = 0; round < n - 1; ++round) { int u = -1; for (int i = 0; i < n; ++i) { if (!used[i] && (u == -1 || dist[i] < dist[u])) { u = i; } } used[u] = true; for (int v = 0; v < n; ++v) { if (!used[v] && adj_matrix[u][v] != -1) { dist[v] = min(dist[v], dist[u] + adj_matrix[u][v]); } } } return dist[destination]; } vector<vector<int>> construct(int n, const vector<vector<int>> &edges, long long idx, int target) { // 需要构造出第 idx 种不同的边权情况,返回一个邻接矩阵 vector<vector<int>> adj_matrix(n, vector<int>(n, -1)); for (const auto &e : edges) { int u = e[0], v = e[1], w = e[2]; if (w != -1) { adj_matrix[u][v] = adj_matrix[v][u] = w; } else { if (idx >= target - 1) { adj_matrix[u][v] = adj_matrix[v][u] = target; idx -= (target - 1); } else { adj_matrix[u][v] = adj_matrix[v][u] = 1 + idx; idx = 0; } } } return adj_matrix; } };
-
-
思路2:两次Dijkstra算法
-
思维难度很大
-

-
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68class Solution { public: vector<vector<int>> modifiedGraphEdges(int n, vector<vector<int>> &edges, int source, int destination, int target) { this->target = target; vector<vector<int>> adj_matrix(n, vector<int>(n, -1)); // 邻接矩阵中存储边的下标 for (int i = 0; i < edges.size(); ++i) { int u = edges[i][0], v = edges[i][1]; adj_matrix[u][v] = adj_matrix[v][u] = i; } from_destination = dijkstra(0, destination, edges, adj_matrix); if (from_destination[source] > target) { return {}; } vector<long long> from_source = dijkstra(1, source, edges, adj_matrix); if (from_source[destination] != target) { return {}; } return edges; } vector<long long> dijkstra(int op, int source, vector<vector<int>> &edges, const vector<vector<int>> &adj_matrix) { // 朴素的 dijkstra 算法 // adj_matrix 是一个邻接矩阵 int n = adj_matrix.size(); vector<long long> dist(n, INT_MAX / 2); vector<int> used(n); dist[source] = 0; for (int round = 0; round < n - 1; ++round) { int u = -1; for (int i = 0; i < n; ++i) { if (!used[i] && (u == -1 || dist[i] < dist[u])) { u = i; } } used[u] = true; for (int v = 0; v < n; ++v) { if (!used[v] && adj_matrix[u][v] != -1) { if (edges[adj_matrix[u][v]][2] != -1) { dist[v] = min(dist[v], dist[u] + edges[adj_matrix[u][v]][2]); } else { if (op == 0) { dist[v] = min(dist[v], dist[u] + 1); } else { int modify = target - dist[u] - from_destination[v]; if (modify > 0) { dist[v] = min(dist[v], dist[u] + modify); edges[adj_matrix[u][v]][2] = modify; } else { edges[adj_matrix[u][v]][2] = target; } } } } } } return dist; } private: vector<long long> from_destination; int target; };
Bellman-Ford 算法
基本理论
-
定理一:在一个有 N 个顶点的「非负权环图」中,两点之间的最短路径最多经过 N-1 条边。(没有负权环,允许有负权边。
-
定理二:在一个有 N 个顶点的「负权环图」中,不存在最短路径。
-
贝尔曼福特算法基于以上两个定理,原理是对图进行$|v|-1$次松弛操作,得到所有可能的最短路径。其优于迪杰斯特拉算法的方面是边的权值可以为负数、实现简单,缺点是时间复杂度过高,高达$O(|V|*|E|)$。但算法可以进行若干种优化,从而提高效率。
-
就像Dijkstra算法一样,我们需要定义
distance数组表示每个顶点到起始点的最短距离。不同的是,我们需要所有边都要计算,计算N-1次。 -
这个算法已经不属于贪心思路,而是动态规划。
-

-
伪代码
注意下面的伪代码已经是动态规划优化过了的,已经把两个一维数组变成一个一维滚动数组了。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23procedure BellmanFord(list vertices, list edges, vertex source){ // 该函数读入边和节点的列表,并向两个数组(distance和predecessor)中写入最短路径信息 // 步骤1:初始化图 for each vertex v in vertices: if v is source then distance[v] := 0 else distance[v] := infinity predecessor[v] := null // 步骤2:重复对每一条边进行松弛操作,N-1次,包括最后的size(vertices)-1 for i from 1 to size(vertices)-1: for each edge (u, v) with weight w in edges: if distance[u] + w < distance[v]: distance[v] := distance[u] + w predecessor[v] := u // 步骤3:检查负权环 for each edge (u, v) with weight w in edges: if distance[u] + w < distance[v]: error "图包含了负权环" //最终的distance[]数组就是最短路径,predecessor[]数组是前一个节点,可以不要 } -
优化:在实际操作中,贝尔曼-福特算法经常会在未达到$|v|-1$次前就得出解,$|v|-1$其实是最大值。于是可以在循环中设置判定,在某次循环不再进行松弛时,直接退出循环,进行负权环判定。从而可以计算最多经过k条边的最短距离问题。
-
Bellman-Ford 算法」针对的「图」的类型必须满足以下条件:
「图」中不能包含「负权环」。
-
时间复杂度:$O(|V|*|E|)$
-
空间复杂度:$O(V)$ ,V表示顶点数。
示例
-
有
n个城市通过一些航班连接。给你一个数组flights,其中flights[i] = [fromi, toi, pricei],表示该航班都从城市fromi开始,以价格pricei抵达toi。现在给定所有的城市和航班,以及出发城市
src和目的地dst,你的任务是找到出一条最多经过k站中转的路线,使得从src到dst的 价格最便宜 ,并返回该价格。 如果不存在这样的路线,则输出-1。- 思路,最短k站中转,明显只能是原始的Bellman-Ford算法才能胜任
- 这次两个一维滚动数组不能合并,所以需要有先后
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36class Solution { public: int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int k) { //初始化距离 const int inf=INT_MAX; vector<int> Distance(n,inf); vector<int> Predecessor(n,inf); Distance[src]=0;//现在的 Predecessor[src]=0;//上一次的数组 //计算循环次数 int count=k;//[0-k] if(k>n-2){ count=n-2; } for(int j=0;j<=count;++j){ for(auto &i:flights){ int u=i[0]; int v=i[1]; int cost=i[2]; if(Predecessor[u]==inf){ continue; } //注意是小于现在的Distance[v],而不是过去的Predecessor[v] else{ Distance[v]=min(Distance[v],Predecessor[u]+cost); } } //更换新数组 for(int i=0;i<n;++i){ Predecessor[i]=Distance[i]; } } return Distance[dst]==inf?-1:Distance[dst]; } };
SPFA 算法
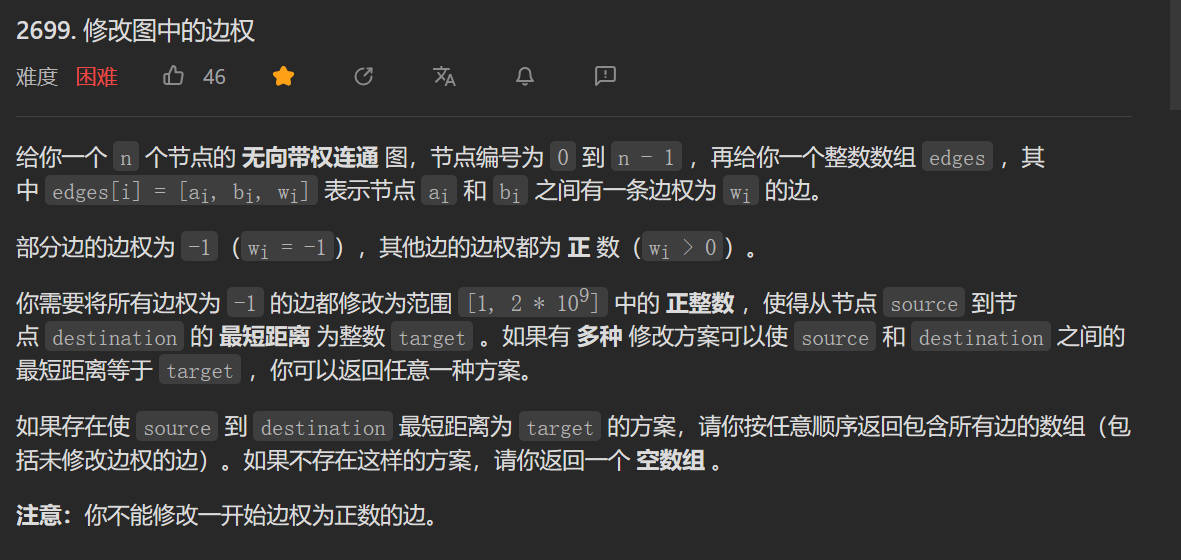
基本理论
-
SPFA 算法是基于「队列」优化的 Bellman-Ford 算法 。(Shortest Path Faster Algorithm)
-
「SPFA 算法」主要是通过「队列」来维护我们接下来要遍历边的起点,而不是「Bellman Ford」算法中的任意还没有遍历过的边。每次只有当某个顶点的最短距离更新之后,并且该顶点不在「队列」中,我们就将该顶点加入到「队列」中。一直循环以上步骤,直到「队列」为空,我们就可以终止算法。此时,我们就可以得到「图」中其他顶点到给定顶点的最短距离了。
-
SPFA算法的改进之处在于它并不盲目地尝试所有节点,而是维护一个备选的节点队列,并且仅有节点被松弛后才会放入队列中。整个流程不断重复直至没有节点可以被松弛。
-
维护一个距离数组
distance[],顶点是否被松弛的标记数组visited[],备选节点队列queue。 -
-
注意:SPFA 不能判断是否有负权环,但可以快速计算顶点之间的最短距离。
-
时间复杂度:$O(|V|*|E|)$
-
空间复杂度:$O(V)$ ,V表示顶点数。
示例
-
给你一个 m x n 的网格图
grid。grid中每个格子都有一个数字,对应着从该格子出发下一步走的方向。grid[i][j]中的数字可能为以下几种情况:- 1 ,下一步往右走,也就是你会从
grid[i][j]走到grid[i][j + 1] - 2 ,下一步往左走,也就是你会从
grid[i][j]走到grid[i][j - 1] - 3 ,下一步往下走,也就是你会从
grid[i][j]走到grid[i + 1][j] - 4 ,下一步往上走,也就是你会从
grid[i][j]走到grid[i - 1][j]
注意网格图中可能会有 无效数字 ,因为它们可能指向
grid以外的区域。一开始,你会从最左上角的格子
(0,0)出发。我们定义一条 有效路径 为从格子(0,0)出发,每一步都顺着数字对应方向走,最终在最右下角的格子(m - 1, n - 1)结束的路径。有效路径 不需要是最短路径 。你可以花费
cost = 1的代价修改一个格子中的数字,但每个格子中的数字 只能修改一次 。请你返回让网格图至少有一条有效路径的最小代价。
- 思路:构建成每个顶点都有四条边的有向无环图,因为没有负权边,可以使用迪杰特斯拉算法。

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48class Solution { public: const int inf=INT_MAX; const int dirs[4][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}}; int minCost(vector<vector<int>>& grid) { //初始化 int m=grid.size(); int n=grid[0].size(); vector<int> Distance(m*n,inf); vector<bool> visited(m*n,false); Distance[0]=0; queue<int> Vetex; Vetex.emplace(0); visited[0]=true; //循环队列 while(!Vetex.empty()){ auto temp_vectex=Vetex.front(); Vetex.pop(); int curPoint=temp_vectex; //弹出就把标记删除 visited[curPoint]=false; int disCurr=Distance[curPoint]; int row=curPoint/n;//行 int col=curPoint%n;//列 //只有四条边 for(int i=0;i<4;++i){ int newrow=row+dirs[i][0]; int newcol=col+dirs[i][1]; //编程技巧 int newDist=Distance[curPoint]+(grid[row][col]!=(i+1)); if(newrow>=0&&newrow<m&&newcol>=0&&newcol<n){ int newPoint=newrow*n+newcol; if(newDist<Distance[newPoint]){ Distance[newPoint]=newDist; //没添加进队列的顶点才做标记,同时添加进队列 if(!visited[newPoint]){ visited[newPoint]=true; Vetex.emplace(newPoint); } } } } } return Distance.back(); } }; - 1 ,下一步往右走,也就是你会从
0-1 BFS
基本理论
-
常规的广度优先搜索可以找出在边权均为 1 时的单源最短路,然而在常规的建模中,边权除了 1 之外也可能为 0。我们是否可以修改广度优先搜索的算法框架,使得它可以找出在边权为 0 或 1 时的单源最短路呢?
-
保证广度优先搜索正确性的基础在于:对于源点 s 以及任意两个节点 u 和 v,如果 $dist(s,u)<dist(s,v)$ ,那么节点 u 一定会比节点 v 先被取出队列。在常规的广度优先搜索中,我们使用队列作为维护节点的数据结构,就保证了从队列中取出的节点,它们与源点之间的距离是单调递增的。
-
但是当边权可以为0时,队列这个数据结构已经无法满足上述单调性了。
-
我们可以使用双端队列(double-ended queue, deque)代替普通的队列作为维护节点的数据结构。当任一节点 u 被取出队列时,如果它到某节点 $v_i$ 有一条权值为 0 的边,那么就将节点 $v_i$ 加入双端队列的「队首」。如果它到某节点 $v_j$ 有一条权值为 1 的边,那么和常规的广度优先搜索相同,我们将节点 $v_j$ 加入双端队列的「队尾」。这样以来,我们保证了任意时刻从队首到队尾的所有节点,它们与源点之间的距离是单调递增的,即从队列中取出的节点与源点之间的距离同样是单调递增的。
-
0-1广度优先搜索的实现其实与 Dijkstra 算法非常相似。在Dijkstra算法中,我们用优先队列保证了距离的单调递增性。而在0-1广度优先搜索中,实际上任意时刻队列中的节点与源点的距离均为d或d+1(其中d为某一非负整数),并且所有与源点距离为d的节点都出现在队首附近,所有与源点距离为d+1的节点都出现在队尾附近。因此,我们只要使用双端队列,对于边权为0和1的两种情况分别将对应节点添加至队首和队尾,就保证了距离的单调递增性。
-
伪代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17//初始化 for all v in vertices: dist[v] = inf dist[source] = 0; //计算距离 deque d d.push_front(source) while d.empty() == false: vertex = get front element and pop as in BFS. //vertex是起点,u是终点 for all edges e of form (vertex , u): if travelling e relaxes distance to u: relax dist[u] if e.weight = 1: d.push_back(u) else: d.push_front(u)
示例
-
给你一个 m x n 的网格图
grid。grid中每个格子都有一个数字,对应着从该格子出发下一步走的方向。grid[i][j]中的数字可能为以下几种情况:- 1 ,下一步往右走,也就是你会从
grid[i][j]走到grid[i][j + 1] - 2 ,下一步往左走,也就是你会从
grid[i][j]走到grid[i][j - 1] - 3 ,下一步往下走,也就是你会从
grid[i][j]走到grid[i + 1][j] - 4 ,下一步往上走,也就是你会从
grid[i][j]走到grid[i - 1][j]
注意网格图中可能会有 无效数字 ,因为它们可能指向
grid以外的区域。一开始,你会从最左上角的格子
(0,0)出发。我们定义一条 有效路径 为从格子(0,0)出发,每一步都顺着数字对应方向走,最终在最右下角的格子(m - 1, n - 1)结束的路径。有效路径 不需要是最短路径 。你可以花费
cost = 1的代价修改一个格子中的数字,但每个格子中的数字 只能修改一次 。请你返回让网格图至少有一条有效路径的最小代价。
- 思路:构建成每个顶点都有四条边的有向无环图,因为没有负权边,可以使用迪杰特斯拉算法。

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55class Solution { public: const int inf=INT_MAX; const int dirs[4][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}}; int minCost(vector<vector<int>>& grid) { int m=grid.size(); int n=grid[0].size(); vector<int> Distance(m*n,inf); vector<bool> visited(m*n,false); Distance[0]=0; deque<int> Vetex; Vetex.push_back(0); while(!Vetex.empty()){ //BFS操作 auto temp_vectex=Vetex.front(); Vetex.pop_front(); if(visited[temp_vectex]){ continue; } int curPoint=temp_vectex; visited[curPoint]=true; int disCurr=Distance[curPoint]; int row=curPoint/n;//行 int col=curPoint%n;//列 //只有四条边 for(int i=0;i<4;++i){ int newrow=row+dirs[i][0]; int newcol=col+dirs[i][1]; //编程技巧 int newDist=Distance[curPoint]+(grid[row][col]!=(i+1)); if(newrow>=0&&newrow<m&&newcol>=0&&newcol<n){ int newPoint=newrow*n+newcol; //类似Dijkstra,取最短的边了,不加也没关系 if(visited[newPoint]){ continue; } if(newDist<Distance[newPoint]){ Distance[newPoint]=newDist; //根据权重加入双端队列 if(grid[row][col]==(i+1)){ Vetex.push_front(newPoint); }else{ Vetex.push_back(newPoint); } } } } } return Distance.back(); } }; - 1 ,下一步往右走,也就是你会从
多源最短路径算法
- 其实对单源最短路径进行多次循环,也可以得到和多源最短路径算法一样的结果。
Floyd-Warshall算法
-
Floyd算法也用于解决最短路径问题,与其他算法不同的是它可以解决的是多源最短路径问题,即不固定起点和终点,求出任意两点间的最短距离。该算法的时间复杂度为 $O(n^3)$ 。
-
这个算法的最大优势在于它可以一次性求出任意两点间的最短距离。但由于过高的时间复杂度,所以不经常被使用。用Dijkstra或Bellman-Ford算法执行多次也可以达到此效果。
-
Floyd-Warshall算法的基本思想是通过迭代更新每对节点之间的最短路径长度。它使用一个二维数组来存储任意两个节点之间的最短路径长度,并通过不断更新这个数组来得到最终的结果。
-
在处理负权图时,Floyd-Warshall算法可以正确地找到最短路径。它通过在每个迭代步骤中考虑所有中间节点,逐渐更新路径长度,直到找到所有节点对之间的最短路径。然而,如果图中存在负权环(即环的权重之和为负),那么Floyd-Warshall算法将无法得到正确的结果,因为不存在最短路径。
-
基本思想就是动态规划。
-
采用邻接矩阵,三重for循环,枚举所有连接的点,不连接设为无穷大即可,同一个点设为0。
-
1 2 3 4 5 6 7 8 9 10int mp[n][n]; void floyd() { for (int k = 0; k < n; k++) { for (int i = 0; i < n; i++) { for (int j = 0; j < n; j++) { mp[i][j] = min(mp[i][j], mp[i][k] + mp[k][j]); } } } } -
知道注意这个Floyd算法和Floyd判环法的区别,虽然名字都一样。
拓扑排序之 Kahn 算法
先验知识
-
上大学的时候,有些高级的课程需要你先完成基础课程后才可以学习。在下面的课程关系图中,如果你想选课程 C,那你需要先完成课程 B,如果你想选课程 B,那么你需要先完成课程 A。大学四年的课程还是非常多的,你总不希望等到大四了,想去修一门高级的课程,结果发现自己并没有完成基础课程,最终导致自己无法学习这门高级课程。那么你应当如何合理的安排自己的课程呢?如何才能理清课程关系呢?这就需要
拓扑排序的帮忙了。课程关系图 
-
拓扑排序」针对的是 有向无环图 的一种算法。它是对「图」中所有顶点按照先后顺序的一种线性排序。换句话说,如果存在顶点 u 和顶点 v,要想到达顶点 v,则必须要到达顶点 u ;那么在「拓扑排序」中,顶点 u 必须处于顶点 v 的前面。「拓扑排序」中最有名的算法 Kahn 算法。
-
有向无环图才有拓扑排序,主要应用在具有依赖关系、因果关系的图论问题中,作为预处理的手段之一。
Kahn(卡恩)算法
-
算法针对的图需要满足的两个条件:
- 有向无环图;
- 「图」中至少有一个顶点「入度」为 0 。如果「图」中所有顶点都有「入度」,则代表所有顶点都至少有一个前置顶点,那么这个就没有顶点可以作为「拓扑排序」的起点。
-
步骤描述:
- 1.计算所有不在队列
s的顶点的入度,把入度为0的顶点放入队列S。 - 2.取出队列
S的第一个元素顶点u,放入输出的数组L,找到以u为起点的所有边,将这些边的终点的入度减1。 - 3.重复计算步骤1和步骤2,直到队列
S为空。 - 4.如果此时
L中的元素个数和节点总数相同,说明排序完成;如果L中的元素个数和节点总数不同,说明原图中存在环,无法进行拓扑排序。
- 1.计算所有不在队列
-
伪代码
1 2 3 4 5 6 7 8 9 10 11 12 13L ← 包含已排序的元素的列表,目前为空 S ← 入度为零的节点的集合 当 S 非空时: 将节点n从S移走 将n加到L尾部 选出任意起点为n的边e = (n,m),移除e,同时对于的m的入度减一。如m入度为0,则将m加入S。 重复循环。 如图中有剩余的边则: return error (图中至少有一个环) 否则: return L (L为图的拓扑排序)
示例
-
现在你总共有
numCourses门课需要选,记为0到numCourses - 1。给你一个数组prerequisites,其中prerequisites[i] = [ai, bi],表示在选修课程ai前 必须 先选修bi。- 例如,想要学习课程
0,你需要先完成课程1,我们用一个匹配来表示:[0,1]。
返回你为了学完所有课程所安排的学习顺序。可能会有多个正确的顺序,你只要返回 任意一种 就可以了。如果不可能完成所有课程,返回 一个空数组
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47class Solution { public: vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) { vector<int> ret; queue<int> zeroVetex;//队列 vector<int> course(numCourses,0);//入度数组 vector<bool> isVisited(numCourses,false);//节点访问标志 //初始化入度 for(auto &i:prerequisites){ course[i[0]]+=1; } //初始化队列 for(int i=0;i<numCourses;++i){ if(course[i]==0){ zeroVetex.push(i); } } while(!zeroVetex.empty()){ int u=zeroVetex.front(); zeroVetex.pop(); ret.push_back(u); isVisited[u]=true;//添加标志访问了 for(auto &i:prerequisites){ int v=i[0]; if(isVisited[v]){ continue; } if(i[1]==u){ course[v]-=1; if(course[v]==0){ zeroVetex.push(v); } } } } for(int i=0;i<numCourses;++i){ if(isVisited[i]==false){ return vector<int>{}; } } // if(ret.size()!=numCourses){ // return vector<int>{}; // } return ret; } }; - 例如,想要学习课程
-
给定一个长度为
n的整数数组nums,其中nums是范围为[1,n]的整数的排列。还提供了一个 2D 整数数组sequences,其中sequences[i]是nums的子序列。 检查nums是否是唯一的最短 超序列 。最短 超序列 是 长度最短 的序列,并且所有序列sequences[i]都是它的子序列。对于给定的数组sequences,可能存在多个有效的 超序列 。- 例如,对于
sequences = [[1,2],[1,3]],有两个最短的 超序列 ,[1,2,3]和[1,3,2]。 - 而对于
sequences = [[1,2],[1,3],[1,2,3]],唯一可能的最短 超序列 是[1,2,3]。[1,2,3,4]是可能的超序列,但不是最短的。
如果
nums是序列的唯一最短 超序列 ,则返回true,否则返回false。 子序列 是一个可以通过从另一个序列中删除一些元素或不删除任何元素,而不改变其余元素的顺序的序列。 - 例如,对于
-
思路:拓扑排序
-
我们把sequences看成是一个有向图,若按照拓扑排序,入度为0的点只有一个,则一定是一个最短的超序列,否则不是。 此题也可以理解为,用sequences能不能转化为一个唯一序列。
-
-
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50class Solution { public: bool sequenceReconstruction(vector<int>& nums, vector<vector<int>>& sequences) { //拓扑排序 int n = nums.size(); //建图 vector<unordered_set<int>> grapg(n+1); vector<int> indegree(n+1,0);//入度 for(vector<int> &i:sequences){ int n = i.size(); if(n==1){ continue; } int pred ; int next ; int k = 1; while(k<n){ pred = i[k-1]; next = i[k]; if(!grapg[pred].count(next)){ indegree[next]++; grapg[pred].emplace(next); } pred = next; ++k; } } //开始拓扑 queue<int> qe; for(int i=1;i<=n;++i){ if(indegree[i]==0){ qe.emplace(i); } } while(!qe.empty()){ if(qe.size()>1){ return false; } int tmp = qe.front(); qe.pop(); for(int i:grapg[tmp]){ indegree[i]--; if(indegree[i]==0){ qe.emplace(i); } } } return true; } };
Tarjan 算法
基本理论
- Tarjan 算法是图论中非常实用 / 常用的算法之一,能解决强连通分量(有向图),双连通分量(无向图),割点和桥(无向图),求最近公共祖先(LCA)(常见二叉树)等问题。
- Tarjan算法 (以发现者Robert Tarjan命名)是一个在图中寻找强连通分量的算法。算法的基本思想为:任选一结点开始进行深度优先搜索dfs(若深度优先搜索结束后仍有未访问的结点,则再从中任选一点再次进行)。搜索过程中已访问的结点不再访问。搜索树的若干子树构成了图的强连通分量。
- 关键步骤是维护两个数组
dfn[]low[]
割点和桥问题
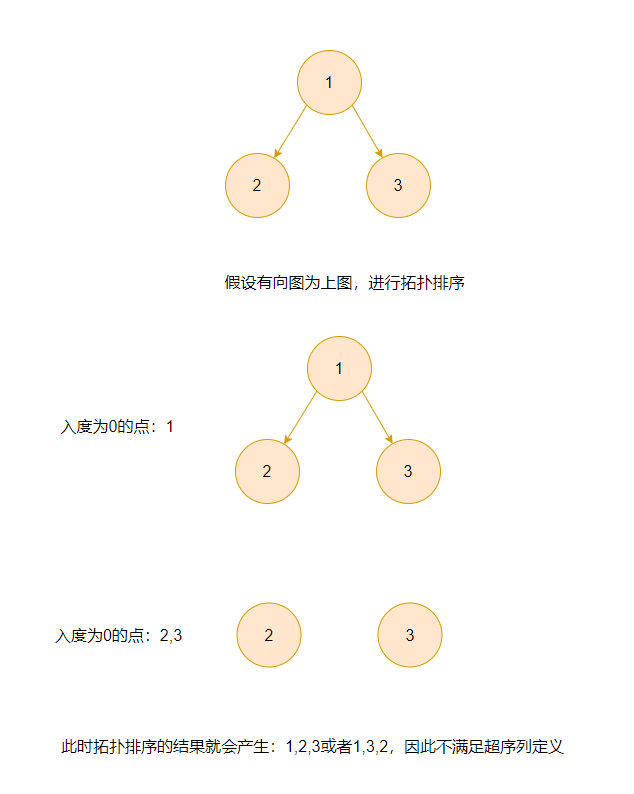
-
针对无向图,连通性是针对顶点。
-
割点:若从图中删除节点 x 以及所有与 x 关联的边之后,图将被分成两个或两个以上的不相连的子图,那么称 x 为图的割点。如下图的1和6。
-
桥:若从图中删除边 e 之后(但是保留顶点,只是把边去了),图将分裂成两个不相连的子图,那么称 e 为图的桥或割边。如下图的Edge(1,6)和Edge(6,7)。
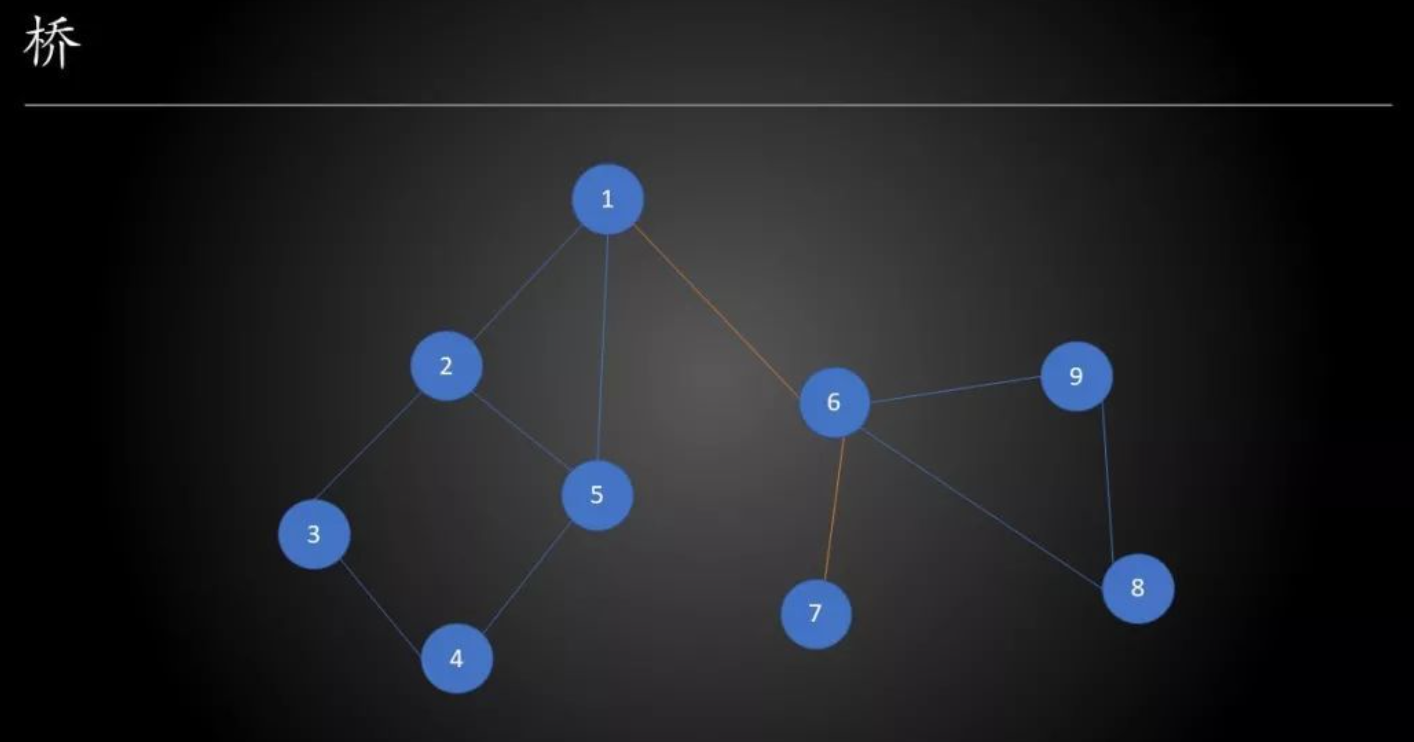
-

-
算法步骤
-
求割边
-
时间戳:时间戳是用来标记图中每个节点在进行深度优先搜索时被访问的时间顺序,当然,你可以理解成一个序号(这个序号由小到大),用
dfn[x]来表示。 -
追溯值:追溯值用来表示从当前节点 x 作为搜索树的根节点出发,能够访问到的所有节点中,时间戳最小的值 ,用
low[x]表示。 -
在无向图中,我们以某一个节点 x 出发进行深度优先搜索,每一个节点只访问一次,所有被访问过的节点与边构成一棵树,我们可以称之为“无向连通图的搜索树”。
-
在一张无向图中,判断边 e (其对应的两个节点分别为 u 与 v)是否为桥,需要其满足如下条件即可:dfn[u] < low[v]。(u->v,在搜索树里面)
-
注意以下模板只针对无向图。有向图会出错,因为不是父亲的已经访问的节点不一定是祖宗节点,有可能无法到达。
-
代码模板
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27//u是当前节点,fathe是父亲节点,无向图当成有向图访问 void tarjan(int u,int father){ //开始遍历初始化 dfn[u]=low[u]=++num; //遍历子节点 for(int v:graph[u]){ //父亲节点不访问 if(v==father){ continue; } //没访问过继续访问 if(!dfn[v]){ //横向搜索子树 tarjan(v, u); //计算u的追溯值,因为子树可能会成环从而更新low low[u] = min(low[u], low[v]); //判断桥 if(dfn[u]<low[v]){ ret.emplace_back(vector<int>{u,v}); } } //已经访问过还不是父亲,说明是祖宗,更新追溯值 else{ low[u]=min(low[u],dfn[v]); } } }
示例
-
力扣数据中心有
n台服务器,分别按从0到n-1的方式进行了编号。它们之间以「服务器到服务器」点对点的形式相互连接组成了一个内部集群,其中连接connections是无向的。从形式上讲,connections[i] = [a, b]表示服务器a和b之间形成连接。任何服务器都可以直接或者间接地通过网络到达任何其他服务器。「关键连接」 是在该集群中的重要连接,也就是说,假如我们将它移除,便会导致某些服务器无法访问其他服务器。
请你以任意顺序返回该集群内的所有 「关键连接」。
-
以n = 4, connections = [[0,1],[1,2],[2,0],[1,3]] 示例:
-
思路:返回桥,使用Tarjan算法,用邻接表比较好理解。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57class Solution { public: int num=0; vector<int> dfn;//时间戳,从1开始,初始化为 vector<int> low;//追溯值, 从1开始,初始化为0 vector<vector<int>> graph;//邻接表 vector<vector<int>> ret; //u是当前节点,fathe是父亲节点,无向图当初有向图访问 void tarjan(int u,int father){ dfn[u]=low[u]=++num; //遍历子节点 for(int v:graph[u]){ //父亲节点不访问 if(v==father){ continue; } //没访问过继续访问 if(!dfn[v]){ //横向搜索子树 tarjan(v, u); //计算u的追溯值,因为子树可能会成环从而更新low low[u] = min(low[u], low[v]); //判断桥 if(dfn[u]<low[v]){ ret.emplace_back(vector<int>{u,v}); } } //已经访问过还不是父亲,说明是祖宗,更新追溯值 else{ low[u]=min(low[u],dfn[v]); } } } public: vector<vector<int>> criticalConnections(int n, vector<vector<int>>& connections) { ret.clear(); graph.resize(n);//初始化容量 dfn.resize(n);//初始化都是0 low.resize(n);//初始化都是0 //建立邻接表 for(auto &i:connections){ graph[i[0]].push_back(i[1]); graph[i[1]].push_back(i[0]); } //遍历所有节点,因为有些是不能一次DFS走完的 for(int u=0;u<n;++u){ if(!dfn[u]){ //初始父亲是1 tarjan(u, -1); } } return ret; } }; -
强连通分量个数SCC
-
在有向图中,如果两个顶点至少存在一条路径(可以相互通达),则称两个顶点强连通(strongly connected)。
-
如果有向图G的每两个顶点都强连通,称G是一个强连通图。
-
非强连通有向图的极大强连通子图,称为强连通分量(strongly connected components)。
-

-
在上图中,{1 , 2 , 3 , 4 } , { 5 } , { 6 } 三个区域可以相互连通,称为这个图的强连通分量。
Tarjan算法是基于对图深度优先搜索的算法,每个强连通分量为搜索树中的一棵子树。
dfn[i]: 在DFS中该节点i被搜索的次序(时间戳)。low[i]: 为i或i的子树能够追溯到的最早的栈中节点的次序号。当
dfn[i]==low[i]时,已i为根的搜索子树上所有节点是一个强连通分量。 -
算法伪代码
-
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16tarjan(u) { DFN[u]=Low[u]=++Index // 为节点u设定次序编号和Low初值 Stack.push(u) // 将节点u压入栈中 for each (u, v) in E // 枚举每一条边 if (v is not visted) // 如果节点v未被访问过 tarjan(v) // 继续向下找 Low[u] = min(Low[u], Low[v]) else if (v in S) // 如果节点v还在栈内 Low[u] = min(Low[u], DFN[v]) if (DFN[u] == Low[u]) // 如果节点u是强连通分量的根 do v = S.pop // 将v退栈,为该强连通分量中一个顶点 print v while (u== v) } -
示例程序如下,但是判断节点是否在栈中,采用一个bool类型的数组判断
-
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110#include <iostream> #include <vector> #include <stack> using namespace std; int num = 0; vector<int> dfn;//时间戳,从1开始,初始化为 vector<int> low;//追溯值, 从1开始,初始化为0 vector<vector<int>> graph;//邻接表 stack<int> Check_huan;//栈,判断环 vector<bool> visited;//判断是否在栈里面 //u是当前节点 void tarjan(int u) { ++num; dfn[u] = num; low[u] = num; //节点入栈 Check_huan.push(u); visited[u] = true; for (int &v:graph[u]) { //如果节点还没访问 if (!dfn[v]) { //横向搜索子树 tarjan(v); //计算u的追溯值,因为子树可能会成环从而更新low low[u] = min( low[u],low[v]); } //节点v还在栈内 else if (visited[v]) { low[u] = min(low[u], dfn[v]); } } //判断连通分量 if (dfn[u] == low[u]) { int now; //取出包括u的环,注意先跑一遍 do { now = Check_huan.top(); cout << now << " "; visited[now] = false; Check_huan.pop(); } while (now != u); cout << endl; } } int main() { int n; cin >> n;//输入图的节点个数 int m; cin >> m;//输入有向边的个数 vector<vector<int>> Link(m); for (int i = 0; i < m; ++i) { int a, b; cin >> a >> b; Link[i].push_back(a); Link[i].push_back(b); } //逻辑处理 num = 0; dfn.resize(n, 0); low.resize(n, 0); visited.resize(n, false); graph.resize(n); //初始化图 for (int i = 0; i < m; ++i) { //注意每个数都减1 graph[Link[i][0] - 1].push_back(Link[i][1] - 1); } //tarjan算法处理 for (int i = 0; i < n; ++i) { if (!dfn[i]) { tarjan(i); } } //计算个数 int count = 0; for (int i = 0; i < n; ++i) { if (dfn[i] == low[i]) { ++count; } } cout << "强连通分量个数为 : " << count << endl; return 0; } /*输入 6 8 1 2 2 4 4 1 1 3 3 4 4 6 5 6 3 5 /*输出 5 4 2 3 1 0 强连通分量个数为 : 3 */
LCA 应用
-
LCA算法核心:tarjan算法,并查集和DFS(离线)。
-
离线算法的定义
-
算法设计策略都是基于在执行算法前输入数据已知的基本假设,也就是说,对于一个离线算法,在开始时就需要知道问题的所有输入数据,而且在解决一个问题后就要立即输出结果,通常将这类具有问题完全信息前提下设计出的算法成为离线算法( off line algorithms)。
-
首先根据LCA的定义,我们可以想到一种最简单的方法来求u,v的LCA:分别从u,v开始向根节点走,当这两个点走到第一个相同的节点时,这个节点就是LCA(u,v)。但是这样求效率不够,求一次的最坏的时间复杂度就是O(N),若是再多来几个询问就会超时。现在介绍一种当询问次数为Q,节点数为N时时间复杂度为O(N+Q)的离线求LCA的算法。
-
性质: 求 B、C 两点间的距离,设 A 点为 B、C 两点的最近公共祖先,D 为任意一点,则有 |BC| = |BD| + |CD| - 2*|AD|。
-
这种算法是基于DFS和并查集来实现的。其中以下的 dist 只是为了求取两个节点的距离而设置的每个节点到根节点的距离 ,直接深度优先搜索都是可以求出来的。
- 设
fa[x]为x的父亲,dist[x]为x节点到根节点的距离。 - 首先从一号根节点(记为u)开始访问他的每一个子节点(记为v),并用根节点与当前访问的子节点的距离更新dist值,即
dist[v]=dist[u]+map[v][u],其中map[v][u]表示v到u的距离, - 然后将当前子节点当做根点用上述同样步骤递归下去,并在递归回溯后将其fa[v]值更新,这样的目的是保证子节点v的所有子树全部被访问过。
- 设
-
Tarjan 算法基本思路(关键):
1.任选一个点为根节点,从根节点开始。
2.遍历该点 u 所有子节点 v,并标记这些子节点 v 已被访问过。
3.若是 v 还有子节点,返回 2 继续遍历,否则下一步。
4.合并 v 到 u 上。
5.寻找与当前点 u 有询问关系的点 v。
6.若是 v 已经被访问过了,则可以确认 u 和 v 的最近公共祖先为—— v 被合并到的祖先节点 a。
遍历的话需要用到dfs来遍历,至于合并,最优化的方式就是利用并查集来合并两个节点。
-
伪代码
-
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17Tarjan(u)//union和find为并查集合并函数和查找函数 { //访问u的所有子节点v for each(u,v) { Tarjan(v); //继续往下遍历 union(u,v); //合并v到u上 vis[v] = 1; //标志已遍历 } //访问所有和u有询问关系的e for each(u,e) { if(vis[e]): u,e的最近公共祖先为find(e); } } -
为什么这种思路可行,我的理解是Union会一直动态改变集合的父亲,同时是后序遍历从底向上,可以保证是最近的祖宗节点。
-
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138#include <iostream> #include <vector> #include <numeric> using namespace std; vector<int> parents;//并查集 vector<vector<int>> graph;//邻接表 vector<vector<int>> Question;//问题数组 vector<bool> visited;//判断是否在栈里面 vector<vector<int>> Ret;//返回的uv的最近公共祖先,依次是u,v,ancestor //递归寻找返回父亲id int Find(int idx) { //如果是根节点,直接返回 if (idx == parents[idx]) { return idx; } //递归查找,同时更新父节点, 动态压缩最后树的高度只是2 parents[idx] = Find(parents[idx]); return parents[idx]; } //合并父节点,以等号后面的变量为新的根节点,即依次是v,u void Union(int idx1, int idx2) { int newroot = Find(idx2); //找到idx1的最高的父亲节点,从下往上 parents[Find(idx1)] = newroot; } //u是当前节点 void tarjan(int u) { //询问所以子节点 for (int &v:graph[u]) { tarjan(v); Union(v, u);//第二个是父亲 visited[v] = true; } //询问关系 for (int &e:Question[u]) { if (visited[e]) { //查找公共祖先 int ancestor = Find(e); Ret.push_back({u, e, ancestor}); } } } int main() { int n; cin >> n;//输入树的节点个数 int m; cin >> m;//输入有向边的个数,第一个是第二个的父节点 vector<vector<int>> Link(m); for (int i = 0; i < m; ++i) { int a, b; cin >> a >> b; Link[i].push_back(a); Link[i].push_back(b); } int k;//求最近的祖宗点的询问 cin >> k; vector<vector<int>> Qus(k); for (int i = 0; i < k; ++i) { int a, b; cin >> a >> b; Qus[i].push_back(a); Qus[i].push_back(b); } //逻辑处理 Ret.clear(); parents.resize(n, 0); //初始化并查集 iota(parents.begin(), parents.end(), 0);//从0开始给父亲赋值 visited.resize(n, false); graph.resize(n); Question.resize(n); //初始化图 for (int i = 0; i < m; ++i) { //注意每个数都减1 graph[Link[i][0] - 1].push_back(Link[i][1] - 1); } //初始化问题 for (int i = 0; i < k; ++i) { Question[Qus[i][0] - 1].push_back(Qus[i][1] - 1);//1.两边都要加入 Question[Qus[i][1] - 1].push_back(Qus[i][0] - 1);// } //tarjan算法处理 for (int i = 0; i < n; ++i) { if (!visited[i]) { visited[i] = true;//在这里赋值 tarjan(i); } } //输出 for (int i = 0; i < Ret.size(); ++i) { cout << Ret[i][0]+1 << "--" << Ret[i][1]+1 << " : " << Ret[i][2]+1 << endl; } return 0; } /* 1 2 3 4 5 | 6 7 || 8 输入 8 7 1 2 1 3 2 4 2 5 3 6 4 7 5 8 3 2 5 2 6 7 5 输出 5--7 : 2 2--5 : 2 6--2 : 1 */
LCA 最近公共祖先相关算法
LCA有三种做法:
①DFS序转为线性,RMQ求最小值(在线);
②倍增法;
③tarjan算法,并查集和DFS(离线)。
在线算法是指每次访问都可以立即给出答案,即随时都可以访问。
离线算法是要把所有访问全部记录下来,走的时候得到答案。
欧拉图/半欧拉图
基本理论
-
一笔画问题与欧拉图或者半欧拉图有着紧密的联系,下面给出定义:
-
通过图中所有边恰好一次且行遍所有顶点的通路称为欧拉通路。
-
通过图中所有边恰好一次且行遍所有顶点的回路称为欧拉回路。
-
具有欧拉回路的无向图称为欧拉图。
-
具有欧拉通路但不具有欧拉回路的无向图称为半欧拉图。
-
-
如果没有保证至少存在一种合理的路径,我们需要判别这张图是否是欧拉图或者半欧拉图,具体地:
-
对于无向图 GG,GG 是欧拉图当且仅当 GG 是连通的且没有奇度顶点。
-
对于无向图 GG,GG 是半欧拉图当且仅当 GG 是连通的且 GG 中恰只有 2 个奇度顶点。
-
对于有向图 GG,GG 是欧拉图当且仅当 GG 的所有顶点属于同一个强连通分量且每个顶点的入度和出度相同。
-
对于有向图 GG,GG 是半欧拉图当且仅当 GG 的所有顶点属于同一个强连通分量且
- 恰有一个顶点的出度与入度差为 1;
- 恰有一个顶点的入度与出度差为 1;
- 所有其他顶点的入度和出度相同。
-
Hierholzer算法
-
希尔霍尔策算法——逐步插入回路法
-
问题简述:现给出一个有向图,且为欧拉图。求欧拉回路。
-
Hierholzer 算法过程:
- 选择任一顶点为起点,遍历所有相邻边。
- 深度搜索,访问相邻顶点。将经过的边都删除。
- 如果当前顶点没有相邻边,则将顶点入栈。然后返回。
- 栈中的顶点倒序输出,就是从起点出发的欧拉回路。
- 注:我的理解,当知道哪个是欧拉迹的起点之后,这套算法的效率很高,可以参考下面332的例题。但不知道起点的时候,需要每个顶点都要进行一遍算法,返回条件我认为是stack的size和顶点个数相同。
-
给你一份航线列表
tickets,其中tickets[i] = [fromi, toi]表示飞机出发和降落的机场地点。请你对该行程进行重新规划排序。所有这些机票都属于一个从
JFK(肯尼迪国际机场)出发的先生,所以该行程必须从JFK开始。如果存在多种有效的行程,请你按字典排序返回最小的行程组合。例如,行程
["JFK", "LGA"]与["JFK", "LGB"]相比就更小,排序更靠前。假定所有机票至少存在一种合理的行程。且所有的机票 必须都用一次 且 只能用一次。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33class Solution { public: unordered_map<string, priority_queue<string,vector<string>, std::greater<string>>> dp;//从大到小,表明要逆序,因为题目要求是返回最小的行程组合 vector<string> ret; void dfs(const string &curr)//万能引用 { //节点存在且路径没被删除 while(dp.count(curr) && dp[curr].size()>0){ string temp=dp[curr].top(); //删除路径 dp[curr].pop(); //深度优先搜索 dfs(std::move(temp));//减少拷贝构造,反正temp也要被销毁 } ret.push_back(curr);//用ret.emplace_back(curr)可以减少时间 //ret.emplace_back(curr); } vector<string> findItinerary(vector<vector<string>>& tickets) { ret.clear(); dp.clear(); //初始化哈希映射 for(auto &i:tickets){ dp[i[0]].push(i[1]);//用emplace可以减少时间 //dp[i[0]].emplace(i[1]); } dfs("JFK"); //反转路径 reverse(ret.begin(), ret.end()); return ret; } }; -
有一个需要密码才能打开的保险箱。密码是
n位数, 密码的每一位是k位序列0, 1, ..., k-1中的一个 。你可以随意输入密码,保险箱会自动记住最后
n位输入,如果匹配,则能够打开保险箱。举个例子,假设密码是
"345",你可以输入"012345"来打开它,只是你输入了 6 个字符.请返回一个能打开保险箱的最短字符串。
1 2 3/*解释 当n=1, k=2的时候,就是说密码是1位,可能是0,也可能是1,那么这个答案就应该包含0,也包含1,顺序不要紧,只要按照这答案输入,遇到对的情况自然会打开。继续看n=2, k=2,那么密码就可能是01、10、00、11,密码就应该包含这四种情况,看一下答案,"00110" , "01100", "10011", "11001",是不是这四种答案每个里边都包含这个子串? 再看n=3, k=2,那么密码就应该包含000、001、010、011...等等,可以看一下答案,答案肯定是包含这几个串的:0011101000 */
无向图的连通分量的数量算法
- 有三种方法:深度优先搜索,广度优先搜索,并查集
- 547题